The elf, despite her efforts to sing quietly and not be noticed, sees her charm spell fail miserably. The guard walks past their cell without showing the slightest sign of seduction. Worse still, he seems to realize the elf’s attempt to charm him and raises a suspicious eyebrow. The elf’s cellmates understand that their last escape attempt has failed, and they will remain stuck in this situation for now.
The cell remains hopelessly closed, and the magician, seemingly undisturbed, continues her explanation of the triangular probability distribution, apparently ignoring her companions’ sadness. The dice, it seems, have decided to keep them captive a little longer.
The Law of Two Dice
Magician: My dear friends, now that you have a solid understanding of the discrete uniform distribution, let me tell you about another intriguing distribution, the triangular distribution, which occurs when we roll two six-sided dice and sum the values obtained on their top faces.
Unlike the uniform distribution we discussed earlier, the triangular distribution has a different distribution of probabilities.
For a simple roll of a fair six-sided die, the probability of getting any value from 1 to 6 is evenly distributed, at 1/6 for each result. This constitutes a discrete uniform distribution. However, when we roll two dice and sum the values, the outcomes are no longer evenly distributed but rather follow a triangular distribution.

Sum of dice is 2: Probability 1/36
Sum of dice is 3: Probability 2/36
Sum of dice is 4: Probability 3/36
Sum of dice is 5: Probability 4/36
Sum of dice is 6: Probability 5/36
Sum of dice is 7: Probability 6/36
Sum of dice is 8: Probability 5/36
Sum of dice is 9: Probability 4/36
Sum of dice is 10: Probability 3/36
Sum of dice is 11: Probability 2/36
Sum of dice is 12: Probability 1/36
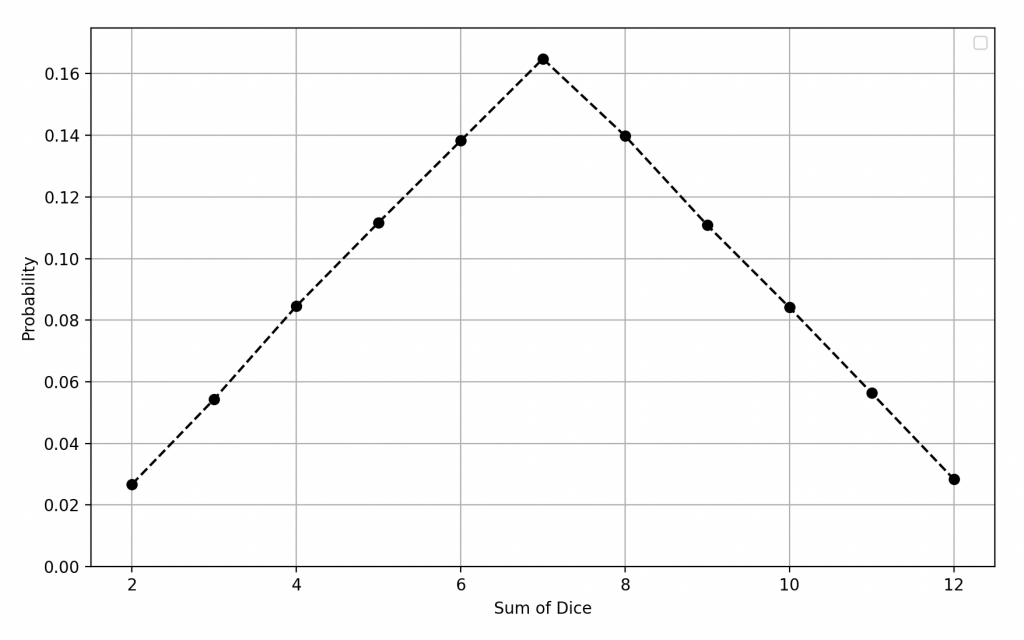
As you can see, the most probable sum is 7, with a probability of 6/36, while the extremes, 2 and 12, have the lowest probability at only 1/36.
There are several possible combinations with two six-sided dice to obtain a specific sum. Let me enumerate them:
– To obtain a sum of 2, there is only one possible combination: 1+1.
– To obtain a sum of 3, there are two possible combinations: 1+2 and 2+1.
– To obtain a sum of 4, there are three possible combinations: 1+3, 2+2, and 3+1.
– And so on, until we reach a sum of 12, which has only one possible combination: 6+6.
This triangular distribution is fascinating because it reflects how probabilities are distributed when we combine the results of two dice. Keep in mind that this knowledge could prove useful in your future adventures, as it will allow you to estimate the chances of success when dealing with situations that involve complex dice rolls.
It's not Over !
However, it’s important to remember that everything that has just been told is not the true ending of the story, but rather a variation of what could have happened.
In the world of role-playing games, the possibilities are endless, and the fate of our adventurers often depends on the players’ choices and the Game Master’s decisions. So, let the quest continue because every adventure is unique and unpredictable, and new challenges await our brave heroes in the dark corners.
Find the true ending.
Bibliography
M. Fréchet, M. Halbwachs, Le calcul des probabilités à la portée de tous, Dunod, 1924, 297 p.
C. Barboianu, Probability Guide to Gambling. The Mathematics of Dice, Slots, Roulette, Baccarat, Blackjack, Poker, Lottery and Sport Bets, INFAROM Publishing, 2006, 316 p
P. Nahin, Digital Dice. Computational Solutions to Practical Probability Problems, Princeton University Press, 2008, 263 p.
I. Stewart, Do Dice Play God?: The Mathematics of Uncertainty, 2019
import matplotlib.pyplot as plt
import numpy as np
# Number of simulations
n_simulations = 100000
# Simulations of rolling two dice and calculating sums
results = np.random.randint(1, 7, size=(n_simulations, 2))
sums = np.sum(results, axis=1)
# Calculation of probability density
unique, counts = np.unique(sums, return_counts=True)
probability = counts / n_simulations
# Creating the probability density plot
plt.figure(figsize=(10, 6))
plt.plot(unique, probability, marker='o', linestyle='--', color='black')
# Labeling axes and adding a title
plt.xlabel('Sum of Dice')
plt.ylabel('Probability')
# Limiting the y-axis scale from 0 to the maximum probability
plt.ylim(0, max(probability) + 0.01)
# Displaying the legend
plt.legend()
# Displaying the plot
plt.grid(True)
plt.show()
