Voleur : (chuchotant) J’ai un mauvais pressentiment à propos de ce levier. On ne sait pas ce qu’il pourrait déclencher.
Ranger : (prudent) Tu as raison, la prudence est de mise dans cette situation. Ne tirons pas ce levier sans avoir plus d’informations.
Ils décident donc de ne pas toucher au levier pour le moment, préférant ne pas risquer une réaction imprévisible. Cependant, à ce moment précis, le temps semble se figer autour d’eux, et l’entité lumineuse dans la cage en verre commence à prendre la parole.
Azar : (d’une voix éthérée) Vous avez fait preuve de sagesse en évitant le levier, mais le temps presse. Une équipe de soldats approche, menée par un puissant mage. Pour triompher de ces ennemis, vous devrez comprendre les subtilités de la loi de probabilité multinomiale.
La Loi des pièces
Le Divin Azar s’éleva, ses paroles chargées de sagesse, pour éclairer les aventuriers sur la loi binomiale, une loi fondamentale en probabilité.

Il expliqua que la loi binomiale reposait sur un nombre n de choix binaires et indépendants, tout comme n lancer d’une pièce de monnaie, où les deux issues possibles étaient Pile ou Face (n étant un nombre quelconque comme 1, 12, 100 etc). Dans le cas d’une pièce équilibrée, la probabilité de Pile, notée \(p_1\), était de 0.5, tandis que la probabilité de Face, notée \(p_2\) (ou \(1-p_1\)), était également de 0.5. De plus, il souligna que si la pièce était biaisée, ces probabilités (\(p_1\) et \(p_2\)) pouvaient prendre d’autres valeurs, telles que 0.4 ou 0.6, révélant ainsi un déséquilibre (voir l’article Toss a Coin to Your Witcher).
En des termes mathématiques, la loi binomiale est une loi de probabilité discrète décrite par deux paramètres qui sont le nombre de lancers n (ou le nombre d’expériences réalisées) et la probabilité de succès \(p_1\) (ça peut aussi être \(p_2\)).
Azar continua son exposé en présentant la formule permettant de calculer la probabilité d’obtenir exactement \(n_1\) Pile et \(n_2\) Face dans une série de n essais. Elle ressemblait à ceci :
\begin{equation*}\mathbb{P}(N_1 = n_1, N_2 = n_2) =\frac{n!}{n_1!n_2!} \cdot p_1^{n_1} \cdot p_2^{n_2}\end{equation*}
ou n! représentait la multiplication de tous les entiers de 1 à n soit \(n!= n\times (n-1)\times\cdots\times 3\times 2\times 1\), par exemple \(4!=4\times 3\times 2\times 1= 24\). Evidemment, à l’école de mathématique cette formule n’est pas la plus commune mais nous n’en parlerons pas ici.
Cependant, il ajouta que cette loi ne permettait pas de déterminer l’ordre dans lequel les résultats étaient apparus (l’ordre ne compte pas).
Pour illustrer son enseignement, il fit appel au chef du groupe, le ranger, qui accepta de lancer une pièce de monnaie cinq fois de suite. Les aventuriers, les yeux rivés sur la pièce en suspension, observèrent avec fascination la séquence finale : PPFPF.
Avec son aura mystique, il expliqua que la probabilité d’obtenir précisément cette séquence était de \(\frac{1}{2^{5}}\), ce qui signifiait qu’il y avait une chance sur 32 que cette séquence se produise. Les aventuriers commençaient à saisir l’importance des calculs de probabilité dans des situations telles que celle-ci.
Azar insista sur le fait que la loi binomiale prenait en compte toutes les manières possibles d’obtenir trois Pile parmi les cinq tirages (soit 20 possibilités), et il rappela la formule correspondante
\begin{equation*}\mathbb{P}(N_1 = 3, N_2=2) =\frac{5!}{3!2!} \cdot p_1^3 \cdot p_2^{2} = 20 \times \frac{1}{2^{5}}\end{equation*}

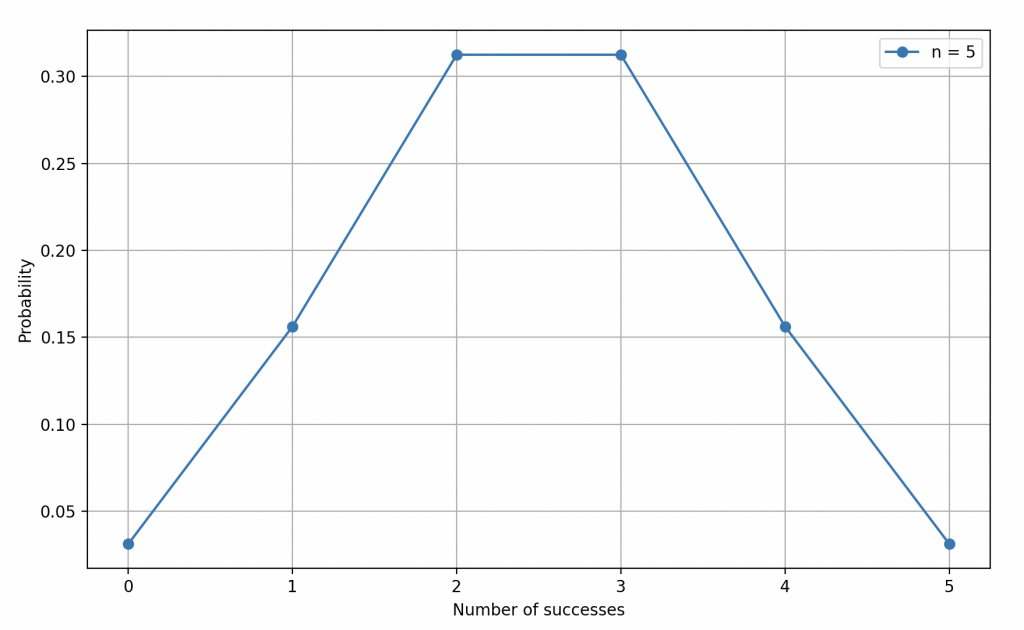
Loi binomiale de paramètres \(n=5\) et \(p_1=0.5\).
Il expliqua ensuite que la loi binomiale avait plusieurs caractéristiques clés essentielles pour comprendre et analyser une expérience donnée.
L’espérance de la loi binomiale, symbolisée par \(\mathbb{E}(N_1)\), fut définie comme la valeur attendue du nombre de succès dans n essais, en fonction de la probabilité \(p_1\) de succès dans un essai individuel :
\begin{equation*}\mathbb{E}(N_1) = n \cdot p_1 = 0.5\times n\end{equation*}
Azar ajouta que la variance de la loi binomiale se calculait comme suit, permettant de quantifier la dispersion des résultats autour de l’espérance et offrant un aperçu de la stabilité ou de la variabilité des résultats :
\begin{equation*}V(N_1) = n \cdot p_1 \cdot p_2 = 0.25\times n\end{equation*}
Azar éclaira ensuite les aventuriers sur le mode de la loi binomiale en expliquant que le mode était la valeur de \(n_1\) qui maximisait la probabilité. Pour une pièce équilibrée, il souligna que le mode était situé à \(\frac{n}{2}\), ce qui signifiait que le résultat le plus probable était d’obtenir autant de Pile que de Face.
Il mentionna également l’asymétrie et le kurtosis de la loi binomiale, reconnaissant que les calculs pouvaient être plus complexes que les précédents.
L’asymétrie, notée \(\gamma_1(N_1)\) , fut définie comme une mesure de l’asymétrie de la loi binomiale, avec la formule suivante :
\begin{equation*}\gamma_1(N_1) = \frac{p_2-p_1}{\sqrt{np_1p_2}}=0\end{equation*}
Clairement, lorsque la pièce est équilibrée, nous obtenons une courbe symétrique par rapport à la valeur moyenne.
Quant au kurtosis, symbolisé par \(\gamma_2(N_1)\), il évaluait la forme de la distribution par rapport à une loi normale standard (courbe en cloche), avec la formule suivante :
\begin{equation*}\gamma_2(N_1) = \frac{1-6p_1p_2}{np_1p_2}\end{equation*}
Une remarque importante à prendre en compte est que plus le nombre de lancers est grand plus la loi binomiale se rapproche d’une loi que l’on appelle loi normale (courbe en cloche). Cela peut s’avérer utile dans la modélisation de phénomènes réels, car la loi normale est une distribution couramment observée dans la nature (Nous l’étudierons en détail dans un prochain article).
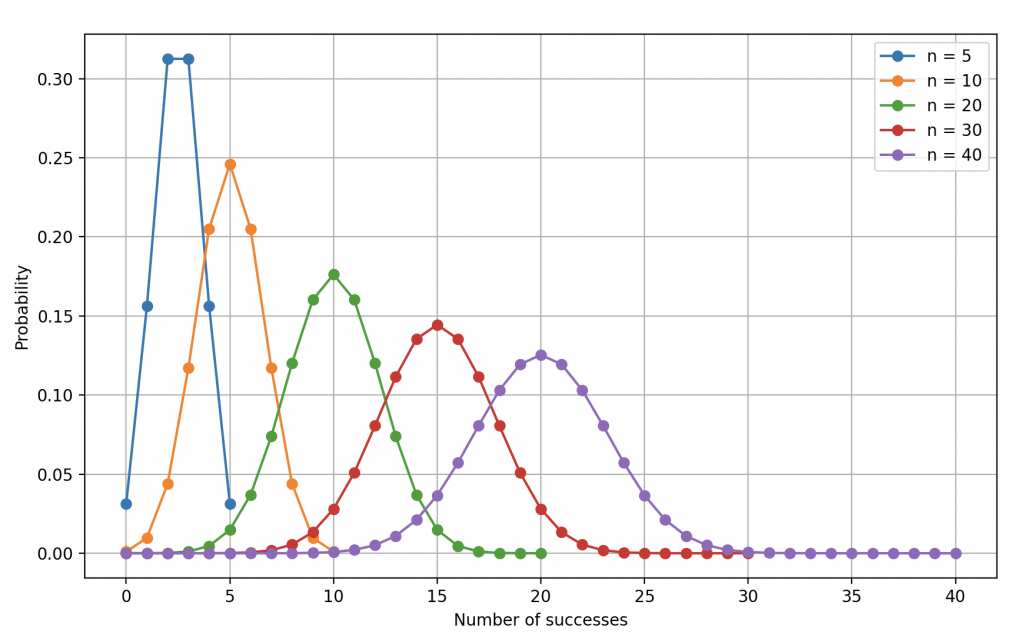
Loi binomiale de paramètres \(n=5,10,20,30,40\) et \(p_1=0.5\).

Le divin conclut en soulignant que la loi binomiale était un outil essentiel pour modéliser des expériences binaires avec des probabilités de succès et d’échec. Les caractéristiques tels que l’espérance, la variance, le mode, l’asymétrie et le kurtosis étaient autant d’outils pour analyser la distribution des résultats possibles, aidant ainsi les aventuriers à prendre des décisions éclairées dans leurs quêtes futures.
La Loi des Dés
Le moment redouté approchait. Quatre soldats, défenseurs acharnés de leur garnison, s’avançaient pour faire face à nos courageux héros. Pour triompher de ces adversaires redoutables, il allait falloir faire appel à la puissance de leurs dés magiques et exécuter de bons tirages.
Soldat 1 : 3 fois le nombre 6, 1 fois le nombre 5, 0 fois le nombre 4, 1 fois le nombre 3, 1 fois le nombre 2 et 1 fois le nombre 1.
Soldat 2: 0 fois le nombre 6, 1 fois le nombre 5, 3 fois le nombre 4, 0 fois le nombre 3, 1 fois le nombre 2 et 2 fois le nombre 1.
Soldat 3: 2 fois le nombre 6, 1 fois le nombre 5, 1 fois le nombre 4, 1 fois le nombre 3, 1 fois le nombre 2 et 1 fois le nombre 1.
soldat 4: 1 fois le nombre 6, 1 fois le nombre 5, 1 fois le nombre 4, 1 fois le nombre 3, 3 fois le nombre 2 et 0 fois le nombre 1.
Mage : 7 fois le nombre 6, 0 fois le nombre 5, 0 fois le nombre 4, 0 fois le nombre 3, 0 fois le nombre 2 et 0 fois le nombre 1.
Dans cette situation, la complexité résidait dans le fait qu’au lieu d’avoir seulement deux choix possibles, comme dans un simple lancer de pièce, ils avaient maintenant six résultats possibles, et cela pouvait varier en fonction des circonstances, parfois plus, parfois moins (cela dépends des dés que vous utilisez).
Azar : (d’une voix apaisante) Pour vous permettre de mieux saisir prenez uniquement un dé à six faces. Comme les dés ne sont pas pipés, la probabilité d’obtenir un 6, que nous noterons \(p_6\) est la même que celle d’obtenir un 1 (et que toutes les autres) soit \(p_1\) et valent 1/6. Ainsi, tout se passe comme dans le cas d’un lancer de pièce équilibrée, où chaque résultat a la même probabilité de se produire. (la loi uniforme discrète.)
Azar poursuivit par analogie avec la loi binomiale, pour un dé quelconque, la probabilité d’avoir \(n_6\) valeurs 6, \(\cdots\), \(n_1\) valeurs 1 parmi n tirages d’un dé vaut
\begin{equation*}
\mathbb{P}(N_6=n_6, \cdots, N_1=n_1) =\frac{n!}{n_6!n_5!n_4!n_3!n_2!n_1!} \cdot p_1^{n_1} \cdot p_2^{n_2}\cdot p_3^{n_3}\cdot p_4^{n_4}\cdot p_5^{n_5}\cdot p_6^{n_6}
\end{equation*}
et pour un dé équilibré, cela se simplifie en :
\begin{equation*}
\mathbb{P}(N_6=n_6, \cdots, N_1=n_1) =\frac{n!}{n_6!n_5!n_4!n_3!n_2!n_1!} \cdot\left(\frac{1}{6}\right)^n
\end{equation*}
Cette formule prenait en compte le nombre de façons de réarranger les résultats des dés pour chaque tirage, ainsi que les probabilités d’obtenir chaque face. Dans le cas d’un dé équilibré, cette formule se simplifiait en utilisant la probabilité 1/6 pour chaque face.
Azar mit ensuite en application ces concepts mathématiques pour expliquer que la probabilité de vaincre le soldat 1 était très faible, calculée à environ 0,003. Nos héros restaient perplexes, réalisant que leurs chances de succès étaient minces.
\begin{equation*}\mathbb{P}(N_6=3, N_5 = 1, N_4 = 0, N_3 = 1, N_2 = 1, N_1=1)=\frac{7!}{3!1!0!1!1!1!}\cdot\left( \frac{1}{6}\right)^7\approx0,003\end{equation*}
Faisant face à leur destin, les aventuriers lancèrent les dés, espérant obtenir la séquence magique. Incroyablement, ils réussirent à battre le premier soldat en obtenant la séquence 1, 6, 6, 6, 5, 2, 3, une combinaison qui avait une chance infime de se produire, soit seulement 1 chance sur 279936, comme toutes les configurations possibles à 7 lancers.
Azar ne mentionna pas énormément les propriétés d’une telle loi, seulement les plus classiques l’espérance et la variance qui ont les mêmes formulations que pour la loi binomiale. Il n’enseigna pas non plus sa représentation graphique puisque l’humanité ne peut pas se représenter facilement des courbes à plus de 3 dimensions. Ici, il y en a 6 ! Il fallait donc seulement s’accommoder de la représentation de la binomiale et avoir un peu d’imagination.
Nos héros avaient triomphé d’un premier obstacle, mais la route qui s’offrait à eux restait longue et semée d’incertitudes. Ils avaient maintenant saisi l’importance cruciale de la probabilité et de la loi multinomiale dans leur quête. Armés de ces connaissances puissantes, ils se préparaient à affronter les soldats restants avec une détermination inébranlable et une lueur d’espoir dans les yeux. La bataille était loin d’être gagnée, mais ils étaient prêts à faire face à l’incertitude qui les attendait.
Cependant, malgré leur maîtrise des probabilités, nos aventuriers n’étaient pas invincibles. Leur périple les conduisit finalement au mage, dont les probabilités de défaite étaient encore plus minces. Le sort en décida ainsi, et nos héros furent vaincus par le mage, malgré leur bravoure et leur connaissance des lois de la probabilité.
Tromperie!
Alors que nos héros se laissaient emporter par les mystères de leur destin, Azar leur révéla une vérité profonde : l’ordre des événements n’avait pas d’importance fondamentale, contrairement à la série improbable de coïncidences qui les avait guidés jusqu’à lui (Il leur conseillait ainsi de calculer quel avait été la probabilité d’arriver jusqu’à lui sans mourir). Ces circonstances fortuites avaient forgé leur destin de manière inattendue, comme si le fil du récit s’était tissé avec les fils du hasard.
C’était comme si tout ce périple n’avait été qu’un jeu, un jeu qui avait débuté lorsque le voleur avait lancé cette pièce au nain dans la taverne. Chaque jet de dé dans la cellule, chaque coup de dés face aux soldats, tout avait contribué à sculpter leur destin, les menant inexorablement à Azar. La réalité et la fiction s’étaient entrelacées, créant une aventure palpitante où la probabilité était devenue le fil conducteur.
Nos héros, dans un mélange d’amusement et de réflexion, se remémorèrent les leçons des loi de probabilité, réalisant à quel point la compréhension de tels concepts pouvait influencer le cours de leur histoire. Ils savourèrent leur retour, conscient que, même dans le récit de leur vie, le hasard avait sa propre place, tissant une trame complexe et captivante.
Bibliographie
P. Bogaert, Probabilités pour scientifiques et ingénieurs : Introduction au calcul des probabilités, De Boeck Supérieur, 2005, 402 p
E. Gossett, Discrete Mathematics with Proof, Hoboken (N.J.), John Wiley & Sons, 2009, 904 p
E. Lesigne, Heads or tails : an introduction to limit theorems in probability, Providence (R.I.), AMS, 2005, 150 p.
D. Foata, A. Fuchs et J. Ranchi, Calcul des probabilités : Cours, exercices et problèmes corrigés, Paris/Berlin/Heidelberg etc., Dunod, 2012, 3e éd., 368 p.
import matplotlib.pyplot as plt
import scipy.stats as stats
# Parameters of the binomial distribution
p = 0.5 # Probability of success
n_values = [5, 10, 20, 30, 40] # Different values of n
# Create the graph
plt.figure(figsize=(10, 6))
# Simulation and plotting of curves for each value of n
for n in n_values:
x = range(n + 1)
y = [stats.binom.pmf(k, n, p) for k in x]
plt.plot(x, y, marker='o', label=f'n = {n}')
# Labeling of axes and adding a title
plt.xlabel('Number of successes')
plt.ylabel('Probability')
# Display the legend
plt.legend()
# Display the graph
plt.grid(True)
plt.show()
