Les Stormtroopers sont mauvais en tir ? Oui.
Par Jordan Moles le 23 Juillet, 2023

La Méthode Monte Carlo
La méthode de Monte Carlo est une stratégie mathématique efficace utilisée pour approximer des résultats autrement impossibles à calculer avec précision. Elle repose sur l’utilisation de nombres pseudo-aléatoires pour simuler des événements aléatoires et en déduire des résultats probables. Une illustration simple pour comprendre cette méthode serait d’imaginer une armée de stormtroopers tirant aléatoirement sur une cible. Grâce à la méthode de Monte Carlo, nous pouvons estimer le taux de précision des stormtroopers en simulant leur tir aléatoire et en comptant le nombre de tirs qui atteignent la cible. Mais surtout, cette méthode leur permet d’estimer des aires.
Cette méthode repose sur la loi des grands nombres, qui affirme que si un grand nombre d’expériences aléatoires indépendantes sont réalisées, la fréquence des résultats convergera vers la probabilité théorique. Par exemple, si vous lancez une pièce de monnaie équilibrée un très grand nombre de fois, elle apparaîtra pile ou face la moitié du temps. Pour utiliser cette méthode, il faut d’abord définir un espace de simulation d’événements aléatoires, générer des nombres pseudo-aléatoires pour imiter ces événements, et compter le nombre d’occurrences qui se produisent dans une région spécifique d’intérêt. Ces informations sont ensuite utilisées pour estimer la probabilité qu’un événement particulier se produise.
Par exemple, pour estimer le taux de précision des stormtroopers, nous pourrions définir un espace de simulation qui représente la cible, les laisser tirer, et compter le nombre de tirs qui touchent la cible. En utilisant le rapport entre le nombre de tirs qui touchent la cible et le nombre total de tirs, nous pouvons estimer le taux de précision des stormtroopers. Pour ce faire,
1. Placez un stormtrooper dans le vaste stand de tir fermé.
2. Dessinez un cercle de rayon de 25 mètres au centre du mur arrière carré de 50 mètres.
3. Maintenant, il est temps d’ordonner au stormtrooper d’ouvrir le feu.
« Stormtrooper, attention, cible en vue sur le mur arrière, tirez mille coups ! »

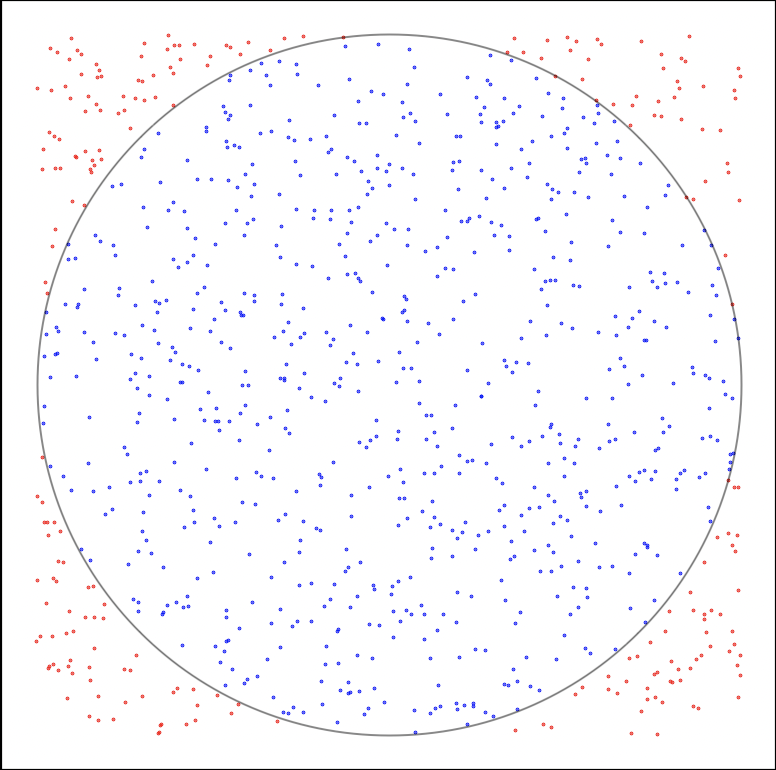
Figure 1: Un stormtrooper essayant de tirer sur la cible et le résultat obtenu avec mille tirs.
Estimation de π et de la Surface du Faucon Millennium
Avant de continuer, rappelons que l’aire d’un carré de côté R est \(S_{carré}=R²\) et l’aire d’un cercle de rayon R est \(S_{cercle}=π R²\). Nous commencerons par l’estimation la plus simple : celle de π. Cela fonctionne en utilisant les mêmes étapes décrites précédemment.
1. Mettez l’armée d’un million de stormtroopers identiques dans le grand stand de tir clos.
2. Dessinez un cercle de rayon 25 mètres à l’intérieur du mur arrière carré de 50 mètres.
3. Rappelez-vous l’ordre.
« Stormtroopers, attention, cible sur le mur arrière en vue, tirez un coup. »
1. Comptez le nombre d’impacts (ou de points) qui tombent à l’intérieur du cercle.
2. Utilisez la proportion d’impacts à l’intérieur du cercle par rapport au nombre total d’impacts générés pour estimer π. Plus précisément, vous pouvez utiliser la formule suivante :

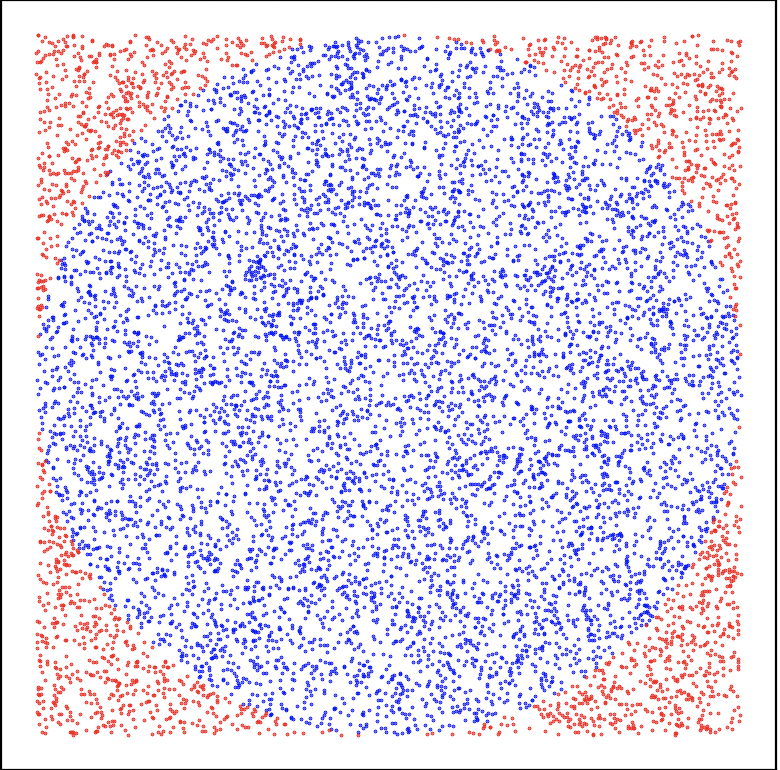
Figure 2: L'armée est arrivée et a lancé les premiers 10 000 tirs.
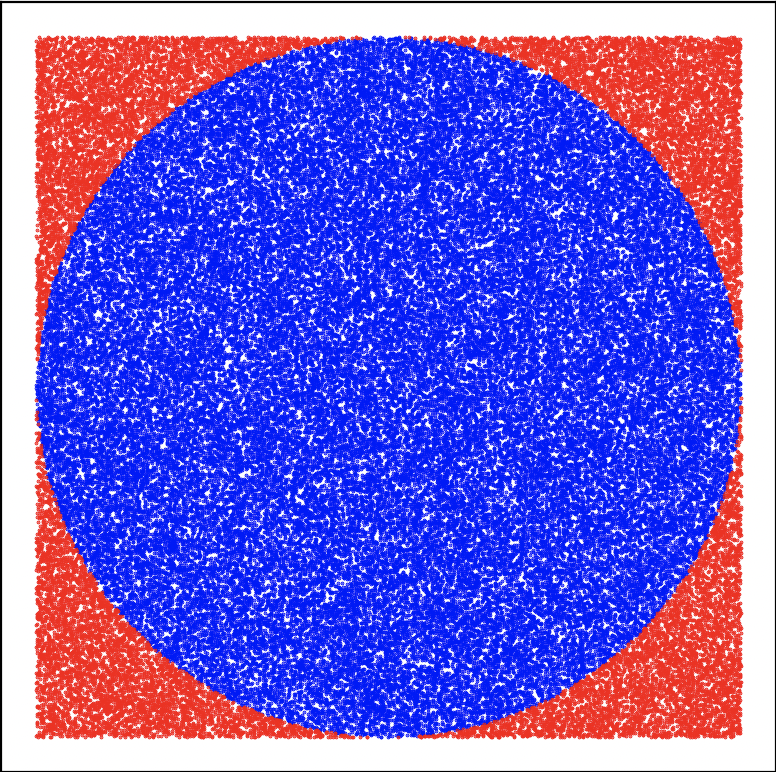

Figure 3: De gauche à droite : 100 000 tirs et 1 million de tirs.


Figure 4: Voici la photo réelle du vaisseau spatial et le plan.
La méthodologie sera presque la même. Nous utilisons une simulation informatique où les stormtroopers tirent aléatoirement à la surface du vaisseau spatial. Chaque point où un « stormtrooper » touche la surface est enregistré et la surface totale est ensuite calculée en comptant le nombre total de points et en le comparant à la taille totale de la surface du vaisseau spatial. Cette méthode est très efficace car elle prend en compte les formes irrégulières de la surface du vaisseau spatial, ce qui rendrait difficile une estimation de surface plus traditionnelle. Cependant, malheureusement, cela conduira à la destruction totale du vaisseau spatial !
1. Placez l’armée de stormtroopers dans un stand de tir fermé et immense.
2. Tracez un rectangle de 35 mètres sur 25 mètres pour représenter la surface du mur arrière et collez le Faucon Millennium dessus.
3. Ordonnez aux stormtroopers d’ouvrir le feu.
4. Comptez le nombre de tirs qui atteignent la surface du Faucon Millennium.
5. Utilisez la proportion de tirs qui atteignent la surface du Faucon Millennium par rapport au nombre total de tirs pour estimer la surface du Faucon Millennium. Plus précisément, vous pouvez utiliser la formule suivante :
\begin{equation*}
\text{Surface du Faucon Millennium}=35\times 25\frac{\text{Nombre de tirs qui touchent le Faucon Millennium}}{\text{Nombre total de tirs}}.
\end{equation*}
6. Répétez ces étapes plusieurs fois ou augmentez le nombre de stormtroopers pour obtenir une estimation plus précise de la surface du Faucon Millennium.



Figure 5: De gauche à droite, avec 10 000, 100 000 et 1 million de tirs.
La précision de la méthode de Monte Carlo pour estimer les aires dépend du nombre de tirs générés de manière aléatoire. Plus vous effectuez de tirs, plus votre estimation sera précise.
Cependant, il est important de noter que même si vous générez un grand nombre de tirs, vous ne pourrez jamais calculer la valeur exacte de l’aire que vous considérez. Par exemple, avec 1 million de stormtroopers, vous pouvez obtenir une estimation de π avec une précision d’environ 2 décimales. Pour l’aire du Faucon Millenium, nous obtenons approximativement 400,855 m².
L’importance du Manque de Précision
La méthode de Monte Carlo repose fortement sur la génération de nombres aléatoires pour simuler des événements aléatoires. C’est là que le manque de précision des stormtroopers entre en jeu. Dans l’exemple précédent, le manque de précision des stormtroopers dans le tir représente l’aléatoire nécessaire pour que la méthode de Monte Carlo fonctionne de manière efficace (ici, ils tirent parfaitement mal). Sans cette aléa, la méthode ne serait pas en mesure d’approximer les résultats de manière précise.
Laissez-moi vous expliquer ce concept en introduisant Han Solo, un tireur d’élite hautement qualifié, dans la simulation. La distribution des tirs ne serait plus uniformément aléatoire, mais plutôt pondérée vers les zones où Han Solo vise. Plus précisément, si nous estimons sa précision de la même manière que nous l’avons fait avec les stormtroopers, nous constatons qu’il tire presque parfaitement bien.

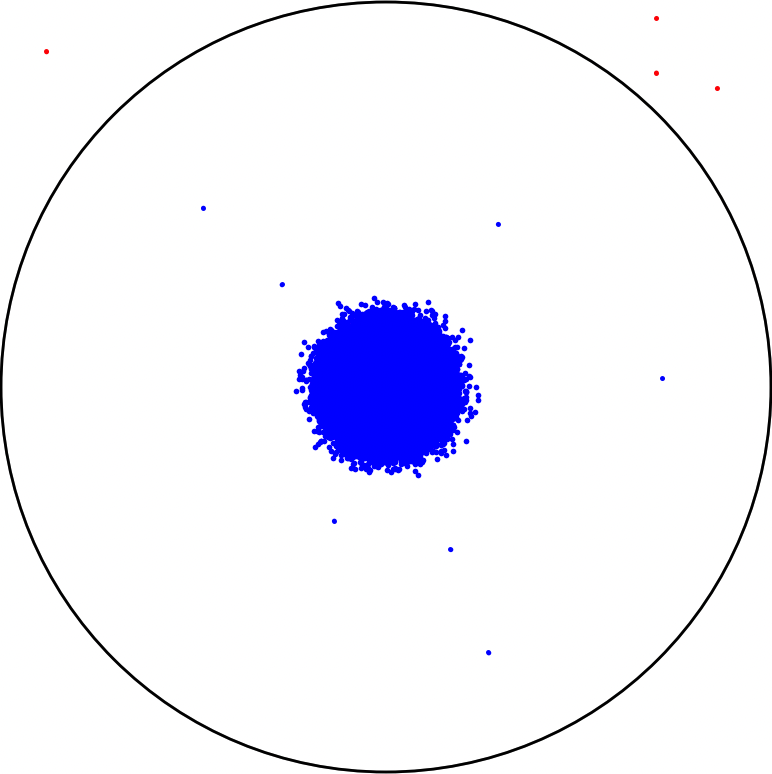
Figure 6: Han solo tirant 1 million de fois.
Peut-être que Chewbacca le dérange ou qu’il a de la poussière dans l’œil, et c’est pourquoi son taux de précision n’est pas de 100 % (c’est ce qu’il dit). Maintenant, à quel point est-il bon pour estimer π ? En utilisant la même formule
\begin{equation*}
\pi=\frac{\text{Nombre d’impacts dans le cercle}}{\text{Nombre total d’impacts}},
\end{equation*}
Il semble que π soit plus ou moins égal à 4 avec 1 million de tirs.
Cela met en évidence une considération importante lors de l’utilisation de la méthode de Monte Carlo – la précision des résultats dépend fortement du caractère aléatoire de la simulation. L’introduction de biais ou de distributions non uniformes peut grandement influencer l’efficacité de la méthode. En termes simples, cela signifie que pour être précis, les nombres aléatoires générés doivent être véritablement aléatoires et ne pas suivre de schéma prévisible ou être précis.
Generation de Nombres Aléatoires
Générer des nombres aléatoires est une tâche fondamentale dans de nombreux domaines, allant de l’informatique à la cryptographie et aux simulations. Bien que nous pensons souvent que le hasard est quelque chose qui se produit naturellement, comme le lancer d’un dé ou le tirage au sort d’une pièce de monnaie, de nombreux nombres aléatoires utilisés en informatique sont en réalité générés par le biais d’algorithmes sophistiqués ou de phénomènes physiques.
Un des méthodes largement utilisées est le générateur de nombres pseudo-aléatoires, qui produit une séquence de nombres qui semble aléatoire, mais qui est en réalité calculée de manière déterministe à partir d’une valeur initiale appelée « graine ». Bien qu’ils ne soient pas véritablement aléatoires, les générateurs pseudo-aléatoires sont très efficaces et suffisamment imprévisibles pour répondre aux besoins pratiques. Cependant, ils peuvent être sujets à des périodicités et des corrélations dans les séquences produites, ce qui peut poser des risques de sécurité dans certaines applications. En utilisant l’analogie de Star Wars, cela revient à prendre un tireur d’élite impérial parfait qui suit un schéma de tir ; il vous suffit d’ordonner le premier tir réussi et chaque tir suivant sera une fonction définie du précédent.

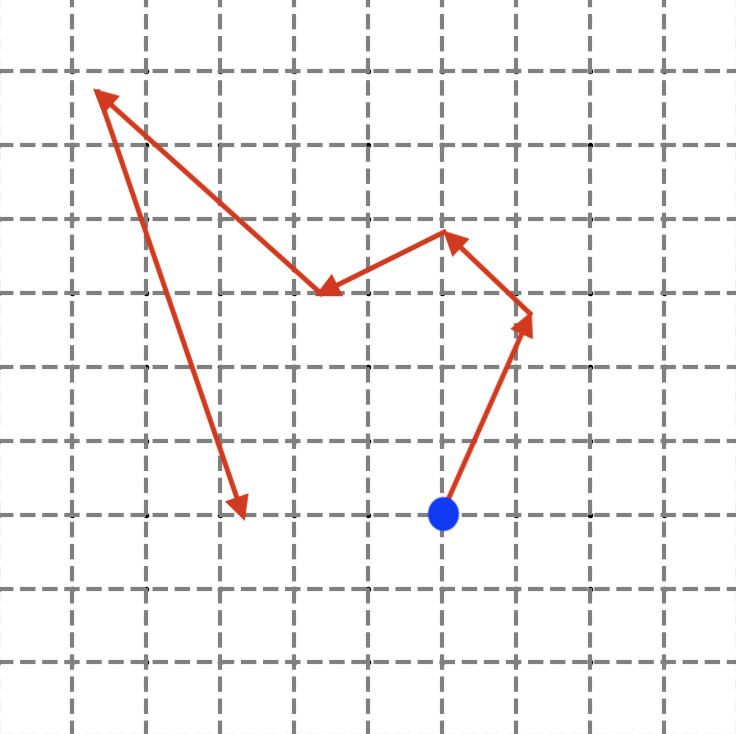
Figure 7: Un tireur d'élite impérial avec une partie de son schéma de tir.
Maintenant, imaginez que vous êtes un espion rebelle et que vous souhaitez envoyer un message secret à votre base. Pour cela, vous avez besoin d’un nombre aléatoire qui servira de clé de chiffrement. Vous pourriez utiliser un générateur de nombres pseudo-aléatoires pour en créer un, mais il y a toujours un risque que l’Empire ait pu prédire la séquence de nombres que vous allez utiliser. Pour vous assurer que votre clé de chiffrement est vraiment aléatoire, vous pourriez utiliser un générateur de nombres quantiques.
Dans cet exemple, le générateur de nombres pseudo-aléatoires serait semblable à un soldat de l’Empire qui suit un plan d’attaque prédéfini et facilement prévisible, tout comme le sniper impérial. D’un autre côté, le générateur de nombres quantiques serait semblable à un scientifique rebelle qui exploite les propriétés uniques des sabres laser pour trouver des solutions imprévisibles à chaque situation. Comme les nombres quantiques sont générés à partir de phénomènes quantiques imprévisibles tels que la polarisation, la phase ou la fréquence des photons, l’Empire ne peut pas prédire la séquence de nombres que vous allez utiliser, rendant votre message secret beaucoup plus sûr. Ces générateurs produisent des nombres vraiment aléatoires et impossibles à reproduire. Bien que encore relativement nouveaux et coûteux, les générateurs de nombres quantiques offrent de grandes perspectives pour des applications nécessitant les plus hauts niveaux de sécurité et d’imprévisibilité.
La Polyvalence et la Puissance de la Méthode de Monte Carlo
En résumé, la méthode de Monte Carlo est une technique mathématique polyvalente et puissante qui permet d’approximer des résultats complexes difficiles à calculer précisément autrement. L’utilisation de nombres aléatoires ou pseudo-aléatoires pour simuler des événements aléatoires et déterminer des résultats probabilistes en fait un outil efficace pour diverses applications, comme en témoignent les simulations des tirs des stormtroopers. Les applications de cette méthode vont au-delà de l’estimation de constantes mathématiques et de l’aire de formes irrégulières, pour inclure la prédiction des résultats d’élections, la simulation de la croissance de la population et l’estimation de la probabilité d’obtenir un certain nombre lors d’un jeu de dés.
La méthode de Monte Carlo est un outil précieux pour de nombreux domaines tels que la physique, l’ingénierie et la finance, en faisant ainsi un élément essentiel de la boîte à outils du mathématicien et du statisticien.

Bibliographie
M. Kalos, P. Whitlock, Monte Carlo Methods, 2008.
D. P. Kroese, T. Taimre, Z.I. Botev, Handbook of Monte Carlo Methods, 2011.
D. P. Kroese, T. Brereton, T. Taimre, Z.I. Botev, Why the Monte Carlo method is so important today, 2014.
S. Weinzierl, Introduction to Monte Carlo methods, 2000.
import random
import matplotlib.pyplot as plt
def estimate_pi(n):
num_points_circle = 0
num_points_total = 0
circle_x, circle_y = [], []
square_x, square_y = [], []
# Loop for generating random points and estimating π
for _ in range(n):
x = random.uniform(-1, 1)
y = random.uniform(-1, 1)
distance = x**2 + y**2
if distance <= 1:
num_points_circle += 1
circle_x.append(x)
circle_y.append(y)
else:
square_x.append(x)
square_y.append(y)
num_points_total += 1
# Plotting the points on a graph
plt.figure(figsize=(5, 5))
plt.scatter(circle_x, circle_y, color='blue', s=0.1)
plt.scatter(square_x, square_y, color='red', s=0.1)
plt.xlim(-1.1, 1.1)
plt.ylim(-1.1, 1.1)
plt.title("Estimation of π using the Monte Carlo method\nN = {}".format(n))
plt.show()
# Calculating and returning the estimated value of π
return 4 * num_points_circle / num_points_total
print(estimate_pi(10000))
import cv2
import numpy as np
import random
# Load the image and convert it to grayscale
img = cv2.imread("/Users/.../falcon2.png", cv2.IMREAD_GRAYSCALE)
# Apply thresholding to get a binary image
ret, thresh = cv2.threshold(img, 127, 255, cv2.THRESH_BINARY)
# Invert the colors so that black becomes white and vice versa
thresh = cv2.bitwise_not(thresh)
# Find contours in the image
contours, hierarchy = cv2.findContours(thresh, cv2.RETR_EXTERNAL, cv2.CHAIN_APPROX_SIMPLE)
# Create a black image to draw the contours
contour_img = np.zeros((img.shape[0], img.shape[1], 3), np.uint8)
# Draw the contours in white on the black image
cv2.drawContours(contour_img, contours, -1, (255, 255, 255), 2)
# Get the size of the image in pixels
height, width = img.shape[:2]
# Retrieve the size of the image in pixels
size = img.shape[:2]
# Define the real dimensions of the Millennium Falcon
real_length = 35 # in meters
real_width = 25 # in meters
# Define the resolution of the image in pixels/meter
resolution = 144
# Calculate the total number of pixels of the ship's surface
total_surface_pixels = int(real_length * real_width * resolution**2)
# Number of random points to generate for the estimation
n = 1000000
# Number of points inside the black figure
num_points_inside = 0
# Generate random points in the image and count the number of points inside the black figure
for i in range(n):
# Generate a random point in the image
x = random.randint(0, width-1)
y = random.randint(0, height-1)
# Check if the point is inside the black figure
if cv2.pointPolygonTest(contours[0], (x, y), False) == 1:
num_points_inside += 1
# Draw the point in blue
cv2.circle(contour_img, (x, y), 1, (255, 0, 0), -1)
else:
# Draw the point in red
cv2.circle(contour_img, (x, y), 1, (0, 0, 255), -1)
# Estimation of the area of the black figure using the Monte Carlo method
estimated_area = (num_points_inside / n) * (width * height)
# Display the image with points in blue and red
cv2.imshow('Image with points', contour_img)
# Wait for the user to press a key to close the window
cv2.waitKey(0)
cv2.destroyAllWindows()
# Display the estimated area of the black figure
print("Estimated area of the black figure:", estimated_area)
import random
import math
import matplotlib.pyplot as plt
num_shots = 1000000
circle_hits = 0
square_hits = 0
circle_x = []
circle_y = []
square_x = []
square_y = []
for i in range(num_shots):
x = random.gauss(0, 0.05) # shots centered at the circle's center
y = random.gauss(0, 0.05)
distance = math.sqrt(x**2 + y**2)
if distance <= 1:
circle_hits += 1
circle_x.append(x)
circle_y.append(y)
else:
square_x.append(x)
square_y.append(y)
square_hits += 1
if random.random() < 0.1: # 10% chance of shooting in the circle
if distance <= 1:
circle_hits -= 1
circle_x.pop()
circle_y.pop()
else:
circle_hits += 1
circle_x.append(x)
circle_y.append(y)
square_hits -= 1
pi_estimation = 4 * circle_hits / square_hits
print("Estimation of pi:", pi_estimation)
fig, ax = plt.subplots(figsize=(6, 6))
ax.set_xlim([-1.2, 1.2])
ax.set_ylim([-1.2, 1.2])
ax.set_aspect('equal')
ax.scatter(square_x, square_y, color='red', s=1, label='Outside the circle')
ax.scatter(circle_x, circle_y, color='blue', s=1, label='Inside the circle')
circle = plt.Circle((0, 0), 1, color='black', fill=False)
ax.add_artist(circle)
ax.legend()
plt.show()
Pour trouver la surface du Faucon Millenium, nous avons utilisé l'image suivante.

