Los Stormtroopers Son Malos en Disparar? Sí.
Por Jordan Moles el 23 de Julio, 2023

El Método Monte Carlo
La técnica de Monte Carlo es una estrategia matemática eficiente que se utiliza para aproximar resultados que de otro modo serían difíciles de calcular con precisión. Se basa en el uso de números pseudoaleatorios para simular eventos aleatorios y obtener resultados probables. Una ilustración simple para comprender este método sería imaginar a un ejército de stormtroopers disparando al azar a un objetivo. Gracias al método de Monte Carlo, podemos estimar la precisión de los stormtroopers simulando sus disparos aleatorios y contando la cantidad de disparos que impactan en el objetivo. Pero sobre todo, esta técnica les permite estimar áreas.
Este método se basa en la ley de los grandes números, que afirma que si se realizan un gran número de experimentos aleatorios e independientes, la frecuencia de los resultados convergerá hacia la probabilidad teórica. Por ejemplo, si lanzamos una moneda equilibrada un gran número de veces, caerá cara o cruz la mitad del tiempo. Para utilizar este método, primero se debe definir un espacio de simulación de eventos aleatorios, generar números pseudoaleatorios para imitar estos eventos y contar la cantidad de ocurrencias que se producen en una región específica de interés. Esta información se utiliza luego para estimar la probabilidad de que ocurra un evento particular.
Por ejemplo, para estimar la precisión de los stormtroopers, podríamos definir un espacio de simulación que represente el objetivo, permitirles disparar y contar la cantidad de disparos que impactan en el objetivo. Utilizando la proporción entre la cantidad de disparos que impactan en el objetivo y el total de disparos, podemos estimar la precisión de los stormtroopers. Para hacer esto,
1. Coloquen un stormtrooper en el amplio stand de tiro cerrado.
2. Dibuja un círculo de radio de 25 metros en el centro de la pared trasera cuadrada de 50 metros.
3. Ahora es el momento de ordenar al stormtrooper que abra fuego.
«Stormtrooper, ¡atención! ¡Objetivo a la vista en el muro trasero, dispare mil veces!»

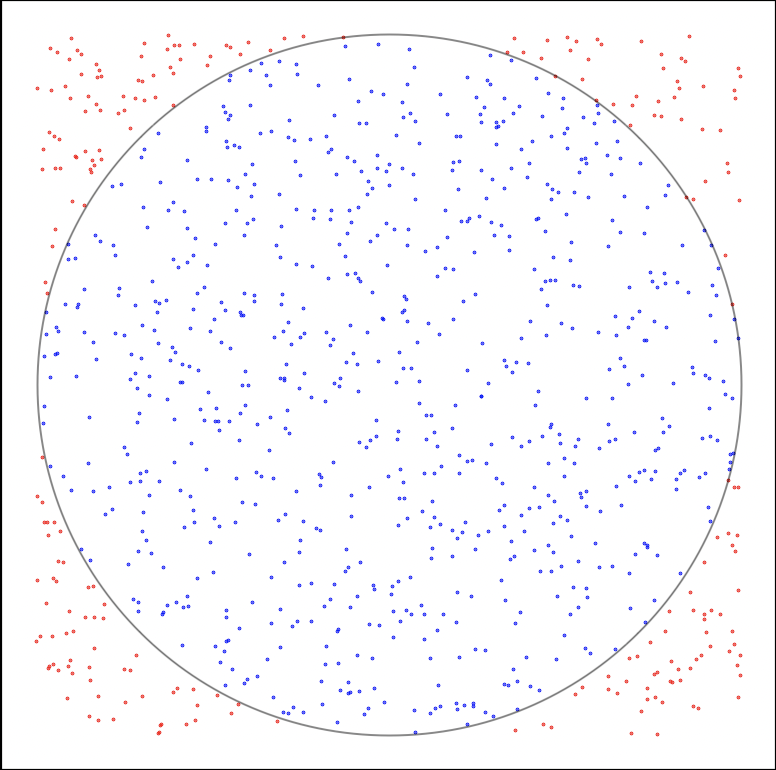
Figura 1: Un stormtrooper intentando disparar a la cible y el resultado obtenido con mil tiros.
Estimación de π y la Superficie del Millenium Falcon
Antes de continuar, recordemos que el área de un cuadrado de lado R es \(S_{cuadrado}=R²\) y el área de un círculo de radio R es \(S_{círculo}=π R²\). Comenzaremos con la estimación más simple: la de π. Esto funciona utilizando los mismos pasos descritos anteriormente.
1. Coloca al ejército de un millón de stormtroopers idénticos en el amplio stand de tiro cerrado.
2. Dibuja un círculo de radio 25 metros dentro del muro trasero cuadrado de 50 metros.
3. Recuerda la orden.
«Stormtroopers, atención, objetivo en el muro trasero a la vista, disparen un tiro.»
1. Cuenta el número de impactos (o puntos) que caen dentro del círculo.
2. Utiliza la proporción de impactos dentro del círculo con respecto al número total de impactos generados para estimar π. Específicamente, puedes usar la siguiente fórmula:
\begin{equation*} \pi=\frac{S_{círculo}}{S_{cuadrado}}=\frac{\text{ El número de impactos dentro del círculo}}{\text{ El número total de impactos}}. \end{equation*} Repita los pasos varias veces o aumente su ejército para obtener una estimación más precisa de π.

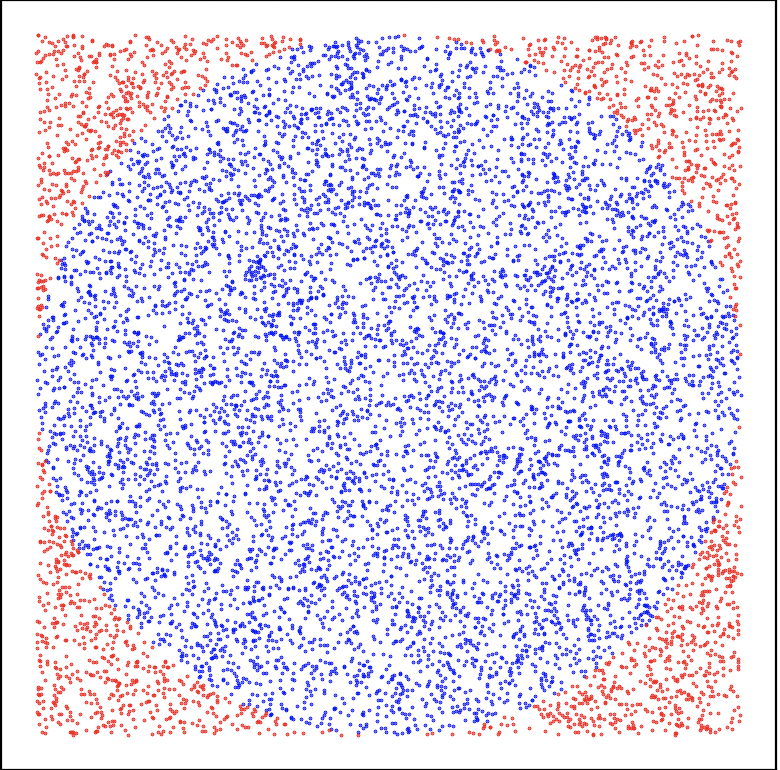
Figura 2: El ejército ha llegado y ha realizado los primeros 10,000 disparos.
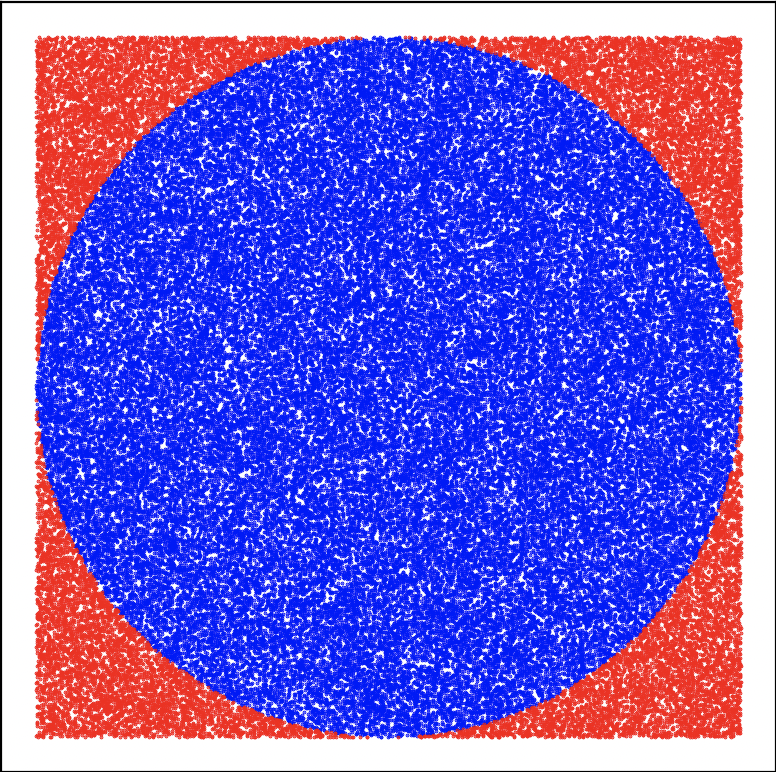

Figura 3: De izquierda a derecha: 100,000 disparos y 1 millón de disparos.


Figura 4: Aquí está la foto real de la nave espacial y el plano.
La metodología será casi la misma. Utilizamos una simulación informática donde los stormtroopers disparan aleatoriamente en la superficie del vaisseau espacial. Cada punto donde un «stormtrooper» impacta la superficie es registrado y luego se calcula el área total contando el número total de puntos y comparándolo con el tamaño total de la superficie de la nave espacial. Este método es muy eficaz ya que tiene en cuenta las formas irregulares de la superficie de la nave espacial, lo que dificultaría una estimación de área más tradicional. Sin embargo, lamentablemente, ¡esto llevaría a la destrucción total de la nave espacial!
1. Coloquen al ejército de stormtroopers en un inmenso stand de tiro cerrado.
2. Dibuja un rectángulo de 35 metros por 25 metros para representar la superficie del muro trasero y pega el Millenium Falcon encima.
3. Ordenen a los stormtroopers abrir fuego.
4. Cuenta el número de disparos que alcanzan la superficie del Millennium Falcon.
5. Utiliza la proporción de disparos que alcanzan la superficie del Millenium Falcon con respecto al número total de disparos para estimar la superficie del Millenium Falcon. Más precisamente, puedes utilizar la siguiente fórmula:
\begin{equation*}
\text{Superficie del Millennium Falcon}=35\times 25\frac{\text{Número de disparos que alcanzan el Millennium Falcon}}{\text{
Número total de disparos}}.
\end{equation*}
6. Repita estos pasos varias veces o aumente el número de stormtroopers para obtener una estimación más precisa de la superficie del Millennium Falcon.



Figura 5: De izquierda a derecha, con 10,000, 100,000 y 1 millón de disparos.
La Importancia de la Falta de Precisión
La metodología de Monte Carlo depende en gran medida de la generación de números aleatorios para simular eventos aleatorios. Aquí es donde entra en juego la falta de precisión de los stormtroopers. En el ejemplo anterior, la falta de precisión de los stormtroopers al disparar representa la aleatoriedad necesaria para que el método de Monte Carlo funcione de manera efectiva (aquí, disparan perfectamente mal). Sin esta aleatoriedad, la metodología no sería capaz de aproximar los resultados de manera precisa.
Permíteme explicarte este concepto introduciendo a Han Solo, un francotirador altamente calificado, en la simulación. La distribución de los disparos ya no sería uniformemente aleatoria, sino más bien ponderada hacia las áreas donde apunta Han Solo. Más precisamente, si estimamos su precisión de la misma manera que lo hicimos con los stormtroopers, nos damos cuenta de que dispara casi perfectamente bien.

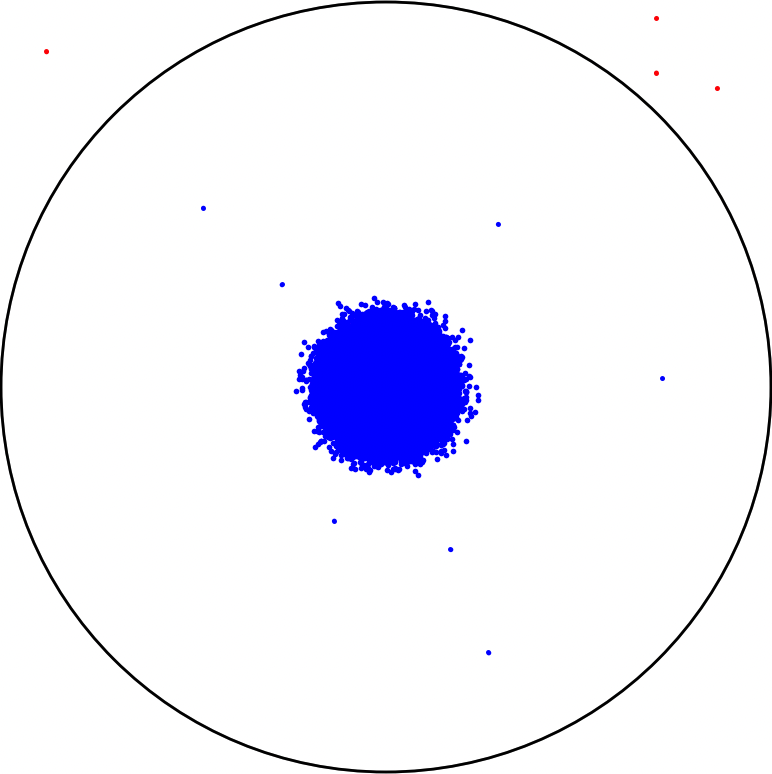
Figure 6: Han Solo disparando un millón de tiros.
Tal vez Chewbacca lo está molestando o tiene polvo en los ojos, y es por eso que su tasa de precisión no es del 100 % (eso es lo que dice). Ahora, ¿qué tan bueno es estimando π? Utilizando la misma fórmula
\begin{equation*}
\pi=\frac{\text{
El número de impactos dentro del círculo}}{\text{El número total de impactos}},
\end{equation*}
Parece que π es más o menos igual a 4 con 1 millón de tiros.
Esto destaca una consideración importante al utilizar el método de Monte Carlo: la precisión de los resultados depende en gran medida de la naturaleza aleatoria de la simulación. La introducción de sesgos o distribuciones no uniformes puede afectar considerablemente la eficacia del método. En términos simples, esto significa que para ser precisos, los números aleatorios generados deben ser verdaderamente aleatorios y no seguir un patrón predecible o ser precisos.
Generación de Números Aleatorios
Generar números aleatorios es una tarea fundamental en muchos campos, desde la informática hasta la criptografía y las simulaciones. Aunque solemos pensar que el azar es algo que ocurre naturalmente, como el lanzamiento de un dado o el volteo de una moneda, muchos números aleatorios utilizados en informática son generados mediante algoritmos sofisticados o fenómenos físicos.
Una de las técnicas ampliamente utilizadas es el generador de números pseudoaleatorios, que produce una secuencia de números que parece aleatoria, pero que en realidad se calcula de manera determinista a partir de un valor inicial llamado «semilla». Aunque no son verdaderamente aleatorios, los generadores de números pseudoaleatorios son muy eficientes y suficientemente impredecibles para satisfacer la mayoría de las necesidades prácticas. Sin embargo, pueden estar sujetos a periodicidades y correlaciones en las secuencias producidas, lo que puede plantear riesgos de seguridad en ciertas aplicaciones. Usando la analogía de Star Wars, esto sería como tener a un tirador de élite imperial perfecto que sigue un patrón de disparo; solo necesitas dar la orden para el primer disparo exitoso y cada disparo posterior será una función definida del anterior.

Figura 7: Un francotirador imperial con una parte de su patrón de disparo.
Ahora, imagina que eres un espía rebelde y deseas enviar un mensaje secreto a tu base. Para ello, necesitas un número aleatorio que sirva como clave de cifrado. Podrías utilizar un generador de números pseudo-aleatorios para crear uno, pero siempre existe el riesgo de que el Imperio haya podido predecir la secuencia de números que vas a utilizar. Para asegurarte de que tu clave de cifrado sea verdaderamente aleatoria, podrías utilizar un generador de números cuánticos.
En este ejemplo, el generador de números pseudo-aleatorios sería similar a un soldado del Imperio que sigue un plan de ataque predefinido y fácilmente predecible, al igual que el francotirador imperial. Por otro lado, el generador de números cuánticos sería similar a un científico rebelde que explota las propiedades únicas de los sables láser para encontrar soluciones impredecibles para cada situación. Como los números cuánticos se generan a partir de fenómenos cuánticos impredecibles, como la polarización, la fase o la frecuencia de los fotones, el Imperio no puede predecir la secuencia de números que vas a utilizar, lo que hace que tu mensaje secreto sea mucho más seguro. Estos generadores producen números verdaderamente aleatorios e imposibles de reproducir. Aunque todavía son relativamente nuevos y costosos, los generadores de números cuánticos ofrecen grandes perspectivas para aplicaciones que requieren los más altos niveles de seguridad e imprevisibilidad.
La Versatilidad y el Poder del Método de Monte Carlo.
En resumen, el método de Monte Carlo es una técnica matemática versátil y poderosa que permite aproximar resultados complejos que de otra manera serían difíciles de calcular con precisión. El uso de números aleatorios o pseudo-aleatorios para simular eventos aleatorios y determinar resultados probabilísticos lo convierte en una herramienta eficaz para diversas aplicaciones, como lo demostraron las simulaciones de los tiros de los stormtroopers. Las aplicaciones de este método van más allá de la estimación de constantes matemáticas y áreas de formas irregulares, incluyendo la predicción de resultados electorales, la simulación del crecimiento de la población y la estimación de la probabilidad de obtener cierto número en un juego de dados.
El método de Monte Carlo es una herramienta valiosa para numerosos campos como la física, la ingeniería y las finanzas, convirtiéndose en un componente esencial del kit de herramientas del matemático y el estadístico.

Bibliografía
M. Kalos, P. Whitlock, Monte Carlo Methods, 2008.
D. P. Kroese, T. Taimre, Z.I. Botev, Handbook of Monte Carlo Methods, 2011.
D. P. Kroese, T. Brereton, T. Taimre, Z.I. Botev, Why the Monte Carlo method is so important today, 2014.
S. Weinzierl, Introduction to Monte Carlo methods, 2000.
import random
import matplotlib.pyplot as plt
def estimate_pi(n):
num_points_circle = 0
num_points_total = 0
circle_x, circle_y = [], []
square_x, square_y = [], []
# Loop for generating random points and estimating π
for _ in range(n):
x = random.uniform(-1, 1)
y = random.uniform(-1, 1)
distance = x**2 + y**2
if distance <= 1:
num_points_circle += 1
circle_x.append(x)
circle_y.append(y)
else:
square_x.append(x)
square_y.append(y)
num_points_total += 1
# Plotting the points on a graph
plt.figure(figsize=(5, 5))
plt.scatter(circle_x, circle_y, color='blue', s=0.1)
plt.scatter(square_x, square_y, color='red', s=0.1)
plt.xlim(-1.1, 1.1)
plt.ylim(-1.1, 1.1)
plt.title("Estimation of π using the Monte Carlo method\nN = {}".format(n))
plt.show()
# Calculating and returning the estimated value of π
return 4 * num_points_circle / num_points_total
print(estimate_pi(10000))
import cv2
import numpy as np
import random
# Load the image and convert it to grayscale
img = cv2.imread("/Users/.../falcon2.png", cv2.IMREAD_GRAYSCALE)
# Apply thresholding to get a binary image
ret, thresh = cv2.threshold(img, 127, 255, cv2.THRESH_BINARY)
# Invert the colors so that black becomes white and vice versa
thresh = cv2.bitwise_not(thresh)
# Find contours in the image
contours, hierarchy = cv2.findContours(thresh, cv2.RETR_EXTERNAL, cv2.CHAIN_APPROX_SIMPLE)
# Create a black image to draw the contours
contour_img = np.zeros((img.shape[0], img.shape[1], 3), np.uint8)
# Draw the contours in white on the black image
cv2.drawContours(contour_img, contours, -1, (255, 255, 255), 2)
# Get the size of the image in pixels
height, width = img.shape[:2]
# Retrieve the size of the image in pixels
size = img.shape[:2]
# Define the real dimensions of the Millennium Falcon
real_length = 35 # in meters
real_width = 25 # in meters
# Define the resolution of the image in pixels/meter
resolution = 144
# Calculate the total number of pixels of the ship's surface
total_surface_pixels = int(real_length * real_width * resolution**2)
# Number of random points to generate for the estimation
n = 1000000
# Number of points inside the black figure
num_points_inside = 0
# Generate random points in the image and count the number of points inside the black figure
for i in range(n):
# Generate a random point in the image
x = random.randint(0, width-1)
y = random.randint(0, height-1)
# Check if the point is inside the black figure
if cv2.pointPolygonTest(contours[0], (x, y), False) == 1:
num_points_inside += 1
# Draw the point in blue
cv2.circle(contour_img, (x, y), 1, (255, 0, 0), -1)
else:
# Draw the point in red
cv2.circle(contour_img, (x, y), 1, (0, 0, 255), -1)
# Estimation of the area of the black figure using the Monte Carlo method
estimated_area = (num_points_inside / n) * (width * height)
# Display the image with points in blue and red
cv2.imshow('Image with points', contour_img)
# Wait for the user to press a key to close the window
cv2.waitKey(0)
cv2.destroyAllWindows()
# Display the estimated area of the black figure
print("Estimated area of the black figure:", estimated_area)
import random
import math
import matplotlib.pyplot as plt
num_shots = 1000000
circle_hits = 0
square_hits = 0
circle_x = []
circle_y = []
square_x = []
square_y = []
for i in range(num_shots):
x = random.gauss(0, 0.05) # shots centered at the circle's center
y = random.gauss(0, 0.05)
distance = math.sqrt(x**2 + y**2)
if distance <= 1:
circle_hits += 1
circle_x.append(x)
circle_y.append(y)
else:
square_x.append(x)
square_y.append(y)
square_hits += 1
if random.random() < 0.1: # 10% chance of shooting in the circle
if distance <= 1:
circle_hits -= 1
circle_x.pop()
circle_y.pop()
else:
circle_hits += 1
circle_x.append(x)
circle_y.append(y)
square_hits -= 1
pi_estimation = 4 * circle_hits / square_hits
print("Estimation of pi:", pi_estimation)
fig, ax = plt.subplots(figsize=(6, 6))
ax.set_xlim([-1.2, 1.2])
ax.set_ylim([-1.2, 1.2])
ax.set_aspect('equal')
ax.scatter(square_x, square_y, color='red', s=1, label='Outside the circle')
ax.scatter(circle_x, circle_y, color='blue', s=1, label='Inside the circle')
circle = plt.Circle((0, 0), 1, color='black', fill=False)
ax.add_artist(circle)
ax.legend()
plt.show()
Para encontrar el área del Millenium Falcon, utilizamos la siguiente imagen.

