Toss a Coin to Your Witcher
Par Jordan Moles le 23 Juillet, 2023

Credit: Netflix
Au cœur des terres mystérieuses de l’univers de The Witcher, où les épées se croisent et les sortilèges se déchaînent, une leçon précieuse émerge des méandres de la probabilité et du destin. Inspirée par une rencontre fortuite dans les brumes d’un bar de casino, cette leçon nous invite à plonger dans les arcanes de la loi des grands nombres, tandis que la ruine du joueur se profile telle une ombre menaçante. Préparez-vous à être transportés dans un récit envoûtant, où les dés sont lancés et les jeux de hasard jouent leur symphonie captivante.
L’Étranger et le Défi du Destin
Lors d’une soirée tumultueuse, un sorceleur solitaire nommé Geralt de Riv arpente les rues sombres d’une ville en quête de répit. Les échos de rires et de mélodies envoûtantes le guident jusqu’à un bar mystérieux, le Casino du Destin. Poussé par une curiosité irrépressible, il franchit les portes ornées et pénètre dans un monde où le sort est scellé par un simple jet de dés. Parmi la foule animée du bar, le sorceleur se retrouve attiré par un inconnu énigmatique. Le regard pétillant de malice, l’inconnu sort une pièce étincelante de sa besace. Son sourire en coin trahit une intention claire : il souhaite défier le sorceleur à un petit jeu de table. Intrigué, Geralt accepte l’invitation, se préparant à affronter le destin lui-même.
Credit: Netflix
L’inconnu, d’une voix enigmatique, expose les règles du jeu. Chacun de nous allons miser nos fortunes respectives au jeu, on supposera que Geralt et l’étranger possèdent tout deux 1000 po (pièce d’or) pour commencer. À chaque manche, le destin oscille entre les protagonistes, déterminant ainsi leur fortune sur un lancer de pièce. Chaque victoire accorde un gain de 1, tandis que chaque défaite s’accompagne d’une perte équivalente. Cette danse ensorcelante se poursuit jusqu’à ce que l’un des joueurs soit irrémédiablement ruiné, condamné à affronter les conséquences de ses choix.
Traduisons désormais cette situation en termes probabilistes, où la « destinée » est représentée par une probabilité p, , une valeur comprise entre 0 et 1; une suite de variables aléatoires indépendantes et identiquement distribuées, symbolisées par \(X_i\) ou i est la i-ème manche, , joue un rôle crucial dans le déroulement du jeu. Chaque variable \(X_i\) prend la valeur 1 avec une probabilité p, , signifiant une victoire, et la valeur -1 avec une probabilité 1-p, signifiant une défaite. En terme mathématique, cela ce note:
\begin{align*}
\mathbb{P}(X_i=1)=p,\quad \mathbb{P}(X_i=-1)=1-p.
\end{align*}
On notera aussi la fortune du sorceleur à la manche n qui est égale à la somme de sa fortune initiale et du résultat de ses gains et défaites à chaque manche par
\begin{align*}
F_n = 1000 + \sum_{i=1}^n X_i.
\end{align*}
Parallèlement, la fortune de son adversaire, intimement liée à la sienne, évolue selon des mécanismes similaires, mais avec une fortune à chaque manche de 2000-\(F_n\).
Les probabilités voilées : La quête de Geralt contre le jeu truqué
Les règles de ce jeu sont sournoises, et Geralt sent que quelque chose ne tourne pas rond. Il soupçonne le vieillard de vouloir l’arnaquer. Plongé dans une situation énigmatique, Geralt se retrouve confronté à un jeu de pièce de monnaie aux enjeux captivants. Les issues possibles sont simples : Pile ou Face, avec une probabilité égale de 50/50 si la pièce est équilibré. Cependant, il sait aussi que la pièce peut être biaisée, c’est se qui l’inquiète, avec des probabilités qui prennent des valeurs bien différentes, telles que 0, \(1/\pi\), ou 1/100ème. Le mystère s’intensifie d’autant plus que la véritable probabilité demeure inconnue.
Pour résoudre ce mystère, Geralt mobilise toutes ses compétences et ressources disponibles quitte à perdre de l’argent. Il se concentre sur les six premiers lancers de la pièce, qui donnent les résultats Pile, Face, Pile, Face, Face, Face (PFPFFF). À première vue, ces résultats semblent indiquer un déséquilibre. Cependant, Geralt entreprend une analyse approfondie des probabilités associées à chaque configuration possible. Il se souvient qu’un vieil ami Jacques Bernouilli lui avait soumis une épreuve similaire. C’était théoriquement une expérience aléatoire comportant deux issus possibles, le succès ou l’échec avec une certaine probabilité. Exactement ce a quoi il fait face aujourd’hui.
Jacques lui conta que si la pièce était équilibrée, la probabilité d’obtenir Pile en premier est de 1/2, tout comme celle d’obtenir Face en premier. En examinant les différentes combinaisons possibles (PF, PP, FF, FP), il constate que la probabilité d’obtenir Pile suivi de Face est de 1/4, tout comme pour les autres combinaisons. Cela s’explique par le fait qu’il y a quatre possibilités équiprobables avec une pièce équilibrée. Geralt se rappelle bien du raisonnement et prend conscience de l’importance des détails dans cette quête. Il réalise également que, pour trois lancers, il existe huit configurations possibles. Parmi celles-ci, il y a une chance sur huit d’obtenir Pile, Face, Pile (PFP). Geralt se rend rapidement compte de l’ampleur des calculs impliqués dans cette analyse. Plus le nombre de lancers augmente, plus la probabilité d’obtenir une configuration précise devient faible. Par exemple, la probabilité d’obtenir la configuration Pile, Face, Pile, Face, Face, Face (PFPFFF) est de \(1/2^6\), une probabilité relativement faible.
Cependant, l’objectif de Geralt ne se limite pas à déterminer des configurations spécifiques. Son véritable intérêt réside dans la proportion de Pile et de Face présente dans chaque configuration. En ces termes, le sorcelleur comprend qu’il fait fasse à une succession de n épreuves de Bernoulli indépendantes sans biais ou la variable aléatoire \(S_n\), qui compte le nombre de succès suit une loi binomiale c’est à dire que la probabilité d’avoir k « Pile » dans la somme vaut:
\begin{equation*}
\mathbb{P}(S_n=k)=\binom{n}{k}\frac{1}{2^n}.
\end{equation*}
On rappelle l’égalité suivante:
$$\binom{n}{k}=\frac{n\times(n-1)\times\cdots\times 2\times 1}{(k\times(k-1)\times\cdots\times 2\times 1)(n-k)\times(n-k-1)\times \cdots\times 2\times 1}.$$
Il pressent que si la pièce est lancée un très grand nombre de fois, la fréquence d’apparition de Pile ou de Face se révélera avec une grande précision. Son intuition s’avère juste, et les mathématiciens appellent cela la « loi des grands nombres ».
En résumé, la loi des grands nombres stipule qu’une pièce de monnaie équilibrée, lancée un nombre infini de fois, donnera Pile et Face avec une fréquence équivalente. De la même manière si la pièce est biaisée, le sorceleur verra apparaître une proportion de Pile ou de Face différente de 50/50.
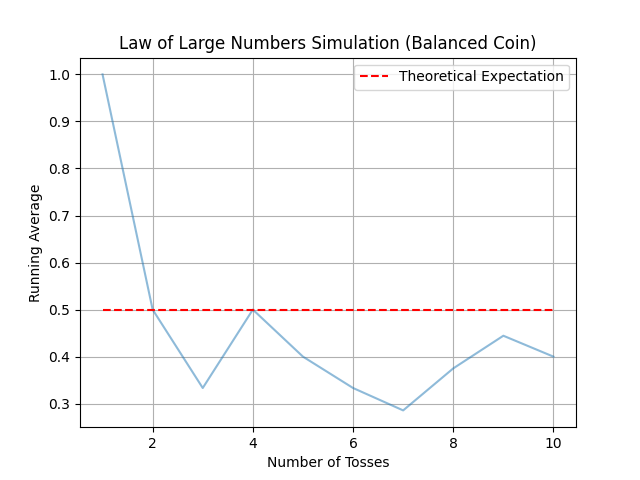
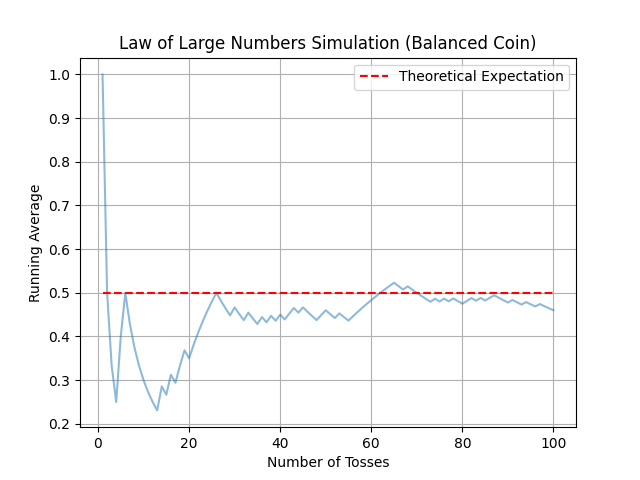
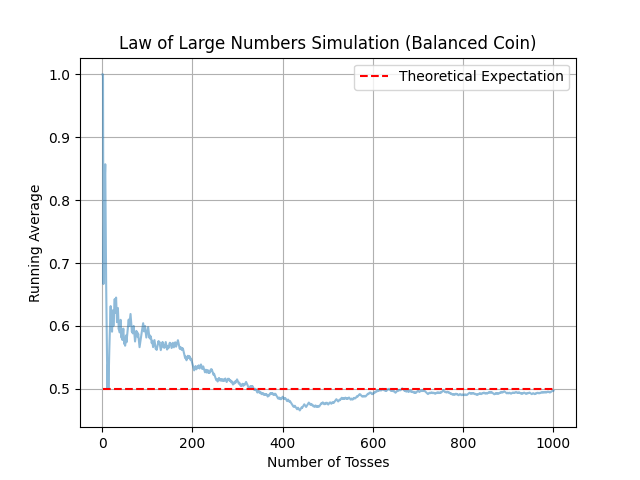



Simulation des lancers de pièce. Les graphiques illustrent comment la moyenne des faces "Pile" tend à se rapprocher de l'espérance théorique à mesure que le nombre de lancers de pièce augmente (10, 100, 1000, 10000 et 100000), même avec une pièce biaisée. Ainsi, nous pouvons clairement observer qu'à partir de 10000 lancers, la courbe bleue coïncide presque avec la moyenne théorique.
La Puissance de la Concentration : le Sorceleur Démêle le Mystère de la Pièce Biaisée
Dans le cadre du jeu proposé par l’étranger, il n’a pas la possibilité de lancer la pièce un nombre infini de fois pour vérifier la fréquence des résultats; il se rend compte qu’il doit exploiter au maximum ses capacités de concentration pour démêler le mystère de la pièce biaisée. En quête d’un avantage supplémentaire, il décide de boire une potion de concentration, qui stimule son esprit et sa clairvoyance.
Credit: Netflix
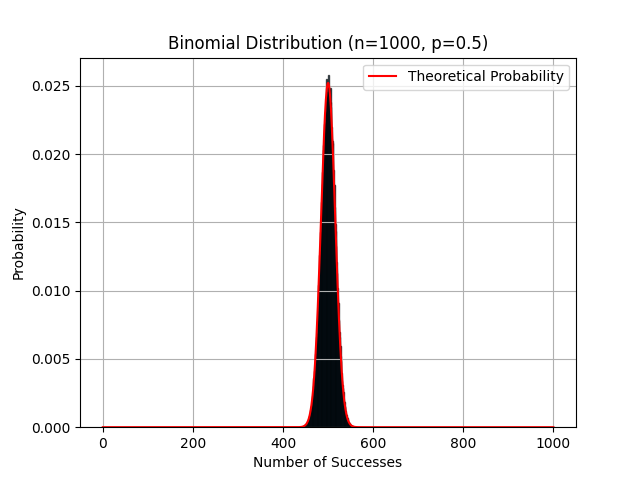

Credit: Netflix
Histogramme représentant la fréquence d'apparition des Piles sur 1000 lancers avec sa courbe théorique en cloche.
Pour mesurer expérimentalement cette fréquence d’apparition, il sait qu’il doit compter le nombre de Pile +1 dans les n lancers, le diviser par le nombre de lancer total, et estimer sa probabilité de déviation d’un certain pourcentage u par rapport à la valeur \(\frac{1}{2}\). Cela s’écrit grâce à la formule précedente, pour toutes déviations u:
\begin{equation}\label{Gauss2}
\mathbb{P}\left(\left|\frac{S_n}{n}-\frac{1}{2}\right| > u\right) \leq 2e^{-2nu^2}.
\end{equation}
Si son estimation dépasse valeur du membre de droite alors il fait face à une pièce biaisée. Ainsi Geralt, dispose d’un moyen simple de détecter un éventuel biais dans la pièce de monnaie.
Tout à coup, le temps semble se figer. Le sorceleur entre dans une transe profonde qui lui permet de lancer mentalement la pièce et d’effectuer tous les calculs nécessaires grâce à la formule précédente.

Credit: Netflix

Histogramme représentant la fréquence d'apparition des Piles sur 10 lancers avec sa courbe théorique en cloche.
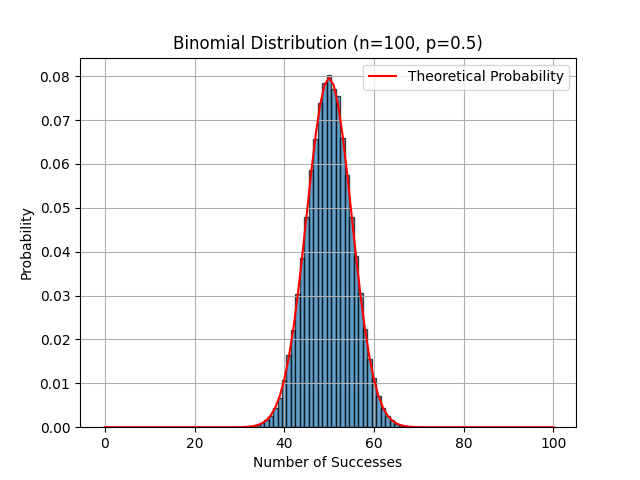
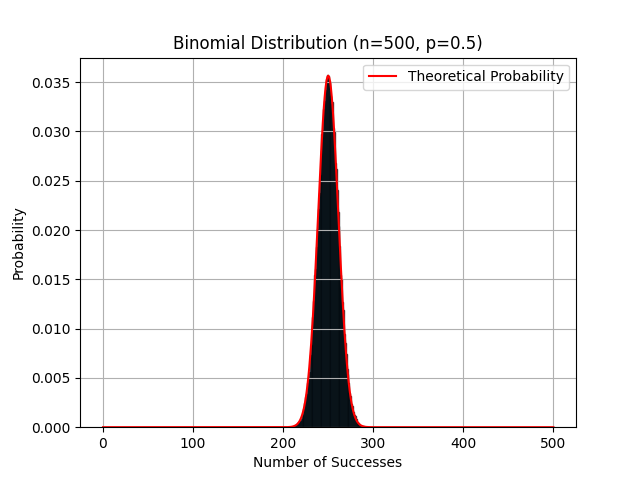
Histogramme représentant la fréquence d'apparition des Piles sur 100 et 500 lancers avec sa courbe théorique en cloche.
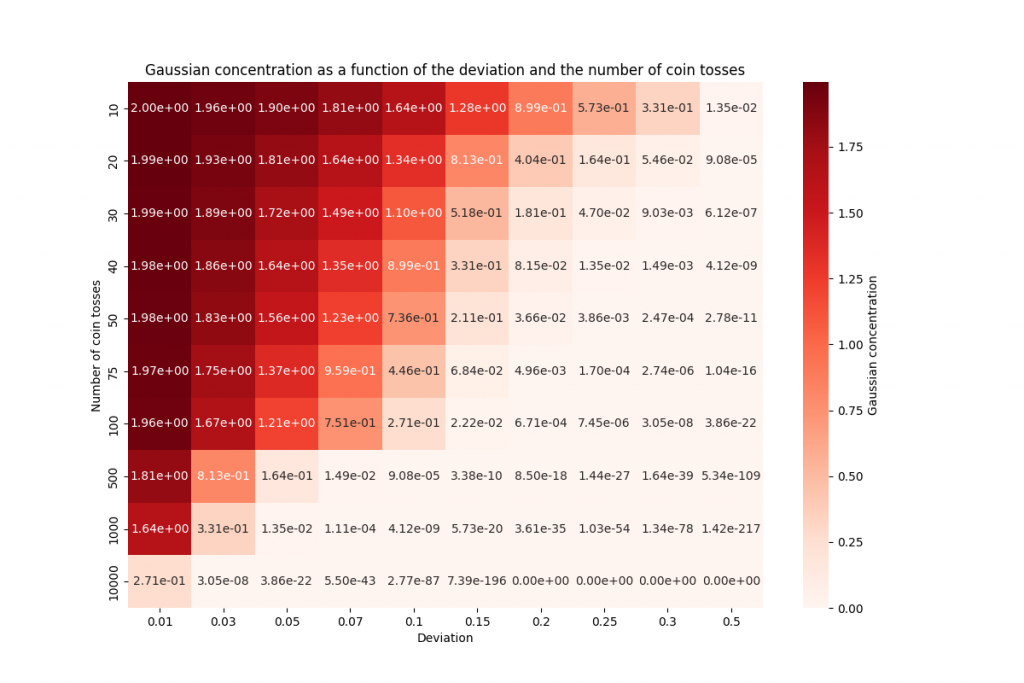
Le tableau présente les résultats obtenus par Geralt lors de ses calculs pour différentes quantités de lancers de pièce de monnaie. Les valeurs dans les cases correspondent aux probabilités estimées que la fréquence de Piles diffère de \(\frac{1}{2}\) d'un certain pourcentage (la déviation) en fonction du nombre de pièces.
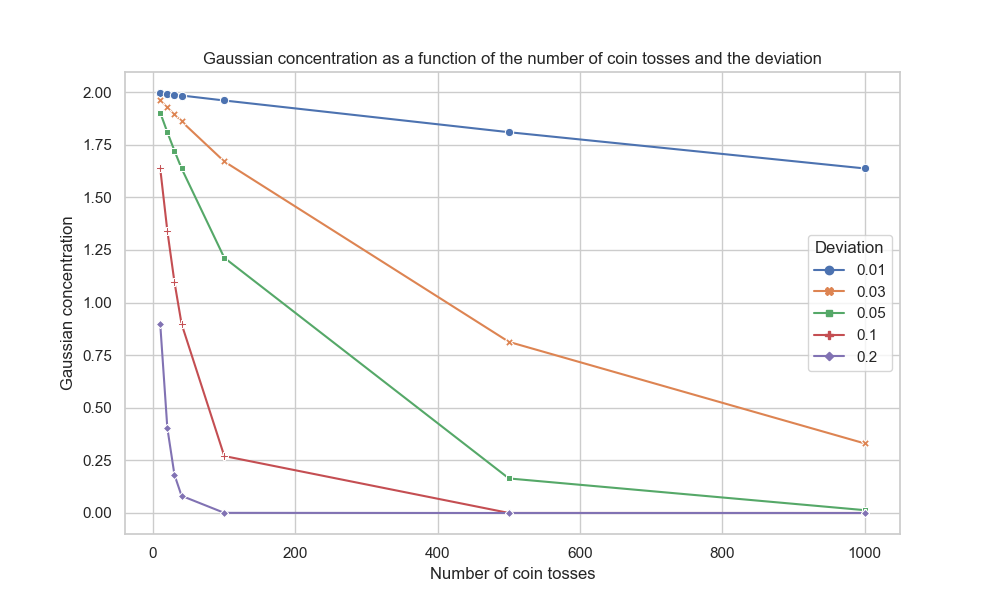
Ce graphe représente l'évolution de la concentration Gaussienne en fonction de la déviation et du nombre de pièces lancées.
En observant les données du tableau et l’évolution des courbes dans le graphe, on peut tirer les conclusions suivantes:
• Plus le nombre de lancers de pièce augmente, plus les probabilités de déviation diminuent. Cela signifie que plus Geralt lance de pièces, plus il peut estimer avec précision si la pièce est biaisée ou non.
• Pour un petit nombre de lancers (10 ou 20), les probabilités de déviation restent relativement élevées. Par exemple, pour 10 lancers, la probabilité d’une déviation de \(20\%\) est de 0.89, ce qui indique une possibilité considérable de biais. Cependant, pour 20 lancers, cette probabilité diminue à 0.40, ce qui suggère une réduction de l’incertitude.
• À mesure que le nombre de lancers augmente davantage (30, 40, 100, 500, 1000), les probabilités de déviation diminuent drastiquement. Par exemple, pour 1000 lancers, la probabilité d’une déviation de \(20\%\) est extrêmement faible, de l’ordre de \(3.6 \times 10^{-35}\), indiquant une grande confiance dans le fait que la pièce est équilibrée.
En résumé, le tableau démontre que plus Geralt effectue de lancers de pièce, plus il peut affiner son estimation de la fréquence des Piles et déterminer avec une plus grande certitude si la pièce est biaisée ou non. Les probabilités de déviation diminuent rapidement à mesure que le nombre de lancers augmente, ce qui renforce la fiabilité de la méthode de Geralt pour détecter les pièces biaisées.
Grâce à sa potion de concentration et à sa connaissance des principes probabilistes, le sorceleur, Geralt, ajuste sa stratégie de jeu et entre pleinement dans le jeu proposé par l’étranger. Il lance la pièce fournie à 500 reprises et obtient une séquence de résultats où le nombre de Piles observé est de 286, soit environ \(7\%\) de plus que le nombre attendu. Voici la séquence:
\begin{align*}
&0 0 1 0 1 0 0 0 0 1 1 1 1 1 0 1 0 1 0 0 0 1 0 11 0 1 0 1 0 0 1 0 1 1 1 1111111100011 1 1 0 0 1 1 1 1 1 1 0 1 1 0 1 0 0 1 0 1 \\
&1111 1 1 0 0 1 0 1 1 0 0 1 1 0 0 0 1 0 0 1 0 1 1 10 0 1 0 1 0 1 0 1 0 1 1 0 1 1 1 1 0 1 1 1 1 1 10 0 1 0 10 0 0 1 1 1 0 01 1 0 0 1\\
&1 1 0 0 1 0 1 1 1 1 1 0 0 1 0 1 0 1 0 1 1 1 1 11 1 1 1 0 0 1 1 1 0 0 0 1 0 1 1 0 1 1 0 0 1 1 0 0 0 1 0 1 1 1 1 10 0 0 0 11 1 1 0 0 1 0 \\
& 0 1 1 1 0 1 1 0 10 1 1 0 0 0 1 1 0 0 1 1 0 1 1 0 0 0 0 0 0 1 1 10 0 1 1 1 0 1 1 111 1 1 1 1 0 1 0 0 1 0 1 0 10 1 0 1 0 1 1 0 1 1 10 \\
& 1 1 0 0 0 1 1 1 0 1 0 00 1 1 1 1 0 1 0 0 0 0 1 1 1 0 0 1 1 1 1 0 1 0 11 0 0 1 0 1 0 1 0 1 0 0 1 0 1 0 1 1 0 1 0 0 0 01 0 1 10 1 0 0 1 \\
& 0 1 0 1 1 0 1 1 1 1 0 1 1 1 0 0 1 1 1111111 1 0 1 0 0 0 1 1 1 0 1 0 1 1 1 1 0 0 1 0 0 1 1 1 1 0 1 0 1 0 1 0 1 0 0 1 0 01 0 1 0 1 1 \\
&1 0 1 1 1 0 1 1 1 1 1 0 1 1 1 1 0 1 0 1 1 1111 0 1 1 0 0 1 1 1 0 0 1 1 1 0 1 0 1 0 0 1 0 0 0 1 1 0 1 0 1 0 0 0 1 1 0 00 0 1 1 10 1 0 \\
& 0 0 1 0 0 0 0 0 1 1 0 0 0 0 1 1 0
\end{align*}
En appliquant ces calculs, Geralt estime que la probabilité d’obtenir une telle déviation est d’environ 0,01 (ce qui est très faible). Il réalise alors qu’il est confronté à une arnaque et demande à recommencer le jeu en utilisant une autre pièce, car celle fournie est biaisée.
Il se tourne vers un croupier du casino pour obtenir une pièce officielle et équilibrée, afin de poursuivre le jeu de manière juste et équitable.

Credit: Netflix
L’Intrigue de la Ruine du Joueur: La Probabilité de Tout Perdre
Le jeu est donc équilibré, chaque joueur a donc autant de chance de gagner l’un que l’autre. Le sorceleur s’intéresse donc à la probabilité que l’inconnu soit ruiné avant lui c’est à dire que sa fortune finale \(F_{\text{Inconnu}}\) atteigne 0 avant 2000. En terme mathématique cette probabilité s’écrit:
\begin{align*}
\mathbb{P}_{Inconnu}(1000)=\mathbb{P}_{1000}\left(F\text{ atteint } 0 \text{ avant } 2000\right).
\end{align*}
Cela peut aussi se réécrire avec ce que l’on appelle des temps d’arrêts. Ce sont des temps aléatoires qui peuvent être déterminés à partir de l’information disponible sur le processus jusqu’à cet instant. Sa valeur indique le moment où une certaine condition est satisfaite ou une certaine quantité est atteinte. Le temps d’arrêt peut dépendre des réalisations passées du processus, mais il ne peut pas dépendre de l’avenir. Dans notre cas, cela peut être le temps (que l’on a appelé manche dans notre cas) que l’on note \(T_0\) ou la fortune de l’inconnu atteint 0, ou le temps \(T_{2000}\) ou elle atteint 2000. Autrement dit c’est le plus petit temps n tel que \(F_n\) soit nulle ou vaille 2000:
\begin{align*}T_0=\inf\{n\geq 0,\quad F_n =0\}\quad \text{ et } \quad T_{2000}=\inf\{n\geq 0,\quad F_n =2000\}.\end{align*}
Il est assez clair, que plus longtemps on joue plus on a de chance que le jeu s’arrête c’est à dire qu’un des deux joueurs est ruiné. Ainsi on peut écrire que la probabilité que l’étranger perde tout son or avant le sorceleur comme la probabilité que le temps d’arrêt \(T_0\) soit plus petite que \(T_{2000}\):
\begin{align*}\mathbb{P}_{Inconnu}(1000)=\mathbb{P}_{1000}\left(T_0<T_{2000}\right).\end{align*}
Aussi, il est important de noter que la fortune de l’étranger peut atteindre tous les « états » possibles (ou sa fortune peut valoir n’importe quel nombre entre 0 et 2000), nous allons noter cette valeur k. Ainsi la probabilité qu’en ayant une fortune de valeur k, il atteigne 0 avant 2000 est
\begin{align*}\mathbb{P}_{Inconnu}(k)=\mathbb{P}_{k}\left(T_0<T_{2000}\right).\end{align*}
Cette probabilité dépend seulement de la valeur de fortune à la manche précédente. En effet, comme on joue seulement une pièce d’or à chaque manche, chacun peut gagner ou perdre qu’un seul po et pas 4 d’un coup par exemple. Sans rentrer dans les détails et en gardant toutes généralités, cela signifie que la probabilité précédente vaut:
\begin{align*}
\mathbb{P}_{Inconnu}(k)=p\mathbb{P}_{Inconnu}(k+1)+(1-p)\mathbb{P}_{Inconnu}(k-1).
\end{align*}
Or la pièce est équilibrée donc cela s’écrit plutôt comme ça:
\begin{align*}
\mathbb{P}_{Inconnu}(k)=\frac{1}{2}\mathbb{P}_{Inconnu}(k+1)+\frac{1}{2}\mathbb{P}_{Inconnu}(k-1).
\end{align*}
Un oeil averti saura résoudre cette équation facilement et donnera une relation explicite de la probabilité qui nous intéresse
\begin{align*}
\mathbb{P}_{Inconnu}(k)=1-\frac{k}{2000}.
\end{align*}
Donc, si l’inconnu à une fortune de 1000, la probabilité qu’il atteigne 0 avant le sorceleur est de:
\begin{align*}
\mathbb{P}_{Inconnu}(1000)=1-\frac{1000}{2000}=\frac{1}{2}.
\end{align*}
Par une méthode analogue, on peut aussi déterminer le temps moyen d’atteinte de 0 avant 2000, noté \(\mathbb{E}_k(T)\), et vaut
\begin{align*}
\mathbb{E}_k(T)=k(2000-k).
\end{align*}
Donc, si \(k=1000\), il faudra jouer en moyenne un million de manches pour qu’un des deux atteigne \(0\). L’homme à capuche nomme donc ce concept intrigant : la ruine du joueur.
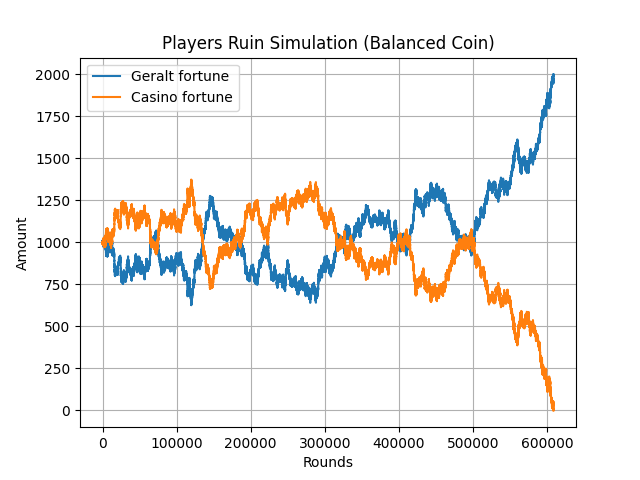
Simulation de la ruine du joueur où Geralt gagne après environ 600 000 manches.

Credit: Netflix
Le Secret du Casino : Biais, Tromperie et Probabilités Manipulées
Après une bataille acharnée, le sorceleur triomphe de son adversaire avec une grâce inégalée. Le visage masqué de l’étranger se dévoile alors, dévoilant un regard rempli d’admiration mêlée de surprise. C’est avec une voix tremblante qu’il révèle sa véritable identité, celle du puissant propriétaire du casino. Le sorceleur reste interloqué, réalisant que la fortune de cet homme dépasse de loin toutes les prédictions qui auraient pu être faites.

Credit: Netflix
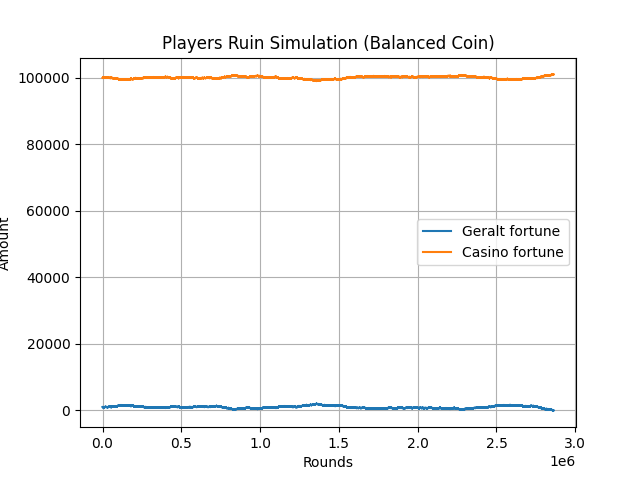

Credit: Netflix
Simulation de la ruine du joueur lorsque le casino a 100 fois plus d'argent que Geralt.
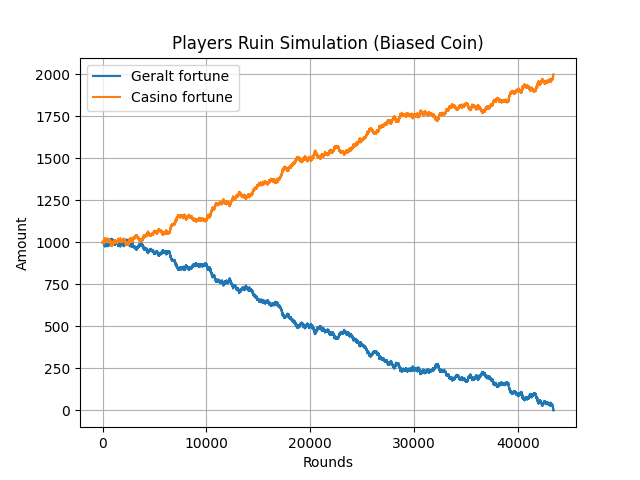

Credit: Netflix
Simulation de la ruine du joueur avec une pièce biaisée (\(p=0.49\)).
La Manipulation des Lancers de Pièce
La puissance de la potion de concentration se dissipe, et Geralt sort de sa transe. C’est à cet instant que les paroles du célèbre magicien Persi Diaconis résonnent dans l’esprit du sorceleur.
Credit: Netflix
La potion de précision qu’il détient est une création unique en son genre. Une seule gorgée de cette potion élève ses capacités à un niveau extraordinaire, lui conférant une maîtrise totale du lancer de pièce. Tel une machine, Geralt contrôle chaque aspect du lancer : les conditions initiales, le nombre de rotations effectuées dans les airs, et même le côté qui sera révélé lorsque la pièce retombera. Sa précision dans la manipulation de ces paramètres est stupéfiante, remettant en question l’idée selon laquelle le jeu du lancer de pièce serait un simple processus aléatoire.
Cette démonstration spectaculaire de maîtrise illustre parfaitement les découvertes de l’étude menée par Joe Keller dans notre réalité. En effet, cette étude révèle que le lancer de pièce, bien qu’il puisse sembler aléatoire, est en réalité régi par les lois mécaniques. Lorsqu’une pièce est lancée avec une vitesse initiale élevée et une forte rotation, elle a une probabilité d’atterrir du même côté que celui où elle a commencé, dans près de la moitié des cas. Cependant, si l’on prend en compte la précession, c’est-à-dire le changement de l’axe de rotation de la pièce pendant son vol, le résultat peut différer. Si l’angle entre le moment angulaire et la normale de la pièce est inférieur à 45 degrés, la pièce ne se retournera jamais et retombera toujours du même côté.
Grâce à sa potion de précision, Geralt met en lumière la possibilité de manipuler les lancers de pièce de manière contrôlée, créant ainsi l’illusion d’un jeu aléatoire tout en étant conscient que les résultats sont en réalité déterminés par des facteurs mécaniques. au cœur de cette manipulation se trouve un élément crucial : la main qui lance la pièce ne la tient pas toujours du même côté, jonglant entre face et pile. C’est bien la randomisation inconsciente effectuée par la personne lançant la pièce, lorsqu’elle la place sur son pouce avant de lui donner une légère impulsion initiale, qui uniformise les probabilités d’obtenir face ou pile. Ainsi, le résultat du lancer tend vers l’égalité.

Credit: Netflix
Toutefois, pour ceux qui aspirent à une légère avance, un entraînement assidu au lancer de précision peut leur permettre de maîtriser cet art subtil et d’amener la pièce à atterrir selon leurs désirs. Mais dans leur ingéniosité, les jeux de hasard introduisent une autre composante aléatoire : un autre joueur doit crier « Pile » ou « Face » au moment précis où la pièce virevolte dans les airs, échappant ainsi à toute prédiction.
Dans cette romance envoûtante, nous pouvons ainsi apprécier l’importance de cet équilibre entre précision et aléatoire. Geralt de Riv, malgré sa maîtrise extraordinaire du lancer de pièce grâce à sa potion de précision, réalise que la véritable essence du jeu réside dans cette randomisation inconsciente, qui assure une équité des probabilités. Le lancer de pièce demeure un jeu fascinant où l’incertitude et la magie de l’instant se mêlent harmonieusement, éveillant en chacun une curiosité teintée de mystère.
Révélations du Lancer de Pièce : L’Intuition de Geralt
Dans les sombres méandres des jeux de hasard, où le sort des âmes joueuses se décide en un simple lancer de pièce, Geralt de Riv, le légendaire sorceleur, a dévoilé une vérité troublante. Il met en évidence l’importance des probabilités et des outils statistiques pour comprendre et analyser les situations aléatoires. Malgré les apparences, Geralt se rend compte que le jeu de la pièce de monnaie est en réalité un jeu de probabilités et de chances. Grâce à son intelligence et à sa potion de concentration, il utilise des concepts tels que la loi des grands nombres et l’inégalité de concentration Gaussienne pour évaluer les probabilités et les risques associés aux lancers de pièce.
Bien qu’il ne puisse pas lancer la pièce un nombre infini de fois, il parvient à obtenir des estimations fiables de la proportion de Pile et de Face en utilisant des résultats probabilistes et statistiques. La quête de Geralt souligne également l’importance de la prudence et de la connaissance de soi dans les jeux de hasard. En étant conscient des probabilités et des risques, Geralt prend des décisions éclairées et minimise les conséquences de ses choix.
Ainsi, que vous soyez un aventurier solitaire aux confins du monde réel ou un joueur intrépide dans les arcanes des casinos, souvenez-vous toujours que derrière le voile de l’illusion se cache la vérité mathématique implacable. Et comme Geralt l’a compris, parfois, la plus grande victoire réside dans la sagesse de savoir quand s’éloigner de la table de jeu, laissant derrière soi les mirages éphémères pour embrasser une réalité plus stable. Celle de son bain.

Credit: Netflix
Bibliographie
D. Chafaï, F. Malrieu, Recueil de modèles aléatoires, 2015.
T. Bodineaux, Modélisation de phénomènes aléatoires : introduction aux chaînes de Markov et aux martingales, 2015
M. Ledoux, The concentration of measure phenomenon, 2001
I, Stewart, Do dice play god?, 2019
R. Epstein, The Theory of Gambling and Statistical Logic (Revised ed.), 1995
J. L. Coolidge, The Gambler’s Ruin. Annals of Mathematics. 10 (4): 181–192, 1909
import numpy as np
import matplotlib.pyplot as plt
def simulate_biased_coin_tosses(n, p, num_trials):
"""
Simulates multiple trials of biased coin tosses and plots the running average.
Args:
n (int): Number of coin tosses in each trial.
p (float): Probability of getting heads (biased coin).
num_trials (int): Number of trials to simulate.
"""
results = []
for _ in range(num_trials):
coin_tosses = np.random.choice([0, 1], size=n, p=[1-p, p])
running_average = np.cumsum(coin_tosses) / np.arange(1, n + 1)
results.append(running_average)
# Plot the results
for i, running_average in enumerate(results):
plt.plot(np.arange(1, n + 1), running_average, alpha=0.5)
# Plot the theoretical expectation (p for a biased coin)
plt.plot(np.arange(1, n + 1), np.full(n, p), color='red', linestyle='--', label='Theoretical Expectation')
plt.xlabel('Number of Tosses')
plt.ylabel('Running Average')
plt.title('Law of Large Numbers Simulation (Balanced Coin)')
plt.legend()
plt.grid()
plt.show()
# Parameters
n = 100000 # Number of coin tosses in each trial
p = 0.5 # Probability of getting heads (biased coin)
num_trials = 1 # Number of trials to simulate
# Perform the simulation and visualize the results
simulate_biased_coin_tosses(n, p, num_trials)
import numpy as np
import matplotlib.pyplot as plt
def simulate_binomial_distribution(n, p, num_trials):
"""
Simulates multiple trials of a binomial distribution and plots the histogram of outcomes.
Args:
n (int): Number of trials in each binomial experiment.
p (float): Probability of success in each trial.
num_trials (int): Number of trials to simulate.
"""
results = np.random.binomial(n, p, size=num_trials)
# Plot the histogram of outcomes
plt.hist(results, bins=np.arange(n + 1) - 0.5, density=True, alpha=0.7, edgecolor='black')
# Plot the theoretical probability mass function
x = np.arange(n + 1)
y = np.array([np.math.comb(n, k) * p**k * (1 - p)**(n - k) for k in x])
plt.plot(x, y, color='red', label='Theoretical Probability')
plt.xlabel('Number of Successes')
plt.ylabel('Probability')
plt.title(f'Binomial Distribution (n={n}, p={p})')
plt.legend()
plt.grid()
plt.show()
# Parameters
n =10 # Number of trials in each binomial experiment
p = 0.5 # Probability of success in each trial
num_trials = 100000 # Number of trials to simulate
# Perform the simulation and visualize the results
simulate_binomial_distribution(n, p, num_trials)
# Importing libraries
import numpy as np
import pandas as pd
import seaborn as sns
from scipy.stats import norm
import matplotlib.pyplot as plt
# Function to simulate coin toss
def coin_toss(n, deviation):
coin = np.random.choice([0, 1], size=n) # Simulating coin toss
proportion = np.mean(coin) # Calculating proportion of Heads
concentration = 2 * np.exp(-2 * n * deviation**2) # Calculating Gaussian concentration
return proportion, concentration
# Parameters for simulation
n_values = [10, 20, 30, 40, 50, 75, 100, 500, 1000, 10000]
deviation_values = [0.01, 0.03, 0.05, 0.07, 0.1, 0.15, 0.2, 0.25, 0.3, 0.5]
# Simulation and calculation of Gaussian concentration for each combination of parameters
results = []
for n in n_values:
row = []
for deviation in deviation_values:
proportion, concentration = coin_toss(n, deviation)
row.append(concentration)
results.append(row)
# Creating DataFrame from results
df = pd.DataFrame(results, columns=deviation_values, index=n_values)
# Displaying results as a table
print("Number of coin tosses\t", end="")
for deviation in deviation_values:
print(f"Deviation {deviation}\t", end="")
print()
for i, n in enumerate(n_values):
row_str = f"{n}\t\t"
for j, deviation in enumerate(deviation_values):
row_str += f"{results[i][j]:.3e}\t"
print(row_str)
# Creating heatmap with Seaborn
plt.figure(figsize=(12, 8))
sns.heatmap(data=df, annot=True, cmap="Reds", fmt=".2e", cbar=True, cbar_kws={'label': 'Gaussian concentration'})
plt.xlabel("Deviation")
plt.ylabel("Number of coin tosses")
plt.title("Gaussian concentration as a function of the deviation and the number of coin tosses")
plt.show()
# Importing libraries
import numpy as np
import pandas as pd
import seaborn as sns
from scipy.stats import norm
import matplotlib.pyplot as plt
# Function to simulate coin toss
def coin_toss(n, deviation):
coin = np.random.choice([0, 1], size=n) # Simulating coin toss
proportion = np.mean(coin) # Calculating proportion of Heads
concentration = 2 * np.exp(-2 * n * deviation**2) # Calculating Gaussian concentration
return proportion, concentration
# Parameters for simulation
n_values = [10, 20, 30, 40, 100, 500, 1000]
deviation_values = [0.01, 0.03, 0.05, 0.1, 0.2]
# Simulation and calculation of Gaussian concentration for each combination of parameters
results = []
for n in n_values:
row = []
for deviation in deviation_values:
proportion, concentration = coin_toss(n, deviation)
row.append(concentration)
results.append(row)
# Creating DataFrame from results
df = pd.DataFrame(results, columns=deviation_values, index=n_values)
# Displaying results as a table
print("Number of coin tosses\tDeviation 0.01\tDeviation 0.03\tDeviation 0.05\tDeviation 0.1\tDeviation 0.2")
for i, n in enumerate(n_values):
row_str = f"{n}\t\t"
for j, deviation in enumerate(deviation_values):
row_str += f"{results[i][j]:.3e}\t"
print(row_str)
# Creating the graph with Seaborn
sns.set(style="whitegrid")
plt.figure(figsize=(10, 6))
sns.lineplot(data=df, markers=True, dashes=False)
plt.xlabel("Number of coin tosses")
plt.ylabel("Gaussian concentration")
plt.title("Gaussian concentration as a function of the number of coin tosses and the deviation")
plt.legend(title="Deviation")
plt.show()
import numpy as np
import matplotlib.pyplot as plt
def simulate_ruin(player_a_amount, player_b_amount, win_probability):
"""
Simulates the ruin of two players in a gambling game and returns the number of rounds played.
Args:
player_a_amount (int): Initial amount of money for player A.
player_b_amount (int): Initial amount of money for player B.
win_probability (float): Probability of winning a bet.
Returns:
int: Number of rounds played until one of the players goes broke.
"""
rounds = 0
while player_a_amount > 0 and player_b_amount > 0:
# Simulate a round of the game
if np.random.rand() < win_probability:
player_a_amount += 1 # Player A wins
player_b_amount -= 1 # Player B loses
else:
player_a_amount -= 1 # Player A loses
player_b_amount += 1 # Player B wins
rounds += 1
return rounds
def simulate_ruin_visual(player_a_amount, player_b_amount, win_probability):
"""
Simulates the ruin of two players in a gambling game with a biased coin and visualizes the results.
Args:
player_a_amount (int): Initial amount of money for player A.
player_b_amount (int): Initial amount of money for player B.
win_probability (float): Probability of winning a bet.
"""
player_a_history = [player_a_amount]
player_b_history = [player_b_amount]
rounds = 0
while player_a_amount > 0 and player_b_amount > 0:
# Simulate a round of the game with a biased coin
if np.random.rand() < win_probability:
player_a_amount += 1 # Player A wins
player_b_amount -= 1 # Player B loses
else:
player_a_amount -= 1 # Player A loses
player_b_amount += 1 # Player B wins
rounds += 1
player_a_history.append(player_a_amount)
player_b_history.append(player_b_amount)
# Plot the results
plt.plot(player_a_history, label='Geralt fortune')
plt.plot(player_b_history, label='Casino fortune')
plt.xlabel('Rounds')
plt.ylabel('Amount')
plt.title('Players Ruin Simulation (Balanced Coin)')
plt.legend()
plt.grid()
plt.show()
# Parameters
player_a_amount = 1000 # Initial amount of money for player A
player_b_amount = 1000 # Initial amount of money for player B
win_probability = 0.5 # Probability of winning a bet (balanced coin)
# Perform the simulation and get the number of rounds played
rounds_played = simulate_ruin(player_a_amount, player_b_amount, win_probability)
print("Number of rounds played:", rounds_played)
# Perform the simulation and visualize the results
simulate_ruin_visual(player_a_amount, player_b_amount, win_probability)

