Toss a Coin to Your Witcher
Por Jordan Moles el 23 de Julio, 2023

Credit: Netflix
En el corazón de las misteriosas tierras del universo de The Witcher, donde las espadas chocan y los hechizos se desatan, emerge una valiosa lección de los meandros de la probabilidad y el destino. Inspirada por un encuentro fortuito en las brumas de un bar de casino, esta lección nos invita a sumergirnos en los secretos de la ley de los grandes números, mientras la ruina del jugador se cierne como una sombra amenazante. Prepárate para ser transportado a un relato encantador, donde los dados son lanzados y los juegos de azar interpretan su cautivadora sinfonía.
El Extranjero y el Desafío del Destino
Durante una noche tumultuosa, un solitario brujo llamado Geralt de Rivia camina por las oscuras calles de una ciudad en busca de descanso. Los ecos de risas y melodías hipnóticas lo guían hasta un misterioso bar, el Casino del Destino. Impulsado por una curiosidad irresistible, atraviesa las ornamentadas puertas y entra en un mundo donde el destino se sella con un simple lanzamiento de dados. Entre la animada multitud del bar, el brujo se siente atraído por un enigmático desconocido. Con una mirada chispeante de malicia, el desconocido saca una moneda brillante de su bolsa. Su sonrisa insinuante traiciona una clara intención: desafiar al brujo a un pequeño juego de mesa. Intrigado, Geralt acepta la invitación, preparándose para enfrentar al propio destino.
Credit: Netflix
El desconocido, con una voz enigmática, explica las reglas del juego. Cada uno de nosotros apostará nuestras respectivas fortunas en el juego, suponiendo que Geralt y el desconocido tienen ambos 1000 monedas de oro para comenzar. En cada ronda, el destino oscila entre los protagonistas, determinando así su fortuna en un lanzamiento de moneda. Cada victoria otorga una ganancia de 1, mientras que cada derrota conlleva una pérdida equivalente. Esta danza encantadora continúa hasta que uno de los jugadores quede irremediablemente arruinado, condenado a enfrentar las consecuencias de sus elecciones.
Ahora traduzcamos esta situación a términos probabilísticos, donde el «destino» está representado por una probabilidad p, un valor comprendido entre 0 y 1; Una secuencia de variables aleatorias independientes e idénticamente distribuidas, simbolizadas por \(X_i\) donde i es la i-ésima ronda, juega un papel crucial en el desarrollo del juego. Cada variable \(X_i\) toma el valor 1 con probabilidad p, lo que significa una victoria, y toma el valor -1 con probabilidad 1-p, lo que significa una derrota. Matemáticamente, esto se expresa como:
\begin{align*}
\mathbb{P}(X_i=1)=p,\quad \mathbb{P}(X_i=-1)=1-p.
\end{align*}
Se debe también tener en cuenta la fortuna del sorceleur en la ronda \(n\), que es igual a la suma de su fortuna inicial y el resultado de sus ganancias y derrotas en cada ronda, representado por:
\begin{align*}
F_n = 1000 + \sum_{i=1}^n X_i.
\end{align*}
Paralelamente, la fortuna de su adversario, estrechamente vinculada a la suya, evoluciona según mecanismos similares, pero con una fortuna en cada ronda de 2000-\(F_n\).
Las Probabilidades Veladas: La Búsqueda de Geralt Contra el Juego Amañado
Las reglas de este juego son astutas, y Geralt siente que algo no está bien. Sospecha que el viejo pretende engañarlo. Sumergido en una situación enigmática, Geralt se enfrenta a un juego de lanzamiento de monedas con apuestas cautivadoras. Las posibles opciones son simples: Águila o Sol con una probabilidad igual de 50/50 si la moneda es equilibrada. Sin embargo, también sabe que la moneda puede estar sesgada, lo cual le preocupa, con probabilidades que toman valores diferentes, como 0, \(1/\pi\), o 1/100. El misterio se intensifica aún más ya que la verdadera probabilidad permanece desconocida.
Para resolver este misterio, Geralt moviliza todas sus habilidades y recursos disponibles, incluso si eso significa perder dinero. Se concentra en los seis primeros lanzamientos de la moneda, que dan los resultados Águila, Sol, Águila, Sol, Sol, Sol (ÁSÁSS). A primera vista, estos resultados parecen indicar un desequilibrio. Sin embargo, Geralt emprende un análisis detallado de las probabilidades asociadas con cada configuración posible. Recuerda que un viejo amigo, Jacques Bernouilli, le había presentado una prueba similar en el pasado. Teóricamente, era un experimento aleatorio con dos posibles resultados, éxito o fracaso, con una cierta probabilidad. Exactamente lo que enfrenta hoy.
Jacques le explicó que si la moneda estaba equilibrada, la probabilidad de obtener Águila primero era de 1/2, al igual que la probabilidad de obtener Sol primero. Al examinar las diferentes combinaciones posibles (ÁS, ÁÁ, SS, SA), Geralt observó que la probabilidad de obtener Águila seguido de Sol era de 1/4, al igual que para las demás combinaciones. Esto se debe a que hay cuatro posibilidades equiprobables con una moneda equilibrada. Geralt recordó bien el razonamiento y se dio cuenta de la importancia de los detalles en esta búsqueda. También se dio cuenta de que, para tres lanzamientos, hay ocho configuraciones posibles. Entre ellas, hay una posibilidad entre ocho de obtener Águila, Sol, Águila (ÁSÁ). Geralt rápidamente se dio cuenta de la magnitud de los cálculos involucrados en este análisis. A medida que aumenta el número de lanzamientos, la probabilidad de obtener una configuración específica se vuelve más baja. Por ejemplo, la probabilidad de obtener la configuración Águila, Sol, Águila, Sol, Sol, Sol (ÁSÁSS) es de \(1/2^6\), una probabilidad relativamente baja.
Sin embargo, el objetivo de Geralt no se limita a determinar configuraciones específicas. Su verdadero interés radica en la proporción de Águila y Sol presente en cada configuración. En estos términos, el brujo comprende que se enfrenta a una sucesión de n pruebas de Bernoulli independientes y sin sesgo, donde la variable aleatoria \(S_n\), que cuenta el número de éxitos sigue una distribución binomial, lo que significa que la probabilidad de obtener k «Águila» en la suma es
\begin{equation*}
\mathbb{P}(S_n=k)=\binom{n}{k}\frac{1}{2^n}.
\end{equation*}
Recordemos la siguiente igualdad:
$$\binom{n}{k}=\frac{n\times(n-1)\times\cdots\times 2\times 1}{(k\times(k-1)\times\cdots\times 2\times 1)(n-k)\times(n-k-1)\times \cdots\times 2\times 1}.$$
Siente que si la moneda es lanzada un gran número de veces, la frecuencia de aparición de Aguila o Sol se revelará con gran precisión. Su intuición resulta correcta, y los matemáticos lo llaman la «ley de los grandes números».
En resumen, la ley de los grandes números establece que una moneda equilibrada, lanzada un número infinito de veces, mostrará Aguila y Sol con una frecuencia equivalente. De manera similar, si la moneda está sesgada, el hechicero verá una proporción de Aguila o Sol diferente de 50/50.
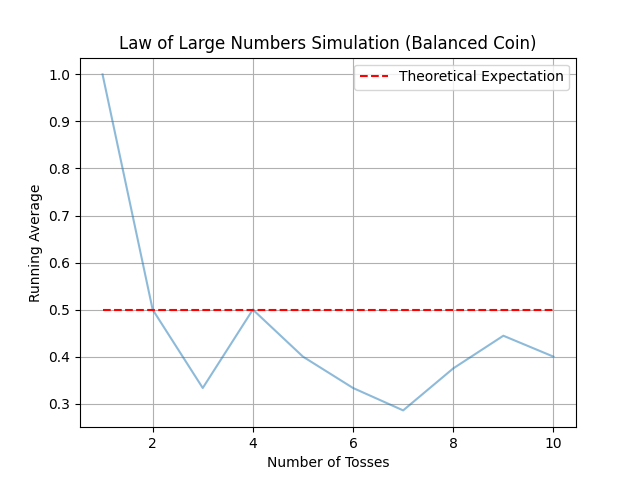
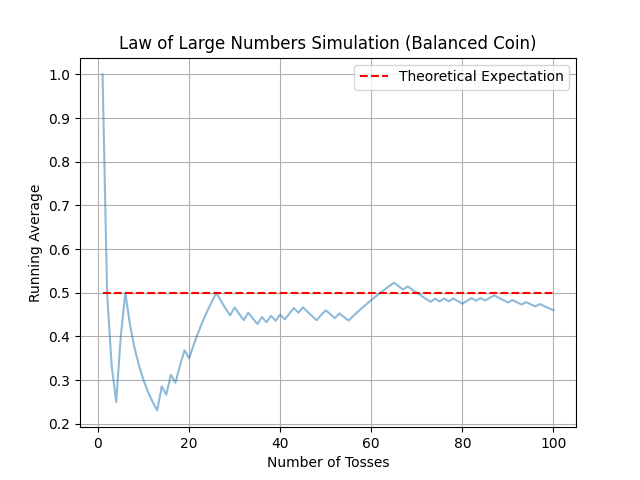
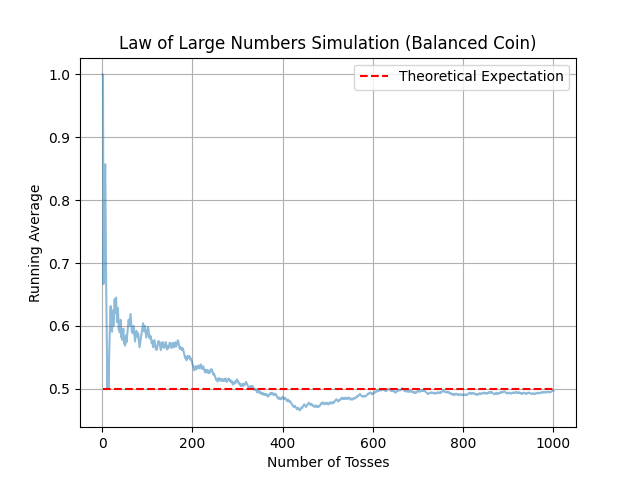



Simulación de lanzamientos de moneda. Los gráficos ilustran cómo el promedio de caras "Aguila" tiende a acercarse a la esperanza teórica a medida que aumenta el número de lanzamientos de moneda (10, 100, 1000, 10000 y 100000), incluso con una moneda sesgada. Por lo tanto, podemos observar claramente que a partir de 10000 lanzamientos, la curva azul casi coincide con la media teórica.
El Poder de la Concentración: el Brujo Desentraña el Misterio de la Moneda Sesgada
En el marco del juego propuesto por el desconocido, no tiene la posibilidad de lanzar la moneda un número infinito de veces para verificar la frecuencia de los resultados; se da cuenta de que debe aprovechar al máximo sus habilidades de concentración para desentrañar el misterio de la moneda sesgada. En busca de una ventaja adicional, decide beber una poción de concentración, que estimula su mente y clarividencia.
Credit: Netflix
Guiado por el efecto de la poción, Geralt se sumerge en un análisis profundo del lanzamiento de la moneda. Utiliza la notación binaria donde «Aguila» se representa con 1 y «Sol» con 0. Por lo tanto, \(S_n\) representa el número de «Aguilas» en una secuencia. En el caso de que Geralt crea que la moneda es equilibrada, la probabilidad de obtener «Aguila» (o +1) en el i-ésimo lanzamiento es de 1/2, lo mismo ocurre con «Sol» (o 0) y esto se expresa como:
\begin{equation*}
\mathbb{P}(X_i=+1)=\mathbb{P}(X_i=0)=\frac{1}{2}.
\end{equation*}
Entonces, \(\mathbb{E}(S_n) = \frac{n}{2}\) porque hay tantos +1 como 0 en los resultados, el valor promedio teórico debe ser \(\frac{n}{2}\).
Se da cuenta de que para obtener una estimación confiable de la proporción de Águila y Sol con un número limitado de lanzamientos, debe recurrir a herramientas estadísticas desarrolladas como la desigualdad de concentración gaussiana. Esta desigualdad, también conocida como desigualdad de Hoeffding, es un resultado fundamental en probabilidad y estadísticas que funciona bien en este caso específico. Proporciona una estimación de la probabilidad de que una variable aleatoria, en este caso los resultados del lanzamiento de la moneda, se aleje significativamente de su media. Proporciona límites sobre la probabilidad de observar eventos raros o extremos. En lenguaje matemático, esto se expresa como, para todas las desviaciones u:
\begin{equation}\label{Gauss}
\mathbb{P}\left(\left|S_n-\mathbb{E}(S_n)\right|\geq u\right)\leq 2e^{-\frac{2u^2}{n}}
\end{equation}
donde \(S_n = X_1 + \cdots + X_n\) es el resultado de n lanzamientos de moneda y \(\mathbb{E}(S_n)\) es su esperanza (en cierto modo su promedio teórico). El uso del término ‘concentración gaussiana’ en el contexto de esta desigualdad hace referencia a la capacidad de las variables aleatorias para agruparse alrededor de su media, siguiendo una distribución cercana a la distribución normal o gaussiana, también conocida como curva de campana. Indica que la probabilidad de observaciones lejanas a la media disminuye rápidamente (muy, muy rápidamente) a medida que aumenta la desviación estándar.
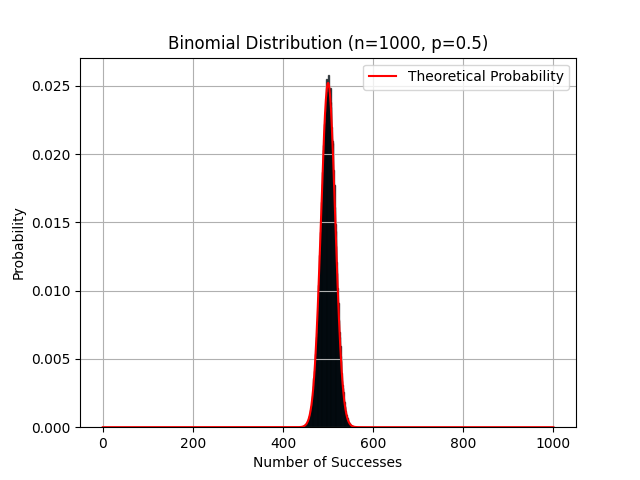

Credit: Netflix
Histograma que muestra la frecuencia de aparición de Caras en 1000 lanzamientos con su curva teórica en forma de campana.

Credit: Netflix
Su primer cálculo consiste en estimar la probabilidad de que, en 10 lanzamientos de una moneda equilibrada, el porcentaje de «Aguila» sea superior o inferior de \(20\%\) en comparación con el número de Sol. Él encuentra:
\begin{equation*}
\mathbb{P}\left(\left|\frac{S_{10}}{10}-\frac{1}{2}\right|>0.2\right)\leq 2e^{- 20\times 0.04}\approx 0.89.
\end{equation*}
En la siguiente figura, esto significa que la suma del área bajo la curva roja entre 7 y 10, y entre 0 y 3, es menor que 0.89.

Histograma que muestra la frecuencia de aparición de Aguilas en 10 lanzamientos con su correspondiente curva teórica en forma de campana.
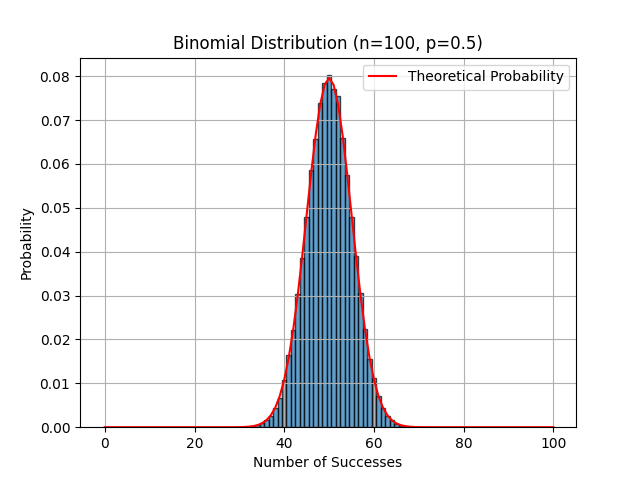
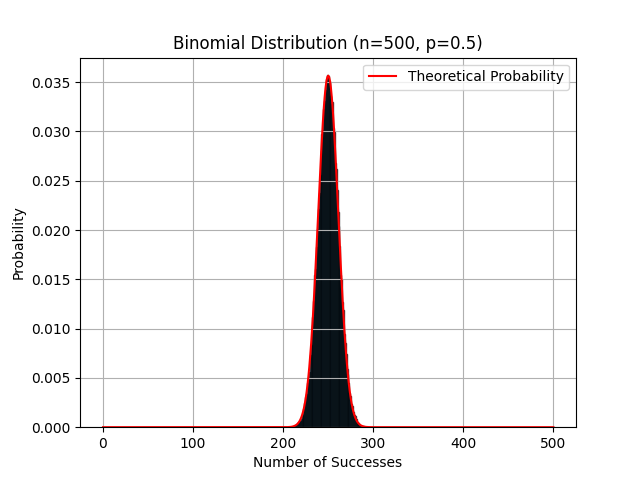
Histograma que muestra la frecuencia de aparición de Aguila en 100 y 500 lanzamientos, junto con su curva teórica en forma de campana.
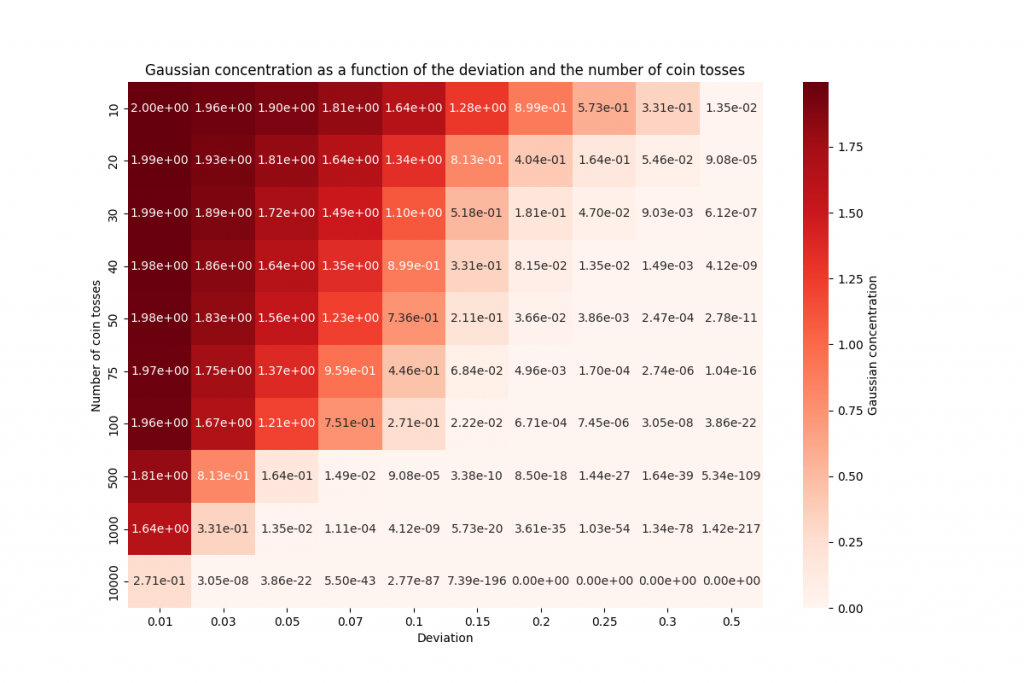
El cuadro presenta los resultados obtenidos por Geralt en sus cálculos para diferentes cantidades de lanzamientos de la moneda. Los valores en las casillas corresponden a las probabilidades estimadas de que la frecuencia de Caras difiera de \(\frac{1}{2}\) en cierto porcentaje (la desviación) en función del número de lanzamientos.
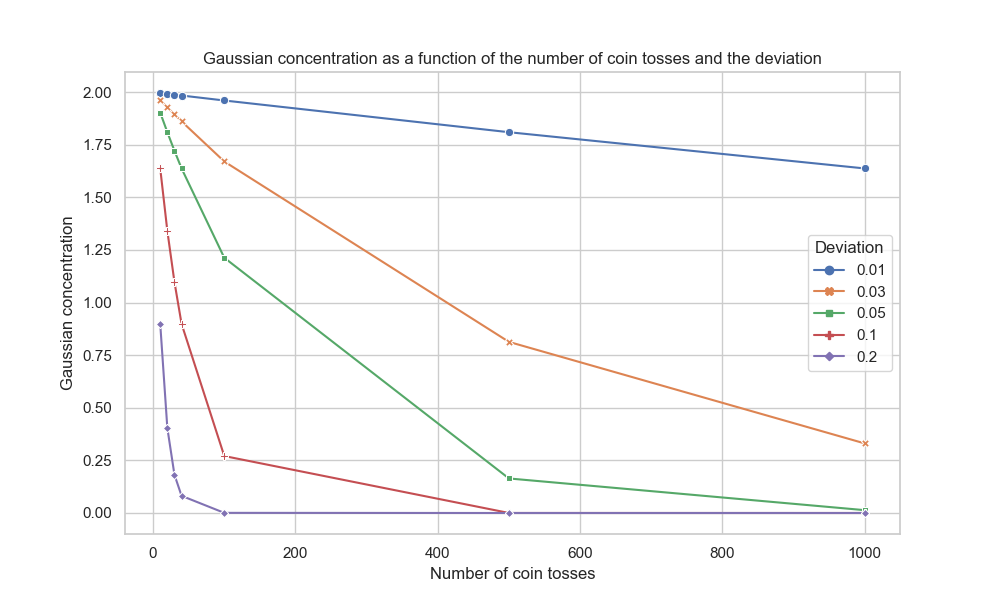
Este gráfico representa la evolución de la concentración gaussiana en función de la desviación y del número de lanzamientos de monedas.
Al observar los datos de la tabla y la evolución de las curvas en el gráfico, podemos llegar a las siguientes conclusiones:
• Cuanto mayor sea el número de lanzamientos de monedas, menor será la probabilidad de desviación. Esto significa que cuanto más lance Geralt la moneda, más precisamente puede estimar si la moneda está sesgada o no.
• Para un pequeño número de lanzamientos (10 o 20), las probabilidades de desviación siguen siendo relativamente altas. Por ejemplo, para 10 lanzamientos, la probabilidad de una desviación de \(20\%\) es de 0.89, lo que indica una posibilidad considerable de sesgo. Sin embargo, para 20 lanzamientos, esta probabilidad disminuye a 0.40, lo que sugiere una reducción de la incertidumbre.
• A medida que el número de lanzamientos aumenta aún más (30, 40, 100, 500, 1000), las probabilidades de desviación disminuyen drásticamente. Por ejemplo, para 1000 lanzamientos, la probabilidad de una desviación de \(20\%\) es extremadamente bajo, del orden de \(3.6 \times 10^{-35}\), indicando una gran confianza en que la moneda está equilibrada.
En resumen, la tabla demuestra que a medida que Geralt realiza más lanzamientos de monedas, puede afinar su estimación de la frecuencia de «Águilas» y determinar con mayor certeza si la moneda está sesgada o no. Las probabilidades de desviación disminuyen rápidamente a medida que aumenta el número de lanzamientos, lo que refuerza la confiabilidad del método de Geralt para detectar monedas sesgadas.
Gracias a su poción de concentración y su conocimiento de los principios probabilísticos, el brujo Geralt ajusta su estrategia de juego y se sumerge por completo en el juego propuesto por el desconocido. Lanza la moneda proporcionada 500 veces y obtiene una secuencia de resultados donde el número de Águilas observadas es de 286, aproximadamente \(7\%\) más que el número esperado. Aquí está la secuencia:
\begin{align*}
&0 0 1 0 1 0 0 0 0 1 1 1 1 1 0 1 0 1 0 0 0 1 0 11 0 1 0 1 0 0 1 0 1 1 1 1111111100011 1 1 0 0 1 1 1 1 1 1 0 1 1 0 1 0 0 1 0 1 \\
&1111 1 1 0 0 1 0 1 1 0 0 1 1 0 0 0 1 0 0 1 0 1 1 10 0 1 0 1 0 1 0 1 0 1 1 0 1 1 1 1 0 1 1 1 1 1 10 0 1 0 10 0 0 1 1 1 0 01 1 0 0 1\\
&1 1 0 0 1 0 1 1 1 1 1 0 0 1 0 1 0 1 0 1 1 1 1 11 1 1 1 0 0 1 1 1 0 0 0 1 0 1 1 0 1 1 0 0 1 1 0 0 0 1 0 1 1 1 1 10 0 0 0 11 1 1 0 0 1 0 \\
& 0 1 1 1 0 1 1 0 10 1 1 0 0 0 1 1 0 0 1 1 0 1 1 0 0 0 0 0 0 1 1 10 0 1 1 1 0 1 1 111 1 1 1 1 0 1 0 0 1 0 1 0 10 1 0 1 0 1 1 0 1 1 10 \\
& 1 1 0 0 0 1 1 1 0 1 0 00 1 1 1 1 0 1 0 0 0 0 1 1 1 0 0 1 1 1 1 0 1 0 11 0 0 1 0 1 0 1 0 1 0 0 1 0 1 0 1 1 0 1 0 0 0 01 0 1 10 1 0 0 1 \\
& 0 1 0 1 1 0 1 1 1 1 0 1 1 1 0 0 1 1 1111111 1 0 1 0 0 0 1 1 1 0 1 0 1 1 1 1 0 0 1 0 0 1 1 1 1 0 1 0 1 0 1 0 1 0 0 1 0 01 0 1 0 1 1 \\
&1 0 1 1 1 0 1 1 1 1 1 0 1 1 1 1 0 1 0 1 1 1111 0 1 1 0 0 1 1 1 0 0 1 1 1 0 1 0 1 0 0 1 0 0 0 1 1 0 1 0 1 0 0 0 1 1 0 00 0 1 1 10 1 0 \\
& 0 0 1 0 0 0 0 0 1 1 0 0 0 0 1 1 0
\end{align*}
Al aplicar estos cálculos, Geralt estima que la probabilidad de obtener una desviación así es de aproximadamente 0,01 (lo cual es muy bajo). Se da cuenta de que está enfrentando un fraude y solicita reiniciar el juego utilizando otra moneda, ya que la proporcionada está sesgada.
Se dirige hacia un crupier del casino para obtener una moneda oficial y equilibrada, con el fin de continuar el juego de manera justa y equitativa.

Credit: Netflix
La Intriga de la Ruina del Jugador: La Probabilidad de Perderlo Todo
El juego es equilibrado, lo que significa que cada jugador tiene la misma probabilidad de ganar. Geralt, el sorceleur, está interesado en la probabilidad de que el desconocido quede arruinado antes que él, es decir, que su fortuna final \(F_{\text{Desconocido}}\) llegue a 0 antes de 2000. En términos matemáticos, esta probabilidad se expresa como: \begin{align*} \mathbb{P}_{Desconocido}(1000)=\mathbb{P}_{1000}\left(F\text{ llegue a } 0 \text{ antes de } 2000\right). \end{align*} Esto también se puede expresar utilizando lo que se conoce como «tiempos de detención». Estos son tiempos aleatorios que pueden determinarse a partir de la información disponible sobre el proceso hasta ese momento. Su valor indica el momento en el que se cumple una cierta condición o se alcanza una cierta cantidad. El tiempo de detención puede depender de las realizaciones pasadas del proceso, pero no puede depender del futuro. En nuestro caso, esto puede ser el tiempo (que hemos llamado «manche» en este caso) que denotaremos como \(T_0\) o el tiempo en el que la fortuna del desconocido alcanza 0 o el tiempo \(T_{2000}\) en el que alcanza 2000. En otras palabras, es el tiempo más pequeño n tal que \(F_n\) sea cero o igual a 2000: \begin{align*}T_0=\inf\{n\geq 0,\quad F_n =0\}\quad \text{ et } \quad T_{2000}=\inf\{n\geq 0,\quad F_n =2000\}.\end{align*} Es bastante claro que, cuanto más tiempo se juega, más probabilidades hay de que el juego termine, es decir, que uno de los dos jugadores quede arruinado. Por lo tanto, podemos escribir que la probabilidad de que el desconocido pierda todo su oro antes que Geralt es igual a la probabilidad de que el tiempo de parada \(T_0\) sea menor que \(T_{2000}\): \begin{align*}\mathbb{P}_{Desconocido}(1000)=\mathbb{P}_{1000}\left(T_0<T_{2000}\right).\end{align*} También es importante tener en cuenta que la fortuna del desconocido puede alcanzar todos los posibles «estados» (o su fortuna puede tener cualquier valor entre 0 y 2000), lo que denominaremos como k. Por lo tanto, la probabilidad de que, teniendo una fortuna de valor k, alcance 0 antes de llegar a 2000 es: \begin{align*}\mathbb{P}_{Desconocido}(k)=\mathbb{P}_{k}\left(T_0<T_{2000}\right).\end{align*} Esta probabilidad depende únicamente del valor de la fortuna en la mancha anterior. En efecto, dado que en cada mancha solo se juega una pieza de oro, cada jugador puede ganar o perder solo una pieza y no 4 de una vez, por ejemplo. Sin entrar en detalles y manteniendo generalidades, esto implica que la probabilidad anterior es: \begin{align*} \mathbb{P}_{Desconocido}(k)=p\mathbb{P}_{Desconocido}(k+1)+(1-p)\mathbb{P}_{Desconocido}(k-1). \end{align*} La moneda está equilibrada, por lo que se escribe de la siguiente manera: \begin{align*} \mathbb{P}_{Desconocido}(k)=\frac{1}{2}\mathbb{P}_{Desconocido}(k+1)+\frac{1}{2}\mathbb{P}_{Desconocido}(k-1). \end{align*} Un ojo entrenado resolverá esta ecuación fácilmente y proporcionará una relación explícita de la probabilidad que nos interesa \begin{align*} \mathbb{P}_{Desconocido}(k)=1-\frac{k}{2000}. \end{align*} Entonces, si el desconocido tiene una fortuna de 1000, la probabilidad de que alcance 0 antes que el sorceleur es de: \begin{align*} \mathbb{P}_{Desconocido}(1000)=1-\frac{1000}{2000}=\frac{1}{2}. \end{align*} Por un método similar, también podemos determinar el tiempo promedio para alcanzar 0 antes de 2000, que se denota como \(\mathbb{E}_k(T)\), y vale \begin{align*} \mathbb{E}_k(T)=k(2000-k). \end{align*} Entonces, si \(k=1000\), será necesario jugar en promedio un millón de partidas para que uno de los dos alcance \(0\). El hombre con capucha llama a este intrigante concepto: la ruina del jugador.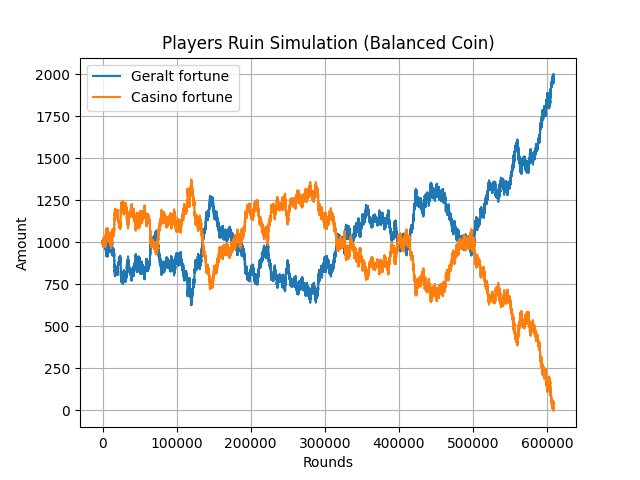
Simulación de la ruina del jugador donde Geralt gana después de aproximadamente 600,000 partidas.

Credit: Netflix
El Secreto del Casino: Sesgo, Engaño y Manipulación de Probabilidades
Después de una feroz batalla, el brujo triunfa sobre su adversario con una gracia incomparable. El rostro enmascarado del desconocido se revela, mostrando una mirada llena de admiración y sorpresa. Con voz temblorosa, revela su verdadera identidad como el poderoso dueño del casino. El brujo queda desconcertado, dándose cuenta de que la fortuna de este hombre supera con creces todas las predicciones que podrían haberse hecho.

Credit: Netflix
En un gesto de generosidad inesperada, el propietario del casino decide compartir algunos de sus secretos con Geralt en una sala apartada, lejos de oídos indiscretos. Le revela que, gracias a su inmensa riqueza, su probabilidad de perder es insignificante, lo que le permite persistir y prosperar en sus emprendimientos. Específica que al nombrar las dos fortunas iniciales como \(F_{Geralt}\) y \(F_{Casino}\), obtiene la siguiente ecuación:
\begin{align*}
\mathbb{P}_{Casino}(k)=1-\frac{k}{F_{Geralt}+F_{Casino}}\quad\text{y}\quad \mathbb{E}_k(T)=k(F_{Geralt}+F_{Casino}-k).
\end{align*}
Con solo tener 100 veces más dinero inicial que Geralt, el casino pierde su fortuna con una probabilidad baja que es de:
\begin{align*}
\mathbb{P}_{Casino}(100\times F_{Geralt})=1-\frac{100\times F_{Geralt}}{F_{Geralt}+100\times F_{Geralt}}=1-\frac{100}{101}=0.0099.
\end{align*}
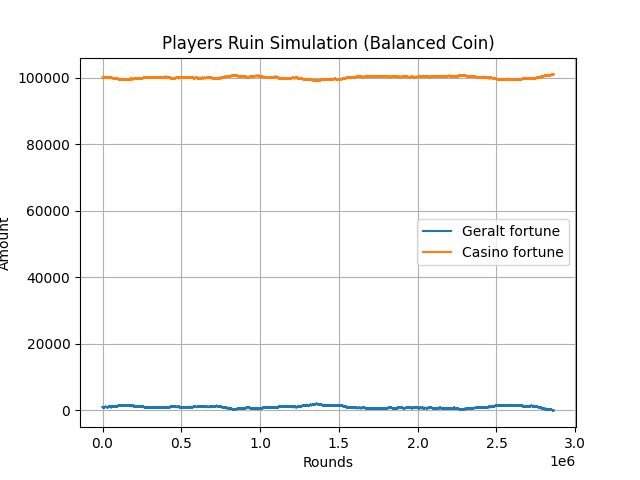

Credit: Netflix
Simulación de la ruina del jugador cuando el casino tiene 100 veces más dinero que Geralt
Pero el secreto más preciado se revela en un susurro apenas audible. El desconocido admite haber jugado con monedas cuidadosamente sesgadas a su favor. Una sonrisa se dibuja en su rostro mientras revela esta inquietante verdad. Esta sutil manipulación le ha permitido aumentar espectacularmente sus ganancias y mantener su control sobre las almas jugadoras que frecuentan su establecimiento. Él le recuerda que, según el sesgo de la moneda, su probabilidad de perder con una fortuna inicial k es de
\begin{align*}
\mathbb{P}_{Casino}(k)=\frac{\left(\frac{1-p}{p}\right)^{F_{Casino}+F_{Geralt}}-\left(\frac{1-p}{p}\right)^{k}}{\left(\frac{1-p}{p}\right)^{F_{Casino}+F_{Geralt}}-1}
\end{align*}
Así que si p está muy cerca de 1, esta probabilidad es muy baja. Además, al observar el esquema proporcionado por el anfitrión, Geralt se da cuenta rápidamente de que incluso con una moneda ligeramente sesgada, estaría destinado a perder.
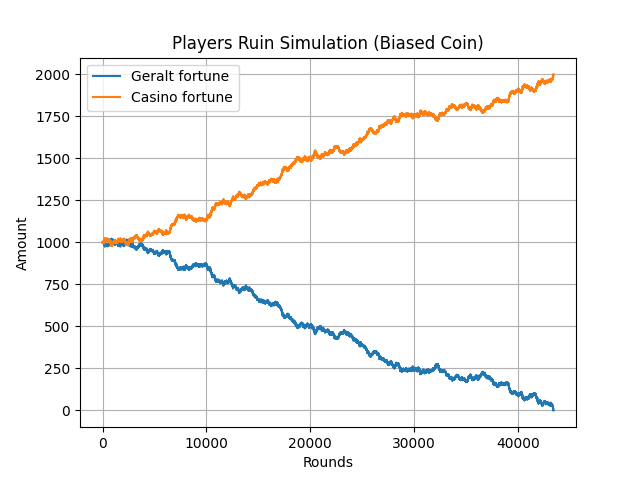

Credit: Netflix
Simulación de la ruina del jugador con una moneda sesgada (\(p=0.49\)).
La Manipulación de los Lanzamientos de Moneda
El poder de la poción de concentración se disipa, y Geralt sale de su trance. Es en este momento que las palabras del famoso mago Persi Diaconis resuenan en la mente del brujo.
Credit: Netflix
La poción de precisión que posee es una creación única en su género. Un solo sorbo de esta poción eleva sus habilidades a un nivel extraordinario, otorgándole un dominio total sobre el lanzamiento de la moneda. Como una máquina, Geralt controla cada aspecto del lanzamiento: las condiciones iniciales, el número de rotaciones realizadas en el aire e incluso el lado que será revelado cuando la moneda caiga. Su precisión en la manipulación de estos parámetros es asombrosa, cuestionando la idea de que el juego del lanzamiento de moneda sea un simple proceso aleatorio.
Esta espectacular demostración de habilidad ilustra perfectamente los descubrimientos del estudio realizado por Joe Keller en nuestra realidad. De hecho, este estudio revela que el lanzamiento de una moneda, aunque pueda parecer aleatorio, está en realidad regido por leyes mecánicas. Cuando se lanza una moneda con una velocidad inicial alta y una fuerte rotación, tiene una probabilidad de caer del mismo lado por el cual comenzó, en casi la mitad de los casos. Sin embargo, si se tiene en cuenta la precesión, es decir, el cambio del eje de rotación de la moneda durante su vuelo, el resultado puede diferir. Si el ángulo entre el momento angular y la normal de la moneda es inferior a 45 grados, la moneda nunca se volteará y siempre caerá del mismo lado.
Gracias a su poción de precisión, Geralt destaca la posibilidad de manipular los lanzamientos de monedas de manera controlada, creando así la ilusión de un juego aleatorio mientras es consciente de que los resultados están determinados en realidad por factores mecánicos. En el centro de esta manipulación se encuentra un elemento crucial: la mano que lanza la moneda no siempre la sostiene del mismo lado, alternando entre águila y sol. Es esta aleatoriedad inconsciente realizada por la persona que lanza la moneda, al colocarla en su pulgar antes de darle un ligero impulso inicial, la que uniformiza las probabilidades de obtener águila o sol. Así, el resultado del lanzamiento tiende hacia la igualdad.

Credit: Netflix
Sin embargo, para aquellos que aspiran a una ligera ventaja, un entrenamiento riguroso en el lanzamiento preciso puede permitirles dominar este arte sutil y hacer que la moneda caiga según sus deseos. Pero, con su ingenio, los juegos de azar introducen otro componente aleatorio: otro jugador debe gritar «Águila» o «Sol» en el preciso momento en que la moneda da vueltas en el aire, escapando así a cualquier predicción.
En esta cautivadora historia, podemos apreciar la importancia de ese equilibrio entre precisión y azar. Geralt de Rivia, a pesar de su extraordinario dominio en el lanzamiento de la moneda gracias a su poción de precisión, comprende que la verdadera esencia del juego reside en esa aleatoriedad inconsciente que asegura la equidad de las probabilidades. El lanzamiento de la moneda sigue siendo un juego fascinante donde la incertidumbre y la magia del momento se entrelazan armoniosamente, despertando en cada uno una curiosidad matizada de misterio.
Revelaciones del Lanzamiento de Monedas: La Intuición de Geralt
En las oscuras sinuosidades de los juegos de azar, donde el destino de las almas jugadoras se decide con un simple lanzamiento de moneda, Geralt de Rivia, el legendario brujo, ha revelado una verdad inquietante. Destaca la importancia de las probabilidades y las herramientas estadísticas para comprender y analizar situaciones aleatorias. A pesar de las apariencias, Geralt se da cuenta de que el juego de la moneda es en realidad un juego de probabilidades y posibilidades. Gracias a su inteligencia y a su poción de concentración, utiliza conceptos como la ley de los grandes números y la desigualdad de concentración gaussiana para evaluar las probabilidades y los riesgos asociados con los lanzamientos de monedas.
Aunque Geralt no puede lanzar la moneda un número infinito de veces, logra obtener estimaciones confiables de la proporción de Águila y Sol utilizando resultados probabilísticos y estadísticos. Su búsqueda también resalta la importancia de la prudencia y el autoconocimiento en los juegos de azar. Al estar consciente de las probabilidades y los riesgos, Geralt toma decisiones informadas y minimiza las consecuencias de sus elecciones.
Así que ya sea que seas un aventurero solitario en los confines del mundo real o un jugador intrépido en los misterios de los casinos, siempre recuerda que detrás del velo de la ilusión se esconde la implacable verdad matemática. Y como Geralt ha comprendido, a veces, la mayor victoria reside en la sabiduría de saber cuándo alejarse de la mesa de juego, dejando atrás los efímeros espejismos para abrazar una realidad más estable. Una que quizás involucre un merecido baño.

Credit: Netflix
Bibliografía
D. Chafaï, F. Malrieu, Recueil de modèles aléatoires, 2015.
T. Bodineaux, Modélisation de phénomènes aléatoires : introduction aux chaînes de Markov et aux martingales, 2015
M. Ledoux, The concentration of measure phenomenon, 2001
I, Stewart, Do dice play god?, 2019
R. Epstein, The Theory of Gambling and Statistical Logic (Revised ed.), 1995
J. L. Coolidge, The Gambler’s Ruin. Annals of Mathematics. 10 (4): 181–192, 1909
import numpy as np
import matplotlib.pyplot as plt
def simulate_biased_coin_tosses(n, p, num_trials):
"""
Simulates multiple trials of biased coin tosses and plots the running average.
Args:
n (int): Number of coin tosses in each trial.
p (float): Probability of getting heads (biased coin).
num_trials (int): Number of trials to simulate.
"""
results = []
for _ in range(num_trials):
coin_tosses = np.random.choice([0, 1], size=n, p=[1-p, p])
running_average = np.cumsum(coin_tosses) / np.arange(1, n + 1)
results.append(running_average)
# Plot the results
for i, running_average in enumerate(results):
plt.plot(np.arange(1, n + 1), running_average, alpha=0.5)
# Plot the theoretical expectation (p for a biased coin)
plt.plot(np.arange(1, n + 1), np.full(n, p), color='red', linestyle='--', label='Theoretical Expectation')
plt.xlabel('Number of Tosses')
plt.ylabel('Running Average')
plt.title('Law of Large Numbers Simulation (Balanced Coin)')
plt.legend()
plt.grid()
plt.show()
# Parameters
n = 100000 # Number of coin tosses in each trial
p = 0.5 # Probability of getting heads (biased coin)
num_trials = 1 # Number of trials to simulate
# Perform the simulation and visualize the results
simulate_biased_coin_tosses(n, p, num_trials)
import numpy as np
import matplotlib.pyplot as plt
def simulate_binomial_distribution(n, p, num_trials):
"""
Simulates multiple trials of a binomial distribution and plots the histogram of outcomes.
Args:
n (int): Number of trials in each binomial experiment.
p (float): Probability of success in each trial.
num_trials (int): Number of trials to simulate.
"""
results = np.random.binomial(n, p, size=num_trials)
# Plot the histogram of outcomes
plt.hist(results, bins=np.arange(n + 1) - 0.5, density=True, alpha=0.7, edgecolor='black')
# Plot the theoretical probability mass function
x = np.arange(n + 1)
y = np.array([np.math.comb(n, k) * p**k * (1 - p)**(n - k) for k in x])
plt.plot(x, y, color='red', label='Theoretical Probability')
plt.xlabel('Number of Successes')
plt.ylabel('Probability')
plt.title(f'Binomial Distribution (n={n}, p={p})')
plt.legend()
plt.grid()
plt.show()
# Parameters
n =10 # Number of trials in each binomial experiment
p = 0.5 # Probability of success in each trial
num_trials = 100000 # Number of trials to simulate
# Perform the simulation and visualize the results
simulate_binomial_distribution(n, p, num_trials)
# Importing libraries
import numpy as np
import pandas as pd
import seaborn as sns
from scipy.stats import norm
import matplotlib.pyplot as plt
# Function to simulate coin toss
def coin_toss(n, deviation):
coin = np.random.choice([0, 1], size=n) # Simulating coin toss
proportion = np.mean(coin) # Calculating proportion of Heads
concentration = 2 * np.exp(-2 * n * deviation**2) # Calculating Gaussian concentration
return proportion, concentration
# Parameters for simulation
n_values = [10, 20, 30, 40, 50, 75, 100, 500, 1000, 10000]
deviation_values = [0.01, 0.03, 0.05, 0.07, 0.1, 0.15, 0.2, 0.25, 0.3, 0.5]
# Simulation and calculation of Gaussian concentration for each combination of parameters
results = []
for n in n_values:
row = []
for deviation in deviation_values:
proportion, concentration = coin_toss(n, deviation)
row.append(concentration)
results.append(row)
# Creating DataFrame from results
df = pd.DataFrame(results, columns=deviation_values, index=n_values)
# Displaying results as a table
print("Number of coin tosses\t", end="")
for deviation in deviation_values:
print(f"Deviation {deviation}\t", end="")
print()
for i, n in enumerate(n_values):
row_str = f"{n}\t\t"
for j, deviation in enumerate(deviation_values):
row_str += f"{results[i][j]:.3e}\t"
print(row_str)
# Creating heatmap with Seaborn
plt.figure(figsize=(12, 8))
sns.heatmap(data=df, annot=True, cmap="Reds", fmt=".2e", cbar=True, cbar_kws={'label': 'Gaussian concentration'})
plt.xlabel("Deviation")
plt.ylabel("Number of coin tosses")
plt.title("Gaussian concentration as a function of the deviation and the number of coin tosses")
plt.show()
# Importing libraries
import numpy as np
import pandas as pd
import seaborn as sns
from scipy.stats import norm
import matplotlib.pyplot as plt
# Function to simulate coin toss
def coin_toss(n, deviation):
coin = np.random.choice([0, 1], size=n) # Simulating coin toss
proportion = np.mean(coin) # Calculating proportion of Heads
concentration = 2 * np.exp(-2 * n * deviation**2) # Calculating Gaussian concentration
return proportion, concentration
# Parameters for simulation
n_values = [10, 20, 30, 40, 100, 500, 1000]
deviation_values = [0.01, 0.03, 0.05, 0.1, 0.2]
# Simulation and calculation of Gaussian concentration for each combination of parameters
results = []
for n in n_values:
row = []
for deviation in deviation_values:
proportion, concentration = coin_toss(n, deviation)
row.append(concentration)
results.append(row)
# Creating DataFrame from results
df = pd.DataFrame(results, columns=deviation_values, index=n_values)
# Displaying results as a table
print("Number of coin tosses\tDeviation 0.01\tDeviation 0.03\tDeviation 0.05\tDeviation 0.1\tDeviation 0.2")
for i, n in enumerate(n_values):
row_str = f"{n}\t\t"
for j, deviation in enumerate(deviation_values):
row_str += f"{results[i][j]:.3e}\t"
print(row_str)
# Creating the graph with Seaborn
sns.set(style="whitegrid")
plt.figure(figsize=(10, 6))
sns.lineplot(data=df, markers=True, dashes=False)
plt.xlabel("Number of coin tosses")
plt.ylabel("Gaussian concentration")
plt.title("Gaussian concentration as a function of the number of coin tosses and the deviation")
plt.legend(title="Deviation")
plt.show()
import numpy as np
import matplotlib.pyplot as plt
def simulate_ruin(player_a_amount, player_b_amount, win_probability):
"""
Simulates the ruin of two players in a gambling game and returns the number of rounds played.
Args:
player_a_amount (int): Initial amount of money for player A.
player_b_amount (int): Initial amount of money for player B.
win_probability (float): Probability of winning a bet.
Returns:
int: Number of rounds played until one of the players goes broke.
"""
rounds = 0
while player_a_amount > 0 and player_b_amount > 0:
# Simulate a round of the game
if np.random.rand() < win_probability:
player_a_amount += 1 # Player A wins
player_b_amount -= 1 # Player B loses
else:
player_a_amount -= 1 # Player A loses
player_b_amount += 1 # Player B wins
rounds += 1
return rounds
def simulate_ruin_visual(player_a_amount, player_b_amount, win_probability):
"""
Simulates the ruin of two players in a gambling game with a biased coin and visualizes the results.
Args:
player_a_amount (int): Initial amount of money for player A.
player_b_amount (int): Initial amount of money for player B.
win_probability (float): Probability of winning a bet.
"""
player_a_history = [player_a_amount]
player_b_history = [player_b_amount]
rounds = 0
while player_a_amount > 0 and player_b_amount > 0:
# Simulate a round of the game with a biased coin
if np.random.rand() < win_probability:
player_a_amount += 1 # Player A wins
player_b_amount -= 1 # Player B loses
else:
player_a_amount -= 1 # Player A loses
player_b_amount += 1 # Player B wins
rounds += 1
player_a_history.append(player_a_amount)
player_b_history.append(player_b_amount)
# Plot the results
plt.plot(player_a_history, label='Geralt fortune')
plt.plot(player_b_history, label='Casino fortune')
plt.xlabel('Rounds')
plt.ylabel('Amount')
plt.title('Players Ruin Simulation (Balanced Coin)')
plt.legend()
plt.grid()
plt.show()
# Parameters
player_a_amount = 1000 # Initial amount of money for player A
player_b_amount = 1000 # Initial amount of money for player B
win_probability = 0.5 # Probability of winning a bet (balanced coin)
# Perform the simulation and get the number of rounds played
rounds_played = simulate_ruin(player_a_amount, player_b_amount, win_probability)
print("Number of rounds played:", rounds_played)
# Perform the simulation and visualize the results
simulate_ruin_visual(player_a_amount, player_b_amount, win_probability)

