Wall-E: Les Fondations de son Intelligence
Episode I
Par Jordan Moles le 2 Septembre, 2023

Dans un monde post-apocalyptique dévasté, où les vestiges de la civilisation humaine sont enfouis sous d’immenses montagnes de déchets, un petit robot solitaire du nom de Wall-E se fraie un chemin à travers ce paysage dystopique. Sa mission : le recyclage méthodique des déchets abandonnés depuis des années. Mais Wall-E ne se contente pas de trier les morceaux de plastique, les plaques de métal et les matières organiques.
À travers ses interactions avec son environnement, ce robot dévoué collecte également une abondance d’informations, analyse des millions de données et apprend de ses expériences pour s’adapter, survivre et accomplir ses tâches avec une efficacité remarquable. Les capacités de ce qui semblait être qu’un simple petite robot collecteur de déchets révèle les prémices d’un domaine en plein essor: l’intelligence artificielle.
L'essence même de l'intelligence artificielle : l'apprentissage
Dans les premiers éclats de son existence, notre petit robot, à l’instar d’un ordinateur, naquit pour plonger dans les abîmes des calculs, ceux qui exigeraient des millions d’années pour trouver une réponse humaine. Les tâches, jadis titanesques pour les âmes terrestres, se dressèrent devant lui, insistant pour qu’il les apprivoise.
Mais dans ses circuits, une transformation allait se jouer. Une transformation qui s’inspira des génies de la science du monde entier. Ils insufflèrent en notre robot une forme unique d’intelligence, une étincelle numérique qui changea la donne. Wall-E, jusque-là une machine, devenait une entité qui apprendrait et prendrait des décisions complexes. C’était l’aube de l’intelligence artificielle, une nouvelle ère technologique.
Face aux défis grandissants, Wall-E montra sa versatilité. Il s’engagea sans effort dans les deux types de situations que l’humanité lui présentait. Dans un cas, il suivait docilement les calculs programmés par les humains, répondant comme une calculatrice répondrait à un simple \(1+1\).
Cependant, il fut confronté à une énigme beaucoup plus complexe : comment différencier les types de déchets qu’il rencontrait ? Comment reconnaître le plastique du métal ou du matériau organique ? Ou plus généralement, comment résoudre un problème donnée sans connaître le calcul requis à sa résolution? C’est ici que l’apprentissage entre en scène, une méthode fascinante que nous appelons le Machine Learning. Une méthode qui ouvre une porte lorsque nous ne savons pas quelle clé utiliser. Le Machine Learning est une clé maîtresse pour une multitude de tâches : reconnaissance d’images, prédictions boursières, estimation de valeurs d’or, détection de failles en cybersécurité et, bien sûr, dans notre cas : le tri de déchets.
Pour doter cet ordinateur d’une intelligence apprenante, des méthodes inspirées de notre propre processus d’apprentissage ont été mises en œuvre. Parmi elles, se distinguent trois approches fondamentales:
• Tout d’abord, l’apprentissage supervisé, qui constitue la pierre angulaire du Machine Learning. À l’instar de notre propre expérience d’acquisition de connaissances, cette méthode guide le petit ordinateur à roulette en lui fournissant des exemples pré-étiquetés. Comme un apprenti avide d’assimiler les savoirs, Wall-E est exposé à des situations où les résultats attendus sont déjà connus. Puis, en observant ces exemples, il parvient peu à peu à généraliser les relations entre les entrées et les sorties, lui permettant ainsi de prendre des décisions et de résoudre des problèmes similaires auxquels il sera plus tard confronté.


• Ensuite, l’apprentissage non supervisé, une forme plus libre et exploratoire de l’intelligence artificielle. Cette méthode permet à l’ordinateur de découvrir de manière autonome des structures et des modèles cachés au sein des données, sans la nécessité d’exemples pré-étiquetés. Tel un explorateur intrépide, Wall-E utilise son analyse sensorielle pour discerner des schémas, regrouper des informations similaires et explorer les nuances de son environnement. À travers cette exploration sans contrainte, il acquiert une compréhension profonde du monde qui l’entoure, révélant ainsi des connaissances insoupçonnées.
• Enfin, l’apprentissage par renforcement, qui s’appuie sur un système de récompenses et de punitions pour guider l’ordinateur dans son apprentissage. À l’instar de nos propres motivations, Wall-E est récompensé lorsqu’il accomplit une tâche avec succès et subit des conséquences négatives en cas d’échec. Ces encouragements et ces sanctions lui permettent d’optimiser ses actions, de prendre des décisions intelligentes et d’affiner ses compétences au fil du temps.

Bébé robot deviendra grand: L’architecture de l’apprentissage supervisé
A la naissance de Wall-E, l’humanité avait déjà tracé son exode vers les confins lointains de l’espace, laissant derrière elle une Terre étouffée sous le poids du dérèglement climatique et de la pollution envahissante. Les équilibres naturels qui avaient depuis si longtemps bercé notre monde avaient flanché, reléguant la planète à une nouvelle réalité. Les cités autrefois rayonnantes de vitalité et d’effervescence n’étaient plus que des vestiges, des témoins silencieux d’une ère désormais révolue.
Cependant, un groupe de scientifiques s’était engagé à rester sur cette terre fatiguée, guidé par une vision audacieuse : instruire ce petit robot plein de potentiel, à différencier les métaux, à trier les plastiques, tout cela en vue d’une mission cruciale – nettoyer et régénérer la planète elle-même.

C’est ainsi que s’amorça une phase d’apprentissage, où les savoirs humains furent transmis à Wall-E. Les scientifiques employèrent une méthode particulière pour guider ce robot apprenti : l’apprentissage supervisé. Cette base fondamentale du Machine Learning offrait à Wall-E la possibilité d’évoluer et de grandir en absorbant des exemples clairement pré-étiquetés.
Les prémices de cette aventure s’articulent autour de ce principe, nous invitant à plonger dans les rouages complexes de l’apprentissage et à découvrir les éléments cruciaux qui l’animent.
1. Le Dataset : Un trésor d'informations
Telle une mine d’or pour Wall-E, le dataset, ou ensemble de données, constitue une collection organisée d’exemples sur lesquels le robot basera son apprentissage. Chaque exemple se compose de diverses variables d’entrée (features) qu’il disposera dans une matrice (une sorte de tableau) et des sorties attendues correspondantes (targets) qu’il disposera dans un vecteur (une colonne). Ces dernières variables sont celles que Wall-E cherchera à prédire.
Par exemple, si nous désirons enseigner à Wall-E à reconnaître des déchets, les caractéristiques spécifiques des objets constitueront les données d’entrée (densité, conductivité thermique, électrique, etc.), et les étiquettes indiquant le type de chaque objet constitueront les sorties attendues (plastique, métallique ou organique). Rien de bien compliqué avec ce petit tableau en exemple contenant 5 échantillons.
| Indice | Densité | Conductivité Electrique (\(S.m^{-1}\)) | Teneur en Carbone | Matériel |
|---|---|---|---|---|
| 1 | 4.5 | \(2.4 \times 10^{6}\) | 0 | Métal |
| 2 | 0.5 | \(10^{-16}\) | 0.5 | Organique |
| 3 | 19.3 | \(41 \times 10^{6}\) | 0 | Métal |
| 4 | 1.1 | \(10^{-16}\) | 0.4 | Organique |
| 5 | 1.2 | \(10^{-14}\) | 0 | Plastique |
| Indice | Pureté | Prix de l'Or |
|---|---|---|
| 1 | 0.374540 | 1224.193388 |
| 2 | 0.950714 | 1483.925567 |
| 3 | 0.731994 | 1360.214557 |
| 4 | 0.598658 | 1284.274057 |
| 5 | 0.156019 | 1004.083221 |
2. Le Modèle et ses Paramètres : L'Architecture de l'Apprentissage
Maintenant, permettez-moi de vous présenter la structure que Wall-E utilisera pour apprendre à partir du jeu de données. Cela sera notre modèle. Imaginez une « boîte noire » comme un dispositif électronique que Wall-E utilise pour traiter l’information et faire des prédictions. Elle est « noire » dans le sens où son fonctionnement interne est quelque peu mystérieux et complexe, du moins du point de vue de Wall-E. À l’intérieur de cette boîte, il y a des engrenages, des leviers et des mécanismes cachés qui transforment les entrées (les données collectées par Wall-E) en sorties (les prédictions faites par Wall-E).
À l’intérieur de cette boîte noire, se trouvent les « paramètres ». Ce sont comme les réglages internes que Wall-E peut ajuster pour améliorer sa capacité à faire des prédictions précises. Imaginez que ce sont les boutons et les molettes secrets que Wall-E peut tourner et appuyer pour rendre la boîte noire plus efficace.
Lorsque nous parlons de « modèle », nous nous référons à une configuration spécifique de cette boîte noire ou à la manière dont chaque pièce interagit avec le reste du système.
L’apprentissage supervisé consiste à ajuster les paramètres de cette boîte noire de manière à ce que les prédictions qu’elle génère soient aussi proches que possible des bonnes réponses (étiquettes) fournies dans l’ensemble de données d’entraînement. En ajustant les paramètres et en observant comment les prédictions changent, Wall-E essaie de comprendre comment cette boîte noire fonctionne réellement et comment l’améliorer.
Ces modèles peuvent être de natures différentes, certains sont linéaires et d’autres sont non linéaires. Commençons par explorer les modèles linéaires :
Modèles Linéaires : La Simplicité dans la Linéarité
Ce sont des représentations mathématiques relativement simples mais puissantes. Ils assument que la relation entre les entrées et les sorties est linéaire, ce qui signifie qu’elle peut être représentée par une droite (ou un plan ou un hyperplan dans un espace multidimensionnel).
Comme mentionné plus haut, les scientifiques n’ont pas simplement limité le robot au simple recyclage de déchets, mais ils lui ont également appris à estimer le prix d’un métal en fonction de sa pureté. En reprenant donc ses données, Wall-E dispose d’un dataset comprenant uniquement k échantillons d’or dont sa pureté sera la caractéristique d’entrée \(x^{(k)}\) et le prix correspondant sera la cible \(y^{(k)}\). Reprenons le tableau précédent pour illustrer cela.
| Indice | x | y |
|---|---|---|
| 1 | 0.374540 | 1224.193388 |
| 2 | 0.950714 | 1483.925567 |
| 3 | 0.731994 | 1360.214557 |
| 4 | 0.598658 | 1284.274057 |
| 5 | 0.156019 | 1004.083221 |
Ici, on a donc 5 échantillons d’or avec leurs données respectives qui nous indique par exemple que l’échantillon 2 possède une pureté \(x^{(2)}=0.731994\) et vaut \(y^{(2)}=1360.214557\) boulons.
On affiche donc sur le graphique les données contenues dans le tableau (on en affiche 50 au lieu de 5 et dites vous qu’il peut y en avoir des millions).


Un tel modèle pourrait donc être représenté par une équation de la forme \(y = ax + b\), où « a » (la pente) et « b » (l’ordonnée à l’origine) sont les paramètres ajustables à l’intérieur de la boîte noire du modèle.
L’apprentissage supervisé vise à trouver les valeurs optimales de « a » et « b » pour que le modèle puisse tracer la meilleure droite possible qui minimise l’erreur entre les prédictions et les valeurs réelles.

Bien sûr, la réalité est plus complexe que cela, et pour une estimation plus précise du prix de l’or, il serait nécessaire de prendre en compte des informations historiques sur les prix de l’or au fil du temps, ainsi que des caractéristiques économiques, politiques et géopolitiques pertinentes qui peuvent influencer sa valeur.
Bien que les modèles linéaires soient simples et faciles à interpréter, ils peuvent être limités dans leur capacité à capturer des relations complexes entre les variables. C’est là que les modèles non-linéaires entrent en scène.
Modèles Non-Linéaires : L'Elégance dans la Complexité

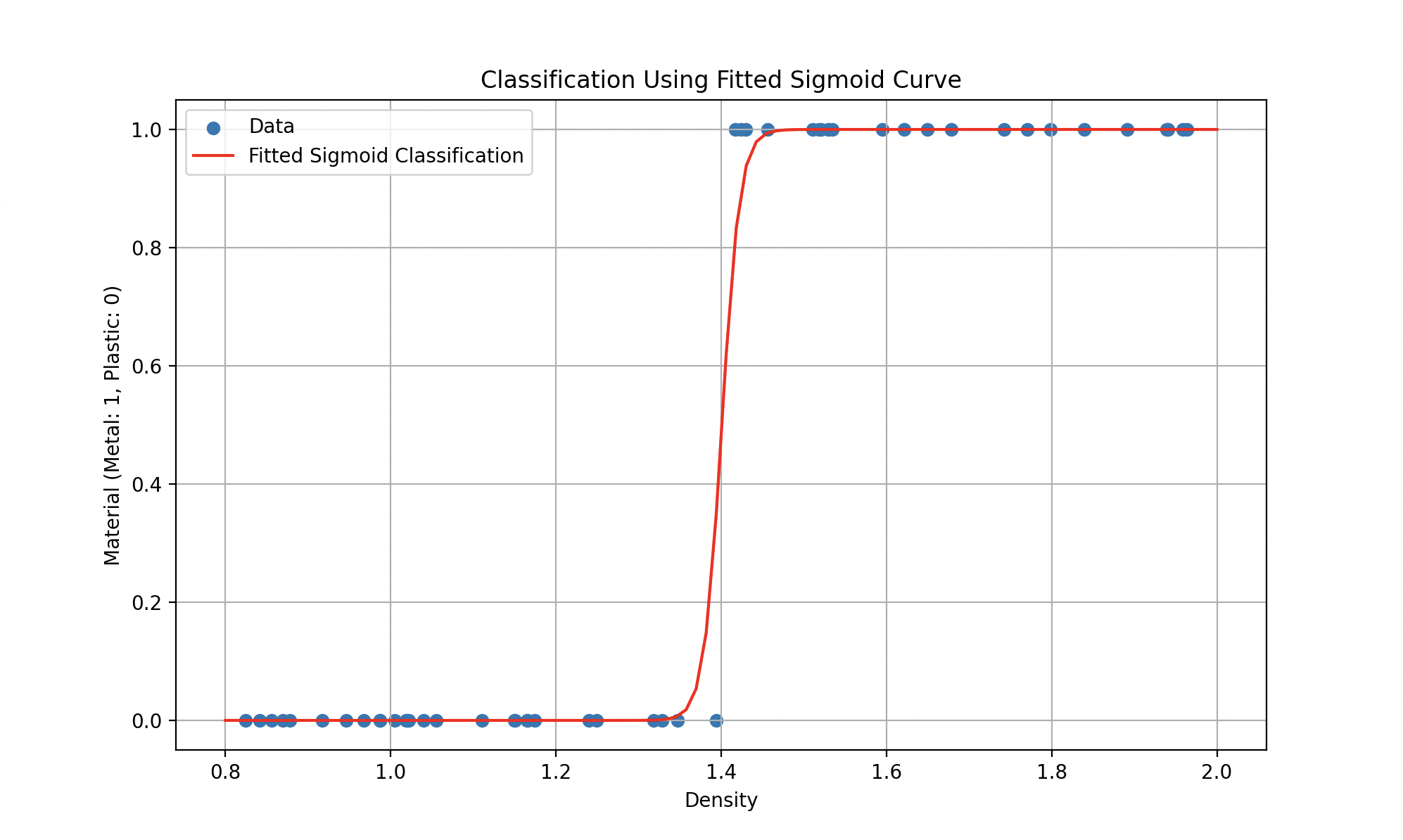

Alors de tels modèles pourrait se représenter plutôt par une équation de la forme \(y = ax^2 + bx +c\) (un polynôme de degré 2 pour la première courbe) ou des fonctions plus compliquées (comme la sigmoïde pour la deuxième) où le but est toujours de trouver les paramètres qui minimisent l’erreur.
Ainsi, le choix entre un modèle linéaire et un modèle non-linéaire dépend de la nature des données et de la complexité du problème à résoudre. Ces premiers sont généralement préférés lorsque les relations entre les variables sont simples et claires, tandis que les modèles non-linéaires sont privilégiés pour des tâches plus complexes et des jeux de données riches en informations.
3. La Fonction Coût : Mesurer les Erreurs
Pour mesurer à quel point Wall-E est bon dans cette tâche d’estimation d’or, nous utilisons une fonction spéciale appelée Fonction Coût. Cette fonction joue un rôle essentiel en quantifiant les erreurs entre les estimations de prix faites par Wall-E et les véritables prix de l’or issus des données historiques. Elle calcule l’erreur pour chaque estimation, puis somme ces erreurs pour former une mesure globale de la performance de Wall-E dans l’estimation du prix de l’or.

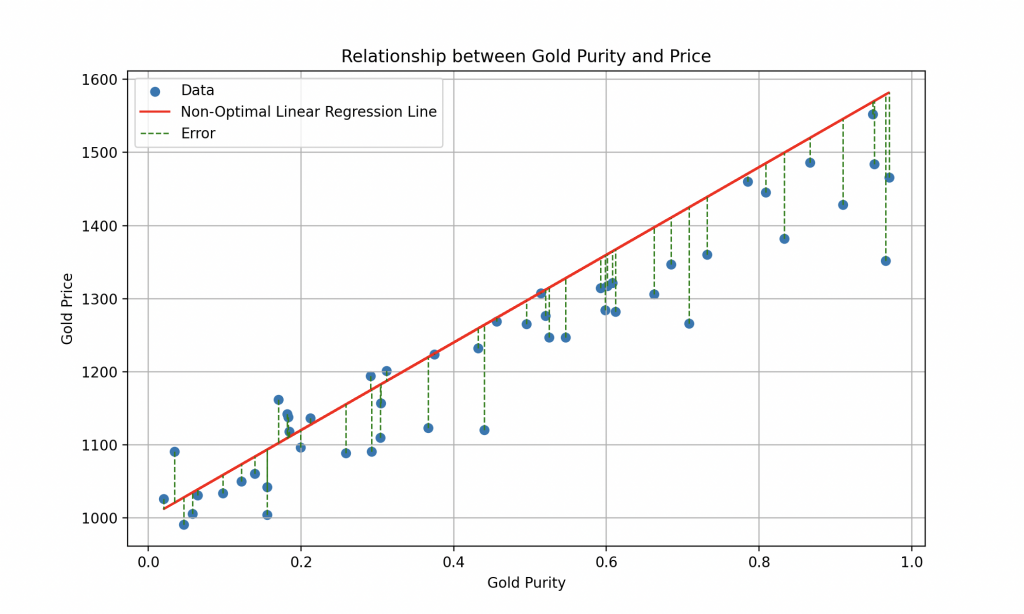
4. L' Algorithme d'Apprentissage : Trouver l'Optimum
Pour parvenir à réduire cette Fonction Coût, Wall-E utilise un algorithme bien connu que l’on appelle la descente de gradient. Cette technique lui permet d’ajuster progressivement ses paramètres internes (pour le modèle linéaire, il ajuste a et b) en fonction des erreurs commises lors de l’estimation des prix de l’or. À chaque étape de l’apprentissage, Wall-E améliore ses performances en se rapprochant de l’optimum, c’est à dire là où la Fonction Coût est minimale.
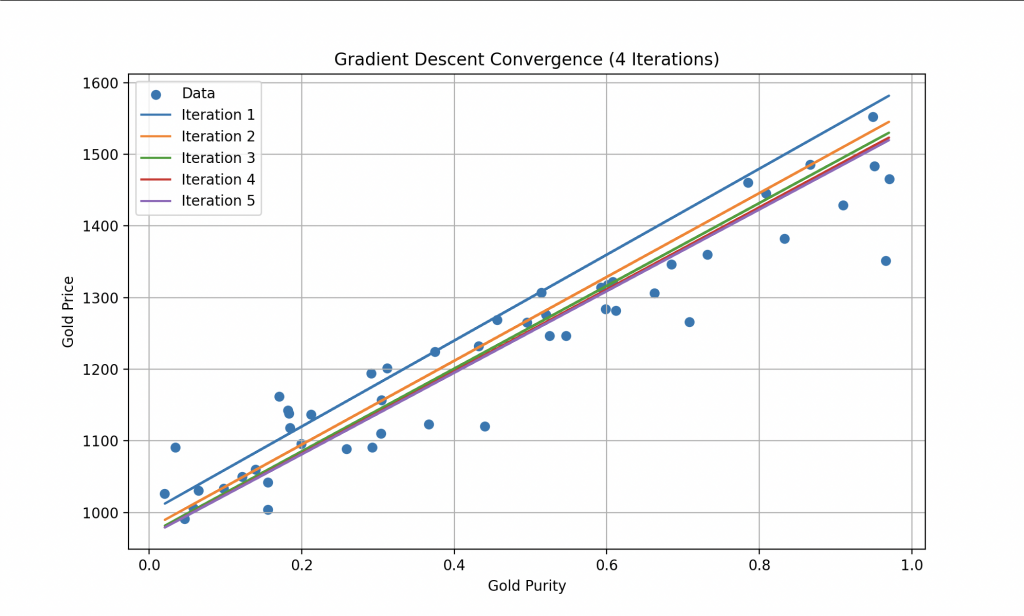

On remarque qu’à chaque itération, les erreurs deviennes de plus en plus faible jusqu’à atteindre une constante. De cette façon, Wall-E devient un expert dans l’estimation du prix de l’or, réalisant ses prédictions avec une précision remarquable.

Ainsi, grâce à la courbe finale, il peut par exemple estimer le prix d’un échantillon d’or avec un taux de pureté de 0.8, ici il vaudrait plus ou moins 1400 boulons.
Un Super Robot
La régression est une technique quantitative utilisée pour prédire des valeurs cibles continues c’est à dire des nombres pouvant prendre n’importe quelle valeur dans un certain intervalle. Ainsi, parmi les passions favorites de Wall-E, l’estimation du prix de l’or fait partie des problèmes de régression. D’autres exemples incluent:
Estimation de la quantité d’eau potable restante: Wall-E peut utiliser des données historiques sur les niveaux d’eau souterraine, les précipitations et les taux d’évaporation pour créer un modèle de régression. Ce modèle pourrait être utilisé pour estimer la quantité d’eau potable restante dans les sources souterraines, permettant ainsi aux humains de mieux planifier leur utilisation de cette ressource vitale.


Prédiction de la production d’énergie solaire: Wall-E dépend de l’énergie solaire pour alimenter ses fonctions et se recharger. En utilisant des données sur l’ensoleillement quotidien, la qualité des panneaux solaires et d’autres facteurs environnementaux, Wall-E pourrait créer un modèle de régression pour prédire la production d’énergie solaire à différents moments de la journée et dans différentes conditions météorologiques.
Estimation de la durée de vie des batteries: Les batteries de Wall-E se dégradent avec le temps et l’utilisation. En analysant les performances passées des batteries et en prenant en compte les conditions environnementales, Wall-E pourrait développer un modèle de régression pour estimer la durée de vie résiduelle des batteries. Cela permettrait de planifier les remplacements de batteries de manière proactive.


Prédiction des niveaux de pollution: Wall-E parcourt les montagnes de déchets et les zones polluées. En collectant des données sur les niveaux de pollution de l’air et de l’eau, ainsi que sur les pratiques de déversement de déchets, il pourrait créer un modèle de régression pour prédire les niveaux futurs de pollution dans différentes régions, aidant ainsi à identifier les zones les plus critiques pour l’assainissement.
La classification est une autre technique d’apprentissage supervisé dite qualitative, c’est à dire qu’elle est utilisée pour prédire des étiquettes ou des catégories discrètes. Donc, dans sa quête pour nettoyer la Terre, Wall-E doit trier une grande variété de déchets. En utilisant des données sur la forme, la taille, la composition, et la dangerosité des déchets, il peut créer un modèle de classification pour les catégoriser automatiquement en différentes classes (plastiques, métaux, matières organiques, déchets toxiques, etc.). Cela l’aiderait à optimiser le processus de recyclage et à contribuer à la préservation de l’environnement. Voici quelques exemples d’applications:
Classification des objets célestes: En se déplaçant à travers l’univers, Wall-E rencontre une multitude d’objets célestes, des astéroïdes aux comètes en passant par les planètes. Il peut donc créer un modèle de classification pour identifier automatiquement les différents objets célestes en fonction de leurs caractéristiques et de leurs trajectoires.


Classification des émotions humaines: Lorsque Wall-E interagit avec les humains, il peut collecter des données sur les expressions faciales, les gestes, et les tonalités vocales et ainsi développer un modèle de classification pour reconnaître les émotions humaines telles que la joie, la tristesse, la peur ou la colère. Cela lui permettrait de mieux comprendre et d’adapter ses interactions avec les êtres humains, rendant ses relations encore plus authentiques.
Classification des signaux extraterrestres: En scrutant les étoiles, Wall-E peut détecter des signaux émanant d’autres civilisations extraterrestres. Pour comprendre ces communications cosmiques, il peut utiliser l’apprentissage supervisé pour créer un modèle de classification capable de distinguer les différents types de signaux, tels que les messages de salutation, les schémas mathématiques, ou les avertissements.

Exploration et Enrichissement
Évoluant dans ce monde complexe, le petit robot solitaire a fait preuve d’une maîtrise inégalée à chaque défi qui se présentait à lui. Son voyage commence modestement en tant que simple collecteur de déchets, mais il évolue pour en faire un expert en estimation de valeur, révélant ainsi les fondations profondes de l’intelligence artificielle. Cette trajectoire singulière met en lumière l’incroyable potentiel de l’apprentissage automatique et des techniques qui l’accompagnent.
L’apprentissage supervisé, véritable clé de voûte de cette intelligence, a permis à Wall-E de transcender les limitations de sa nature de machine et de devenir un apprenant agile. Guidé par des exemples pré-étiquetés, il a su assimiler des connaissances complexes et prendre des décisions judicieuses. Par la suite, il a adopté des modèles linéaires et non-linéaires pour interpréter et prédire les relations au sein des données, se métamorphosant en un maître en estimation de la valeur de l’or et en un trieur de déchets d’élite.
Les sections à venir s’immergent plus en détails dans deux aspects cruciaux de l’apprentissage supervisé:
Partie II : Le Petit Mineur d’Or
Nous plongerons dans le modèle de régression qui a permis à Wall-E d’acquérir une compréhension approfondie de l’estimation de la valeur de l’or. De l’analyse du dataset à la conception du modèle en passant par l’utilisation de la fonction coût et de l’algorithme de descente de gradient, chaque étape sera méthodiquement décortiquée. Nous explorerons les nuances des modèles linéaires et non-linéaires, montrant comment Wall-E a optimisé ses performances pour devenir un maître dans l’art de l’estimation de l’or.
Partie III : Le Spécialiste du Tri
Dans cette partie, nous pénètrerons dans l’univers complexe du tri des déchets, une tâche à la fois cruciale et ardue. Nous détaillerons comment Wall-E a utilisé des modèles de classification pour apprendre à distinguer les différents types de déchets. Du traitement du dataset à la création du modèle de classification, en passant par les défis uniques posés par la diversité des matériaux, nous explorerons comment Wall-E est passé d’un simple trieur de déchets à un expert en recyclage.
Tout comme Wall-E a appris à distinguer le plastique du métal et à estimer la pureté de l’or, l’intelligence artificielle trouve sa place dans des domaines allant de la prédiction de la production d’énergie solaire à la classification des émotions humaines. Le génie de Wall-E reflète ainsi une évolution dans la manière dont l’IA enrichit notre compréhension du monde et améliore nos interactions avec lui.
Le chemin parcouru par Wall-E n’est qu’un prologue. Les algorithmes et les modèles qu’il a embrassés ont créé un précédent pour l’intelligence artificielle, élargissant les horizons de ce que les machines peuvent réaliser. Et tandis que les scientifiques et les ingénieurs continuent à bâtir sur ces bases, l’histoire de Wall-E sert de rappel inspirant : même au milieu des décombres, les déchets peuvent devenir la source précieuse de connaissances et de solutions novatrices.
Bibliographie
G. James, D. Witten, T. Hastie et R. Tibshirani, An Introduction to Statistical Learning, Springer Verlag, coll. « Springer Texts in Statistics », 2013
D. MacKay, Information Theory, Inference, and Learning Algorithms, Cambridge University Press, 2003
T. Mitchell, Machine Learning, 1997
F. Galton, Kinship and Correlation (reprinted 1989), Statistical Science, Institute of Mathematical Statistics, vol. 4, no 2, 1989, p. 80–86
C. Bishop, Pattern Recognition And Machine Learning, Springer, 2006
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
# Random data generation
np.random.seed(42) # To reproduce the same results on each run
n_samples = 50 # Number of samples
purity = np.random.rand(n_samples) # Random purity values between 0 and 1
gold_price = 1000 + 500 * purity + np.random.normal(0, 50, n_samples) # Gold price based on purity
# Creating the data array
data = np.column_stack((purity, gold_price))
# Creating a Pandas DataFrame for the table
df = pd.DataFrame(data, columns=['Purity', 'Gold Price'])
# Calculate a non-optimal linear regression line
x = data[:, 0]
non_optimal_line = 600 * x + 1000
# Creating the plot
plt.figure(figsize=(10, 6))
plt.scatter(data[:, 0], data[:, 1], label='Data')
# Adding the non-optimal linear regression line in red
plt.plot(x, non_optimal_line, color='red', label='Non-Optimal Linear Regression Line')
plt.xlabel('Gold Purity')
plt.ylabel('Gold Price')
plt.title('Relationship between Gold Purity and Price')
plt.grid(True)
plt.show()
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
# Random data generation
np.random.seed(42) # To reproduce the same results on each run
n_samples = 50 # Number of samples
purity = np.random.rand(n_samples) # Random purity values between 0 and 1
gold_price = 1000 + 500 * purity + np.random.normal(0, 50, n_samples) # Gold price based on purity
# Creating the data array
data = np.column_stack((purity, gold_price))
# Creating a Pandas DataFrame for the table
df = pd.DataFrame(data, columns=['Purity', 'Gold Price'])
# Calculate a non-optimal linear regression line
x = data[:, 0]
non_optimal_line = 600 * x + 1000
# Creating the plot
plt.figure(figsize=(10, 6))
plt.scatter(data[:, 0], data[:, 1], label='Data')
# Adding the non-optimal linear regression line in red
plt.plot(x, non_optimal_line, color='red', label='Non-Optimal Linear Regression Line')
# Adding lines indicating errors for each point relative to the non-optimal line
for i in range(n_samples):
plt.plot([x[i], x[i]], [data[i, 1], non_optimal_line[i]], color='green', linestyle='--', linewidth=1)
# Adding a single entry in the legend for the error lines
plt.legend(['Data', 'Non-Optimal Linear Regression Line', 'Error'])
plt.xlabel('Gold Purity')
plt.ylabel('Gold Price')
plt.title('Relationship between Gold Purity and Price')
plt.grid(True)
plt.show()
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
# Define the sigmoid function
def sigmoid(x, a, b):
return 1 / (1 + np.exp(-(a * x + b)))
# Define the gradient descent function for sigmoid
def gradient_descent_sigmoid(X, y, P, learning_rate, n_iterations):
m = len(y)
cost_history = np.zeros(n_iterations)
for i in range(n_iterations):
P = P - learning_rate * (1/m) * X.T.dot(sigmoid(X.dot(P), 1, 0) - y)
cost_history[i] = cost_function_sigmoid(X, y, P)
return P, cost_history
# Define the cost function for sigmoid
def cost_function_sigmoid(X, y, P):
m = len(y)
return -1 / m * np.sum(y * np.log(sigmoid(X.dot(P), 1, 0)) + (1 - y) * np.log(1 - sigmoid(X.dot(P), 1, 0)))
# Random data generation for classification
np.random.seed(42)
n_samples = 50
density = np.random.uniform(0.8, 2.0, n_samples)
threshold = 1.4
material = np.where(density > threshold, 1, 0)
# Creating the design matrix X for classification
X_class = np.column_stack((np.ones(n_samples), density))
# Creating the target vector y for classification
y_class = material.reshape(material.shape[0], 1)
# Initialize P for sigmoid classification
P_class = np.random.randn(2, 1)
# Setting the learning rate and number of iterations for sigmoid classification
learning_rate_class = 0.5
n_iterations_class = 1000000
# Performing gradient descent for sigmoid classification
P_final_class, cost_history_class = gradient_descent_sigmoid(X_class, y_class, P_class, learning_rate_class, n_iterations_class)
# Calculate the sigmoid classification curve
x_range_class = np.linspace(0.8, 2.0, 100)
y_pred_sigmoid_class = sigmoid(x_range_class, P_final_class[1], P_final_class[0])
# Creating the plot for sigmoid classification
plt.figure(figsize=(10, 6))
plt.scatter(density, material, label='Data')
plt.plot(x_range_class, y_pred_sigmoid_class, color='red', label='Fitted Sigmoid Classification')
plt.xlabel('Density')
plt.ylabel('Material (Metal: 1, Plastic: 0)')
plt.title('Classification Using Fitted Sigmoid Curve')
plt.legend()
plt.grid(True)
plt.show()
# Display the fitted parameters and cost history for sigmoid classification
print("Fitted Sigmoid Classification Parameters (a, b):", P_final_class)
plt.plot(range(n_iterations_class), cost_history_class)
plt.xlabel('Number of Iterations')
plt.ylabel('Cost')
plt.title('Cost History during Gradient Descent (Sigmoid Classification)')
plt.show()
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
# Random data generation
np.random.seed(42)
n_samples = 50
purity = np.random.rand(n_samples)
gold_price = 1000 + 500 * purity + np.random.normal(0, 50, n_samples) # Linear model
# Creating the data array
data = np.column_stack((purity, gold_price))
# Creating a Pandas DataFrame for the table
df = pd.DataFrame(data, columns=['Purity', 'Gold Price'])
# Define the linear function
def linear(x, a, b):
return a * x + b
# Define the gradient descent function
def gradient_descent(X, y, P, learning_rate, n_iterations):
m = len(y)
cost_history = np.zeros(n_iterations)
for i in range(n_iterations):
P = P - learning_rate * (1/m) * X.T.dot(X.dot(P) - y)
cost_history[i] = cost_function(X, y, P)
return P, cost_history
# Define the cost function
def cost_function(X, y, P):
m = len(y)
return 1 / (2 * m) * np.sum((X.dot(P) - y) ** 2)
# Creating the design matrix X
X = np.column_stack((np.ones(n_samples), purity))
# Creating the target vector y
y = gold_price.reshape(gold_price.shape[0], 1)
# Initialize P
P = np.random.randn(2, 1)
# Setting the learning rate and number of iterations
learning_rate = 0.1
n_iterations = 1000
# Performing gradient descent
P_final, cost_history = gradient_descent(X, y, P, learning_rate, n_iterations)
# Calculate the linear regression line
x_range = np.linspace(0, 1, 100)
y_pred = linear(x_range, P_final[1], P_final[0])
# Creating the plot
plt.figure(figsize=(10, 6))
plt.scatter(purity, gold_price, label='Data')
plt.plot(x_range, y_pred, color='red', label='Optimal Linear Regression')
plt.xlabel('Gold Purity')
plt.ylabel('Gold Price')
plt.title('Linear Relationship between Gold Purity and Price with Linear Regression')
plt.legend()
plt.grid(True)
plt.show()



