Wall-E: Los Fundamentos de su Inteligencia
Episodio I
PorJordan Moles el 2 de Septiembre, 2023

En un mundo postapocalíptico devastado, donde los vestigios de la civilización humana están sepultados bajo inmensas montañas de desechos, un pequeño robot solitario llamado Wall-E abre paso a través de este paisaje distópico. Su misión: el reciclaje metódico de los desechos abandonados durante años. Pero Wall-E no se limita a clasificar trozos de plástico, láminas de metal y materia orgánica.
A través de sus interacciones con el entorno, este robot dedicado también recopila una abundancia de información, analiza millones de datos y aprende de sus experiencias para adaptarse, sobrevivir y llevar a cabo sus tareas con una eficiencia notable. Las capacidades de lo que parecía ser simplemente un pequeño robot recolector de desechos revelan los comienzos de un campo en auge: la inteligencia artificial.
La esencia misma de la inteligencia artificial: el aprendizaje.
En los primeros destellos de su existencia, nuestro pequeño robot, al igual que una computadora, nació para sumergirse en las profundidades de los cálculos, aquellos que requerirían millones de años para encontrar una respuesta humana. Las tareas que una vez fueron titánicas para las almas terrestres se alzaron ante él, insistiendo en que las domara.
Pero en sus circuitos, se estaba gestando una transformación. Una transformación que tomó inspiración de los genios de la ciencia de todo el mundo. Infundieron en nuestro robot una forma única de inteligencia, una chispa digital que cambió el juego. Wall-E, hasta entonces una máquina, se convirtió en una entidad que aprendería y tomaría decisiones complejas. Era el amanecer de la inteligencia artificial, una nueva era tecnológica.
Frente a los crecientes desafíos, Wall-E demostró su versatilidad. Se sumergió sin esfuerzo en los dos tipos de situaciones que la humanidad le presentaba. En un caso, seguía obedientemente los cálculos programados por los humanos, respondiendo como una calculadora respondería a un simple \(1+1\).
Sin embargo, se enfrentó a un enigma mucho más complejo: ¿cómo diferenciar los tipos de desechos que encontraba? ¿Cómo reconocer el plástico del metal o del material orgánico? O más generalmente, ¿cómo resolver un problema dado sin conocer el cálculo requerido para su solución? Aquí es donde entra en juego el aprendizaje, un método fascinante que llamamos Machine Learning. Un método que abre una puerta cuando no sabemos qué llave usar. El Machine Learning es una llave maestra para una multitud de tareas: reconocimiento de imágenes, predicciones bursátiles, estimación de valores del oro, detección de vulnerabilidades en ciberseguridad y, por supuesto, en nuestro caso: la clasificación de desechos.
Para dotar a esta computadora de una inteligencia que aprende, se implementaron métodos inspirados en nuestro propio proceso de aprendizaje. Entre ellos, destacan tres enfoques fundamentales:



El Bebé Robot Crecerá: La Arquitectura del Aprendizaje Supervisado
Al Nacimiento de Wall-E, la humanidad ya había trazado su éxodo hacia los confines lejanos del espacio, dejando atrás una Tierra sofocada bajo el peso del cambio climático y la contaminación invasiva. Los equilibrios naturales que habían acunado a nuestro mundo durante tanto tiempo se habían desmoronado, relegando al planeta a una nueva realidad. Las ciudades una vez radiantes de vitalidad y efervescencia no eran más que vestigios, testigos silenciosos de una era ya pasada.
Sin embargo, un grupo de científicos se comprometió a quedarse en esta tierra cansada, guiados por una visión audaz: instruir a este pequeño robot lleno de potencial para que diferenciara los metales, clasificara los plásticos, todo ello con una misión crucial en mente: limpiar y regenerar el propio planeta.

1. El Dataset: Un Tesoro de Información
Como una mina de oro para Wall-E, el conjunto de datos, o dataset, es una colección organizada de ejemplos en los cuales el robot basará su aprendizaje. Cada ejemplo consta de diversas variables de entrada (features) que se presentarán en una matriz (algo similar a una tabla) y las salidas esperadas correspondientes (targets) que se presentarán en un vector (una columna). Estas últimas variables son las que Wall-E intentará predecir.
Por ejemplo, si deseamos enseñar a Wall-E a reconocer desechos, las características específicas de los objetos constituirán los datos de entrada (densidad, conductividad térmica, eléctrica, etc.), y las etiquetas que indican el tipo de cada objeto constituirán las salidas esperadas (plástico, metálico u orgánico). Nada complicado con este pequeño ejemplo de tabla que contiene 5 muestras.
| Indice | Densidad | Conductividad Eléctrica (\(S.m^{-1}\)) | Tasa de Carbono | Materia |
|---|---|---|---|---|
| 1 | 4.5 | \(2.4 \times 10^{6}\) | 0 | Metal |
| 2 | 0.5 | \(10^{-16}\) | 0.5 | Orgánico |
| 3 | 19.3 | \(41 \times 10^{6}\) | 0 | Metal |
| 4 | 1.1 | \(10^{-16}\) | 0.4 | Orgánico |
| 5 | 1.2 | \(10^{-14}\) | 0 | Plástico |
Por supuesto, como un robot encargado de clasificar basura, esta tarea es su principal misión. Pero nuestro pequeño robot también se apasiona por estimar el precio de los metales, especialmente el del oro. Sin embargo, como no comprende realmente el sistema monetario humano, convierte todo en tornillos.
Por lo tanto, para entretenerlo, los científicos le hacen analizar cada trozo de metal dorado para determinar su pureza y le dan su valor de mercado. Aquí tienes un ejemplo ilustrativo con 5 variables.
| Indice | Pureza | Precio del Oro |
|---|---|---|
| 1 | 0.374540 | 1224.193388 |
| 2 | 0.950714 | 1483.925567 |
| 3 | 0.731994 | 1360.214557 |
| 4 | 0.598658 | 1284.274057 |
| 5 | 0.156019 | 1004.083221 |
2. El Modelo y sus Parámetros: La Arquitectura del Aprendizaje
Ahora, introduzcamos la estructura que Wall-E utilizará para aprender a partir del conjunto de datos. Esto será nuestro modelo. Imagina una «caja negra» como un dispositivo electrónico que Wall-E utiliza para procesar información y hacer predicciones. Es «negra» en el sentido de que su funcionamiento interno es algo misterioso y complejo, al menos desde el punto de vista de Wall-E. Dentro de esta caja, hay engranajes, palancas y mecanismos ocultos que transforman las entradas (los datos que Wall-E recopila) en salidas (las predicciones que Wall-E hace).
Dentro de esta caja negra, se encuentran los «parámetros». Estos son como los ajustes internos que Wall-E puede cambiar para mejorar su capacidad de hacer predicciones precisas. Imagina que son las perillas y botones secretos que Wall-E puede girar y presionar para hacer que la caja negra funcione de manera más efectiva.
Ahora, cuando hablamos de «modelo», nos referimos a una configuración específica de esta caja negra o como cada pieza interactúa con el resto del sistema.
El aprendizaje supervisado consiste en ajustar los parámetros de esta caja negra de manera que las predicciones que hace sean lo más cercanas posible a las respuestas correctas (etiquetas) que se proporcionan en el conjunto de datos de entrenamiento. A medida que ajusta los parámetros y observa cómo cambian las predicciones, Wall-E está tratando de descubrir cómo funciona realmente esta caja negra y cómo hacerla funcionar mejor.
Estos modelos pueden ser de diferentes naturalezas, algunos son lineales y otros no lineales. Comencemos explorando los modelos lineales:
Modelos Lineales: La Simplicidad en la Linealidad
Los modelos lineales son representaciones matemáticas relativamente simples pero poderosas. Suponen que la relación entre las entradas y las salidas es lineal, lo que significa que puede ser representada por una línea (o un plano o un hiperplano en un espacio multidimensional).
Como se mencionó anteriormente, los científicos no limitaron al robot simplemente a reciclar basura, sino que también le enseñaron a estimar el precio de un metal en función de su pureza. Tomando sus datos nuevamente, Wall-E tiene un conjunto de datos que solo incluye k muestras de oro, donde su pureza es la característica de entrada \(x^{(k)}\) y el precio correspondiente es el objetivo \(y^{(k)}\). Retomemos la tabla anterior para ilustrar esto.
| Indice | x | y |
|---|---|---|
| 1 | 0.374540 | 1224.193388 |
| 2 | 0.950714 | 1483.925567 |
| 3 | 0.731994 | 1360.214557 |
| 4 | 0.598658 | 1284.274057 |
| 5 | 0.156019 | 1004.083221 |


Un modelo como este podría representarse con una ecuación en la forma \(y = ax + b\), donde «a» (la pendiente) y «b» (la ordenada al origen) son parámetros ajustables dentro de la caja negra del modelo.
El aprendizaje supervisado tiene como objetivo encontrar los valores óptimos de «a» y «b» para que el modelo pueda trazar la mejor línea posible que minimice el error entre las predicciones y los valores reales.
El gráfico adjunto representa el modelo lineal con «a» y «b» tomados al azar.
Por supuesto, la realidad es más compleja que eso, y para una estimación más precisa del precio del oro, sería necesario considerar información histórica sobre los precios del oro a lo largo del tiempo, así como características económicas, políticas y geopolíticas relevantes que puedan influir en su valor.
Aunque los modelos lineales son simples y fáciles de interpretar, pueden ser limitados en su capacidad para capturar relaciones complejas entre variables. Ahí es donde entran en juego los modelos no lineales.
Modelos No Lineales: La Elegancia en la Complejidad

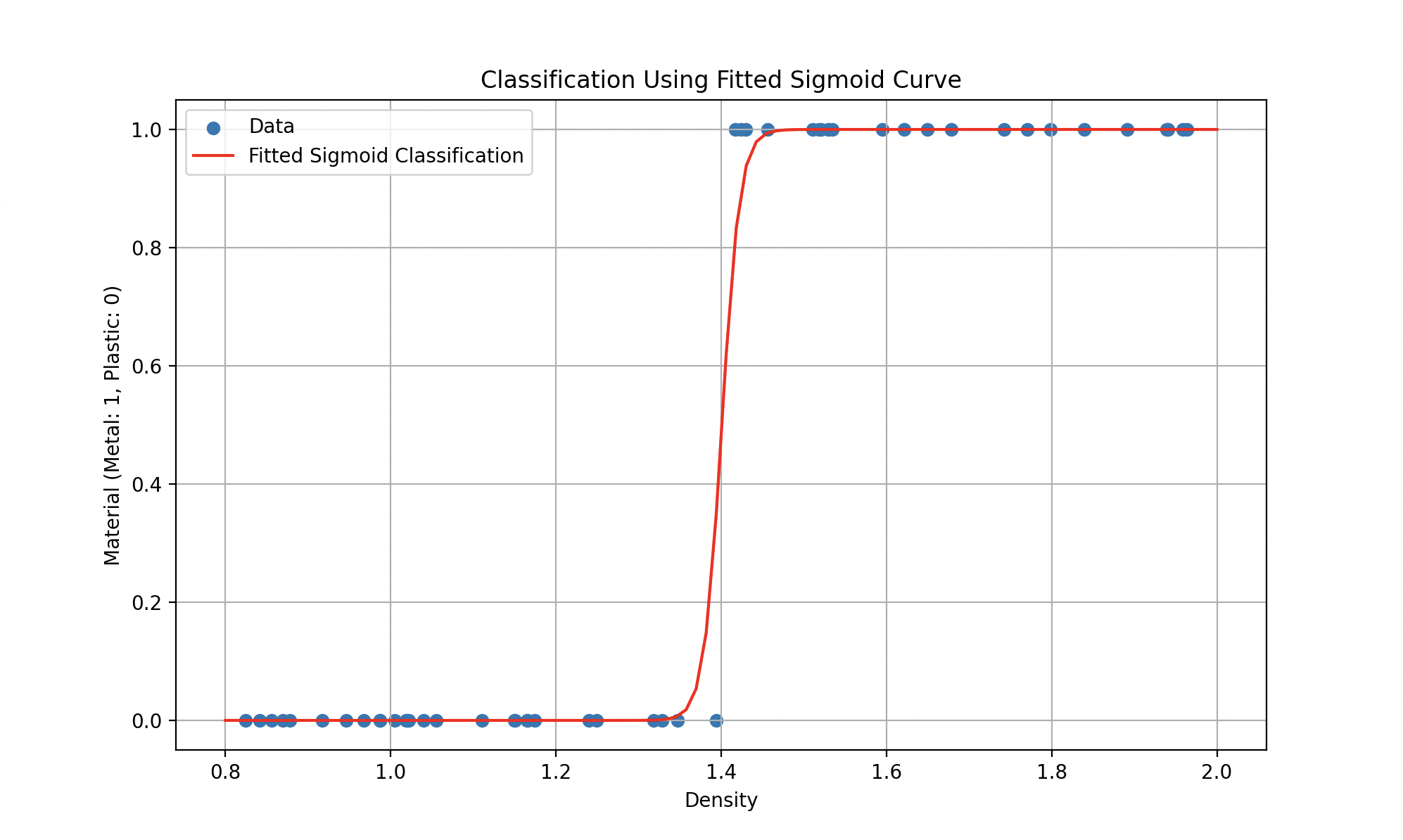

Entonces, tales modelos podrían representarse más bien con una ecuación en la forma \(y = ax^2 + bx +c\) (un polinomio de grado 2 para la primera curva) o funciones más complicadas (como la sigmoidal para la segunda), donde el objetivo sigue siendo encontrar los parámetros que minimicen el error.
Por lo tanto, la elección entre un modelo lineal y un modelo no lineal depende de la naturaleza de los datos y de la complejidad del problema a resolver. Los primeros suelen ser preferidos cuando las relaciones entre las variables son simples y claras, mientras que los modelos no lineales se favorecen para tareas más complejas y conjuntos de datos ricos en información.
3. La Función de Costo: Medir los Errores

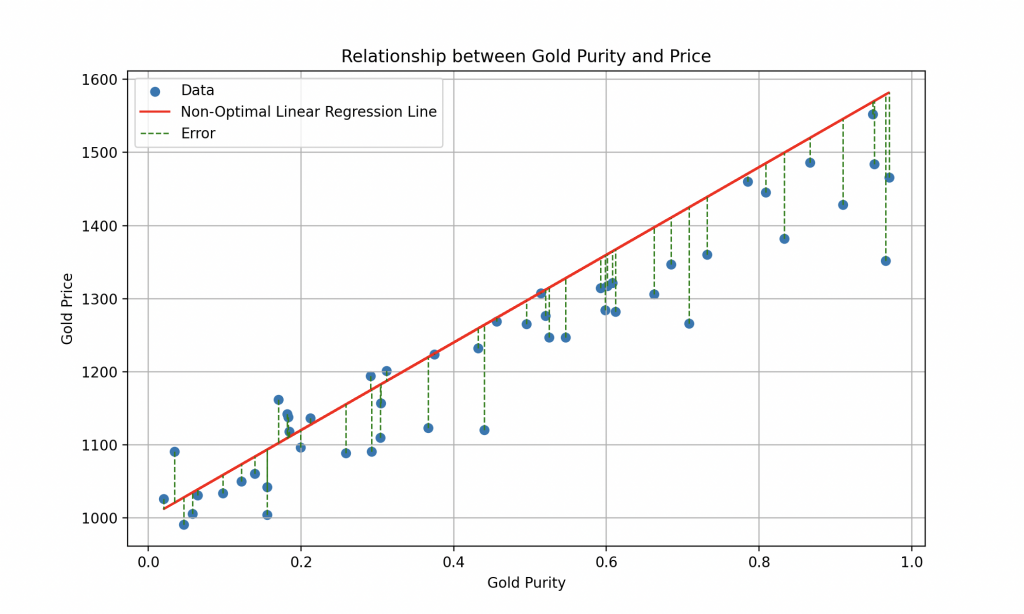
4. El Algoritmo de Aprendizaje: Encontrar el Óptimo
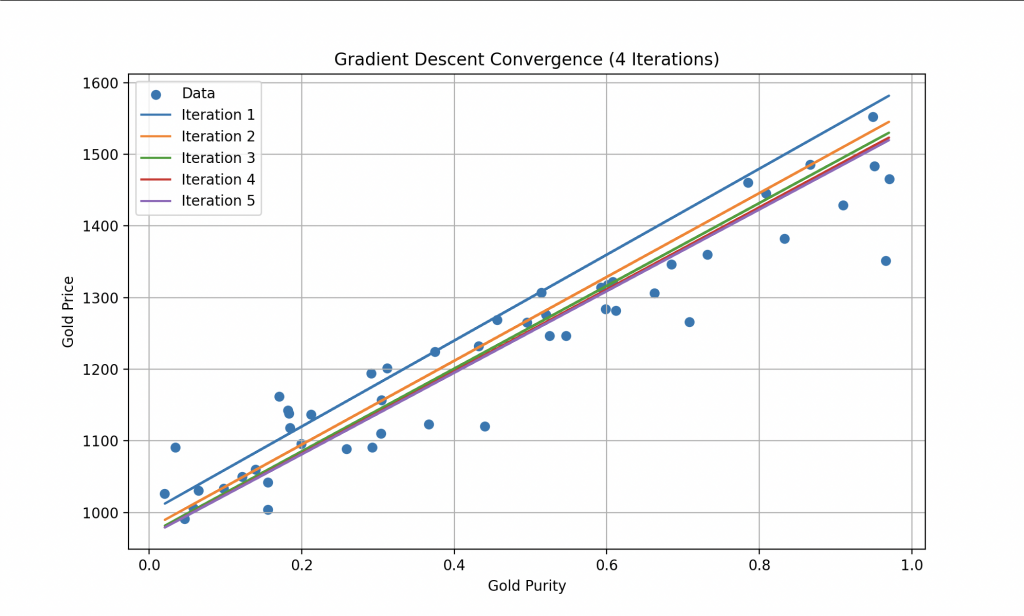


Un Super Robot







Exploración y Enriquecimiento
Evolucionando en este complejo mundo, el pequeño robot solitario demostró una maestría incomparable ante cada desafío que se presentaba. Su viaje comenzó modestamente como un simple recolector de basura, pero evolucionó para convertirse en un experto en estimación de valores, revelando así los cimientos profundos de la inteligencia artificial. Esta trayectoria singular destaca el increíble potencial del aprendizaje automático y las técnicas que lo acompañan.
El aprendizaje supervisado, verdadera piedra angular de esta inteligencia, permitió a Wall-E trascender las limitaciones de su naturaleza de máquina y convertirse en un aprendiz ágil. Guiado por ejemplos preetiquetados, logró asimilar conocimientos complejos y tomar decisiones sabias. Luego, adoptó modelos lineales y no lineales para interpretar y predecir relaciones dentro de los datos, transformándose en un maestro en la estimación del valor del oro y en un experto en clasificación de desechos.
Las secciones siguientes se sumergen en dos aspectos cruciales del aprendizaje supervisado:
Parte II: El Pequeño Minero de Oro
Profundizaremos en el modelo de regresión que permitió a Wall-E adquirir una comprensión profunda de la estimación del valor del oro. Desde el análisis del conjunto de datos hasta el diseño del modelo, pasando por el uso de la función de costo y el algoritmo de descenso de gradiente, cada paso se desglosará meticulosamente. Exploraremos las sutilezas de los modelos lineales y no lineales, mostrando cómo Wall-E optimizó su rendimiento para convertirse en un maestro en el arte de la estimación del oro.
Parte III: El Especialista en Clasificación
En esta parte, nos adentraremos en el complejo universo de la clasificación de desechos, una tarea tanto crucial como desafiante. Detallaremos cómo Wall-E utilizó modelos de clasificación para aprender a distinguir los diferentes tipos de desechos. Desde el procesamiento del conjunto de datos hasta la creación del modelo de clasificación, pasando por los desafíos únicos que plantea la diversidad de materiales, exploraremos cómo Wall-E pasó de ser un simple recolector de basura a convertirse en un experto en reciclaje.
Al igual que Wall-E aprendió a distinguir el plástico del metal y a estimar la pureza del oro, la inteligencia artificial encuentra su lugar en campos que van desde la predicción de la producción de energía solar hasta la clasificación de las emociones humanas. El ingenio de Wall-E refleja así una evolución en la forma en que la IA enriquece nuestra comprensión del mundo y mejora nuestras interacciones con él.
El camino recorrido por Wall-E es solo un prólogo. Los algoritmos y modelos que abrazó han establecido un precedente para la inteligencia artificial, ampliando los horizontes de lo que las máquinas pueden lograr. Y mientras los científicos e ingenieros continúan construyendo sobre estas bases, la historia de Wall-E sirve como un recordatorio inspirador: incluso en medio de los escombros, los desechos pueden convertirse en una valiosa fuente de conocimiento y soluciones innovadoras.
Bibliografía
G. James, D. Witten, T. Hastie et R. Tibshirani, An Introduction to Statistical Learning, Springer Verlag, coll. « Springer Texts in Statistics », 2013
D. MacKay, Information Theory, Inference, and Learning Algorithms, Cambridge University Press, 2003
T. Mitchell, Machine Learning, 1997
F. Galton, Kinship and Correlation (reprinted 1989), Statistical Science, Institute of Mathematical Statistics, vol. 4, no 2, 1989, p. 80–86
C. Bishop, Pattern Recognition And Machine Learning, Springer, 2006
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
# Random data generation
np.random.seed(42) # To reproduce the same results on each run
n_samples = 50 # Number of samples
purity = np.random.rand(n_samples) # Random purity values between 0 and 1
gold_price = 1000 + 500 * purity + np.random.normal(0, 50, n_samples) # Gold price based on purity
# Creating the data array
data = np.column_stack((purity, gold_price))
# Creating a Pandas DataFrame for the table
df = pd.DataFrame(data, columns=['Purity', 'Gold Price'])
# Calculate a non-optimal linear regression line
x = data[:, 0]
non_optimal_line = 600 * x + 1000
# Creating the plot
plt.figure(figsize=(10, 6))
plt.scatter(data[:, 0], data[:, 1], label='Data')
# Adding the non-optimal linear regression line in red
plt.plot(x, non_optimal_line, color='red', label='Non-Optimal Linear Regression Line')
plt.xlabel('Gold Purity')
plt.ylabel('Gold Price')
plt.title('Relationship between Gold Purity and Price')
plt.grid(True)
plt.show()
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
# Random data generation
np.random.seed(42) # To reproduce the same results on each run
n_samples = 50 # Number of samples
purity = np.random.rand(n_samples) # Random purity values between 0 and 1
gold_price = 1000 + 500 * purity + np.random.normal(0, 50, n_samples) # Gold price based on purity
# Creating the data array
data = np.column_stack((purity, gold_price))
# Creating a Pandas DataFrame for the table
df = pd.DataFrame(data, columns=['Purity', 'Gold Price'])
# Calculate a non-optimal linear regression line
x = data[:, 0]
non_optimal_line = 600 * x + 1000
# Creating the plot
plt.figure(figsize=(10, 6))
plt.scatter(data[:, 0], data[:, 1], label='Data')
# Adding the non-optimal linear regression line in red
plt.plot(x, non_optimal_line, color='red', label='Non-Optimal Linear Regression Line')
# Adding lines indicating errors for each point relative to the non-optimal line
for i in range(n_samples):
plt.plot([x[i], x[i]], [data[i, 1], non_optimal_line[i]], color='green', linestyle='--', linewidth=1)
# Adding a single entry in the legend for the error lines
plt.legend(['Data', 'Non-Optimal Linear Regression Line', 'Error'])
plt.xlabel('Gold Purity')
plt.ylabel('Gold Price')
plt.title('Relationship between Gold Purity and Price')
plt.grid(True)
plt.show()
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
# Define the sigmoid function
def sigmoid(x, a, b):
return 1 / (1 + np.exp(-(a * x + b)))
# Define the gradient descent function for sigmoid
def gradient_descent_sigmoid(X, y, P, learning_rate, n_iterations):
m = len(y)
cost_history = np.zeros(n_iterations)
for i in range(n_iterations):
P = P - learning_rate * (1/m) * X.T.dot(sigmoid(X.dot(P), 1, 0) - y)
cost_history[i] = cost_function_sigmoid(X, y, P)
return P, cost_history
# Define the cost function for sigmoid
def cost_function_sigmoid(X, y, P):
m = len(y)
return -1 / m * np.sum(y * np.log(sigmoid(X.dot(P), 1, 0)) + (1 - y) * np.log(1 - sigmoid(X.dot(P), 1, 0)))
# Random data generation for classification
np.random.seed(42)
n_samples = 50
density = np.random.uniform(0.8, 2.0, n_samples)
threshold = 1.4
material = np.where(density > threshold, 1, 0)
# Creating the design matrix X for classification
X_class = np.column_stack((np.ones(n_samples), density))
# Creating the target vector y for classification
y_class = material.reshape(material.shape[0], 1)
# Initialize P for sigmoid classification
P_class = np.random.randn(2, 1)
# Setting the learning rate and number of iterations for sigmoid classification
learning_rate_class = 0.5
n_iterations_class = 1000000
# Performing gradient descent for sigmoid classification
P_final_class, cost_history_class = gradient_descent_sigmoid(X_class, y_class, P_class, learning_rate_class, n_iterations_class)
# Calculate the sigmoid classification curve
x_range_class = np.linspace(0.8, 2.0, 100)
y_pred_sigmoid_class = sigmoid(x_range_class, P_final_class[1], P_final_class[0])
# Creating the plot for sigmoid classification
plt.figure(figsize=(10, 6))
plt.scatter(density, material, label='Data')
plt.plot(x_range_class, y_pred_sigmoid_class, color='red', label='Fitted Sigmoid Classification')
plt.xlabel('Density')
plt.ylabel('Material (Metal: 1, Plastic: 0)')
plt.title('Classification Using Fitted Sigmoid Curve')
plt.legend()
plt.grid(True)
plt.show()
# Display the fitted parameters and cost history for sigmoid classification
print("Fitted Sigmoid Classification Parameters (a, b):", P_final_class)
plt.plot(range(n_iterations_class), cost_history_class)
plt.xlabel('Number of Iterations')
plt.ylabel('Cost')
plt.title('Cost History during Gradient Descent (Sigmoid Classification)')
plt.show()
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
# Random data generation
np.random.seed(42)
n_samples = 50
purity = np.random.rand(n_samples)
gold_price = 1000 + 500 * purity + np.random.normal(0, 50, n_samples) # Linear model
# Creating the data array
data = np.column_stack((purity, gold_price))
# Creating a Pandas DataFrame for the table
df = pd.DataFrame(data, columns=['Purity', 'Gold Price'])
# Define the linear function
def linear(x, a, b):
return a * x + b
# Define the gradient descent function
def gradient_descent(X, y, P, learning_rate, n_iterations):
m = len(y)
cost_history = np.zeros(n_iterations)
for i in range(n_iterations):
P = P - learning_rate * (1/m) * X.T.dot(X.dot(P) - y)
cost_history[i] = cost_function(X, y, P)
return P, cost_history
# Define the cost function
def cost_function(X, y, P):
m = len(y)
return 1 / (2 * m) * np.sum((X.dot(P) - y) ** 2)
# Creating the design matrix X
X = np.column_stack((np.ones(n_samples), purity))
# Creating the target vector y
y = gold_price.reshape(gold_price.shape[0], 1)
# Initialize P
P = np.random.randn(2, 1)
# Setting the learning rate and number of iterations
learning_rate = 0.1
n_iterations = 1000
# Performing gradient descent
P_final, cost_history = gradient_descent(X, y, P, learning_rate, n_iterations)
# Calculate the linear regression line
x_range = np.linspace(0, 1, 100)
y_pred = linear(x_range, P_final[1], P_final[0])
# Creating the plot
plt.figure(figsize=(10, 6))
plt.scatter(purity, gold_price, label='Data')
plt.plot(x_range, y_pred, color='red', label='Optimal Linear Regression')
plt.xlabel('Gold Purity')
plt.ylabel('Gold Price')
plt.title('Linear Relationship between Gold Purity and Price with Linear Regression')
plt.legend()
plt.grid(True)
plt.show()



