Ladrón: (susurrando) Tengo un mal presentimiento acerca de esa palanca. No sabemos lo que podría desencadenar.
Ranger: (cauteloso) Tienes razón; en esta situación, la prudencia es necesaria. No toquemos esa palanca sin más información.
Así que deciden no tocar la palanca por ahora, optando por no arriesgarse a una reacción impredecible. Sin embargo, en ese mismo momento, el tiempo parece congelarse a su alrededor y la entidad luminosa en la jaula de vidrio comienza a hablar.
Azar: (con una voz etérea) Han demostrado sabiduría al evitar la palanca, pero el tiempo apremia. Un equipo de soldados se acerca, liderado por un poderoso mago. Para vencer a estos enemigos, deberán comprender las complejidades de la distribución de probabilidad multinomial.
La Ley de las Monedas
El Divino Azar se alzó, con sus palabras llenas de sabiduría, para iluminar a los aventureros sobre la distribución binomial, una ley fundamental en la probabilidad.

Él explicó que la distribución binomial se basa en n elecciones binarias independientes, muy parecidas a lanzar una moneda n veces, donde los dos posibles resultados son Águila o Sol (n puede ser cualquier número, como 1, 12, 100, etc.). En el caso de una moneda justa, la probabilidad de Águila, denotada como \(p_1\) era 0.5, mientras que la probabilidad de Sol, denotada como \(p_2\) (or \(1-p_1\)), era también 0.5. Además, señaló que si la moneda estuviera sesgada, estas probabilidades (\(p_1\) y \(p_2\)) podrían tomar otros valores, como 0.4 o 0.6, revelando un desequilibrio (ver el artículo Toss a Coin to Your Witcher).
En términos matemáticos, la distribución binomial es una distribución de probabilidad discreta descrita por dos parámetros: el número de ensayos n (o el número de experimentos realizados) y la de éxito \(p_1\) (también podría ser \(p_2\)).
Azar continuó su presentación al introducir la fórmula para calcular la probabilidad de obtener exactamente \(n_1\) Cruces y \(n_2\) Caras en una serie de n ensayos. Se veía así:
\begin{equation*}\mathbb{P}(N_1 = n_1, N_2 = n_2) =\frac{n!}{n_1!n_2!} \cdot p_1^{n_1} \cdot p_2^{n_2}\end{equation*}
donde n! representa la multiplicación de todos los enteros desde 1 hasta n \(n!= n\times (n-1)\times\cdots\times 3\times 2\times 1\), por ejemplo \(4!=4\times 3\times 2\times 1= 24\).
Por supuesto, esta fórmula puede que no sea la más común enseñada en las clases de matemáticas, pero no profundizaremos en eso aquí.
Sin embargo, agregó que esta distribución no tenía en cuenta el orden en que ocurrieron los resultados (el orden no importa).
Para ilustrar su enseñanza, llamó al líder del grupo, el guardabosques, que aceptó lanzar una moneda cinco veces seguidas. Los aventureros, con los ojos fijos en la moneda suspendida, observaron con fascinación mientras la secuencia final revelaba: AASAS.
Con su aura mística, explicó que la probabilidad de obtener precisamente esta secuencia era \(\frac{1}{2^{5}}\),
lo que significaba que había una probabilidad de uno entre 32 de que ocurriera esta secuencia. Los aventureros comenzaban a comprender la importancia de los cálculos de probabilidad en situaciones como esta.
Azar enfatizó que la distribución binomial tenía en cuenta todas las posibles formas de obtener tres Águilas de los cinco lanzamientos (que son 20 posibilidades) y les recordó la fórmula correspondiente.
\begin{equation*}\mathbb{P}(N_1 = 3, N_2=2) =\frac{5!}{3!2!} \cdot p_1^3 \cdot p_2^{2} = 20 \times \frac{1}{2^{5}}\end{equation*}

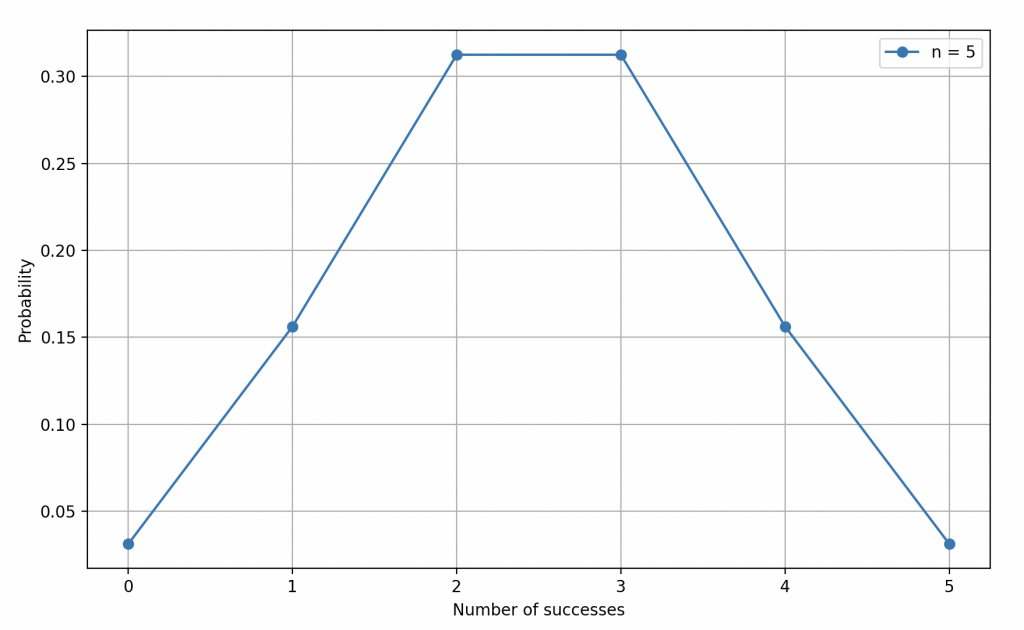
Ley binomial de parámetros \(n=5\) y \(p_1=0.5\).
Luego explicó que la distribución binomial tenía varias características clave esenciales para comprender y analizar un experimento dado.
La esperanza de la distribución binomial, denotada como \(\mathbb{E}(N_1)\), se definió como el valor esperado del número de éxitos en n pruebas, basado en la probabilidad \(p_1\) de éxito en una prueba individual:
\begin{equation*}\mathbb{E}(N_1) = n \cdot p_1 = 0.5\times n\end{equation*}
Azar agregó que la varianza de la distribución binomial se calculaba de la siguiente manera, cuantificando la dispersión de los resultados alrededor de la expectativa y proporcionando información sobre la estabilidad o variabilidad de los resultados:
\begin{equation*}V(N_1) = n \cdot p_1 \cdot p_2 = 0.25\times n\end{equation*}
Luego, Azar ilustró a los aventureros sobre la moda de la distribución binomial, explicando que la moda era el valor de \(n_1\) que maximizaba la probabilidad. Para una moneda equilibrada, enfatizó que la moda se encontraba en \(\frac{n}{2}\), lo que significaba que el resultado más probable era obtener un número igual de Águilas y Soles.
También mencionó la asimetría y la curtosis de la distribución binomial, reconociendo que los cálculos podían ser más complejos que los anteriores.
La asimetría, denotada como \(\gamma_1(N_1)\), se definió como una medida de la asimetría de la distribución binomial, con la siguiente fórmula:
\begin{equation*}\gamma_1(N_1) = \frac{p_2-p_1}{\sqrt{np_1p_2}}=0\end{equation*}
Claramente, cuando la moneda está equilibrada, obtenemos una curva simétrica con respecto al valor medio.
En cuanto a la curtosis, representada por \(\gamma_2(N_1)\), evaluó la forma de la distribución en comparación con una distribución normal estándar (una curva en forma de campana), con la siguiente fórmula:
\begin{equation*}\gamma_2(N_1) = \frac{1-6p_1p_2}{np_1p_2}\end{equation*}
Una nota importante a considerar es que a medida que el número de pruebas aumenta, la distribución binomial se acerca a una distribución llamada distribución normal (curva en forma de campana). Esto puede ser útil para modelar fenómenos del mundo real porque la distribución normal es una distribución comúnmente observada en la naturaleza (la estudiaremos en detalle en un artículo futuro).
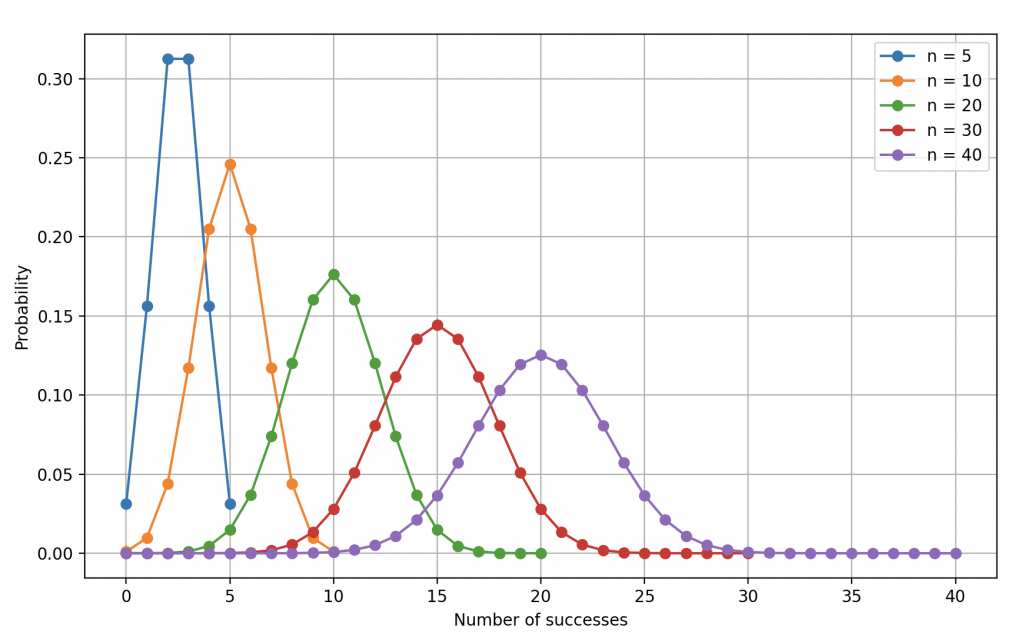
Ley binomial de parámetros \(n=5,10,20,30,40\) y \(p_1=0.5\).

El ser divino concluyó enfatizando que la distribución binomial era una herramienta esencial para modelar experimentos binarios con probabilidades de éxito y fracaso. Características como la media, la varianza, la moda, la asimetría y la curtosis eran todas herramientas para analizar la distribución de resultados posibles, lo que ayudaría a los aventureros a tomar decisiones informadas en sus futuras búsquedas.
La Ley de los Dados
El momento temido se acercaba. Cuatro soldados, firmes defensores de su guarnición, avanzaron para enfrentar a nuestros valientes héroes. Para triunfar sobre estos formidables oponentes, necesitarían aprovechar el poder de sus dados mágicos y hacer buenas tiradas.
Soldado 1: 3 veces el número 6, 1 vez el número 5, 0 veces el número 4, 1 vez el número 3, 1 vez el número 2 y 1 vez el número 1.
Soldado 2: 0 veces el número 6, 1 vez el número 5, 3 veces el número 4, 0 veces el número 3, 1 vez el número 2 y 2 veces el número 1.
Soldado 3: 2 veces el número 6, 1 vez el número 5, 1 vez el número 4, 1 vez el número 3, 1 vez el número 2 y 1 vez el número 1.
Soldado 4: 1 vez el número 6, 1 vez el número 5, 1 vez el número 4, 1 vez el número 3, 3 veces el número 2 y 0 veces el número 1.
Mago: 7 veces el número 6, 0 veces el número 5, 0 veces el número 4, 0 veces el número 3, 0 veces el número 2 y 0 veces el número 1.
En esta situación, la complejidad radicaba en que, en lugar de tener solo dos resultados posibles, como en una simple tirada de moneda, ahora tenían seis resultados posibles, y esto podía variar según las circunstancias, a veces más, a veces menos (según los dados que usen).
Azar: (con una voz tranquilizadora) Para ayudarte a entender mejor, centrémonos en un dado estándar de seis caras. Dado que los dados no están cargados, la probabilidad de sacar un 6, que denotaremos como\(p_6\), es la misma que sacar un 1 (y todos los demás), denotado como \(p_1\)
y ambos son 1/6. Por lo tanto, es como una tirada de moneda justa, donde cada resultado tiene igual probabilidad de ocurrir (la distribución uniforme discreta).
Azar continuó explicando que, por analogía con la distribución binomial, para cualquier dado, la probabilidad de obtener\(n_6\) valores de 6, \(\cdots\), \(n_1\) valores de 1 en n lanzamientos de un dado es:
\begin{equation*}
\mathbb{P}(N_6=n_6, \cdots, N_1=n_1) =\frac{n!}{n_6!n_5!n_4!n_3!n_2!n_1!} \cdot p_1^{n_1} \cdot p_2^{n_2}\cdot p_3^{n_3}\cdot p_4^{n_4}\cdot p_5^{n_5}\cdot p_6^{n_6}
\end{equation*}
y para un dado justo, esto se simplifica a:
\begin{equation*}
\mathbb{P}(N_6=n_6, \cdots, N_1=n_1) =\frac{n!}{n_6!n_5!n_4!n_3!n_2!n_1!} \cdot\left(\frac{1}{6}\right)^n
\end{equation*}
Esta fórmula tenía en cuenta la cantidad de formas de organizar los resultados del dado para cada lanzamiento y las probabilidades de obtener cada cara. En el caso de un dado justo, esta fórmula se simplificaba utilizando la probabilidad de 1/6 para cada cara.
Azar luego aplicó estos conceptos matemáticos para explicar que la probabilidad de derrotar al Soldado 1 era muy baja, calculada en aproximadamente 0.003. Nuestros héroes permanecieron perplejos, dándose cuenta de que sus posibilidades de éxito eran escasas.
\begin{equation*}\mathbb{P}(N_6=3, N_5 = 1, N_4 = 0, N_3 = 1, N_2 = 1, N_1=1)=\frac{7!}{3!1!0!1!1!1!}\cdot\left( \frac{1}{6}\right)^7\approx0,003\end{equation*}
Enfrentando su destino, los aventureros lanzaron los dados, esperando obtener la secuencia mágica. Increíblemente, lograron derrotar al primer soldado al obtener la secuencia 1, 6, 6, 6, 5, 2, 3, una combinación que tenía una probabilidad extremadamente baja de ocurrir, solo 1 entre 279,936, al igual que todas las configuraciones posibles en 7 lanzamientos.
Azar no profundizó mucho en las propiedades de esa distribución, solo las más clásicas, el valor esperado y la varianza, que tienen las mismas formulaciones que para la distribución binomial. Tampoco enseñó sobre su representación gráfica, ya que la humanidad no puede visualizar fácilmente curvas en más de tres dimensiones. Aquí, hay 6! Por lo tanto, solo era necesario adaptarse a la representación de la distribución binomial y usar un poco de imaginación.
Nuestros héroes habían triunfado sobre el primer obstáculo, pero el camino que les esperaba seguía siendo largo e incierto. Ahora habían comprendido la importancia crucial de la probabilidad y la distribución multinomial en su búsqueda. Armados con este conocimiento poderoso, se prepararon para enfrentar a los soldados restantes con determinación inquebrantable y un destello de esperanza en sus ojos. La batalla aún no estaba ganada, pero estaban listos para enfrentar la incertidumbre que les esperaba.
Sin embargo, a pesar de su dominio de las probabilidades, nuestros aventureros no eran invencibles. Su viaje finalmente los llevó al mago, cuyas probabilidades de derrota eran aún más escasas. El destino así lo decretó, y nuestros héroes fueron derrotados por el mago, a pesar de su valentía.
¡Engaño!
Mientras nuestros héroes eran arrastrados por los misterios de su destino, Azar les reveló una profunda verdad: el orden de los acontecimientos no tenía importancia fundamental, a diferencia de la serie de coincidencias improbables que los habían llevado hasta él (les aconsejó calcular la probabilidad de llegar hasta él sin morir). Estas circunstancias fortuitas habían dado forma inesperadamente a su destino, como si el hilo narrativo se hubiera entrelazado con los hilos del azar.
Era como si todo este viaje hubiera sido un juego, un juego que había comenzado cuando el ladrón le había lanzado esa moneda al enano en la taberna. Cada tirada de dados en la celda, cada enfrentamiento contra los soldados, todo había contribuido a esculpir su destino, llevándolos inexorablemente hacia Azar. La realidad y la ficción se habían entrelazado, creando una emocionante aventura donde la probabilidad se había convertido en el hilo conductor.
Nuestros héroes, en una mezcla de diversión y reflexión, recordaron las lecciones de probabilidad, dándose cuenta de cuánto podían influir en el curso de su historia el entender tales conceptos. Saborearon su regreso, conscientes de que incluso en la narrativa de sus vidas, el azar tenía su propio lugar, tejiendo un tapiz complejo y cautivador.
Bibliografía
P. Bogaert, Probabilités pour scientifiques et ingénieurs : Introduction au calcul des probabilités, De Boeck Supérieur, 2005, 402 p
E. Gossett, Discrete Mathematics with Proof, Hoboken (N.J.), John Wiley & Sons, 2009, 904 p
E. Lesigne, Heads or tails : an introduction to limit theorems in probability, Providence (R.I.), AMS, 2005, 150 p.
D. Foata, A. Fuchs et J. Ranchi, Calcul des probabilités : Cours, exercices et problèmes corrigés, Paris/Berlin/Heidelberg etc., Dunod, 2012, 3e éd., 368 p.
import matplotlib.pyplot as plt
import scipy.stats as stats
# Parameters of the binomial distribution
p = 0.5 # Probability of success
n_values = [5, 10, 20, 30, 40] # Different values of n
# Create the graph
plt.figure(figsize=(10, 6))
# Simulation and plotting of curves for each value of n
for n in n_values:
x = range(n + 1)
y = [stats.binom.pmf(k, n, p) for k in x]
plt.plot(x, y, marker='o', label=f'n = {n}')
# Labeling of axes and adding a title
plt.xlabel('Number of successes')
plt.ylabel('Probability')
# Display the legend
plt.legend()
# Display the graph
plt.grid(True)
plt.show()
