El ladrón desliza con precaución su ganzúa en la cerradura, pero el penetrante hedor y la incomodidad perturban su concentración. Siente que la cerradura se resiste, pero no se rinde. Luego, escucha un sonido que no le gusta. Cuando retira su ganzúa, se da cuenta de que la mitad de ella está atascada en la puerta, lo que disminuye sus posibilidades de escape a nada.
El carcelero, en su prisa por ver lo que estaba sucediendo, llega a la puerta y abre el mirador de metal, pero es golpeado de inmediato por un olor insoportable. Se da cuenta demasiado tarde de que ha pisoteado la sustancia nociva que se ha esparcido por la celda. Sorprendido, el carcelero emite un grito de asco y comienza a maldecir a los prisioneros.
Carcelero: (furioso) ¡Por los infiernos, ¿qué es esto?! ¡Banda de inmundos!
A pesar de su incomodidad, el carcelero echa un vistazo dentro de la celda y se da cuenta de que los prisioneros han causado un daño significativo. Intenta abrir la puerta pero se da cuenta de que las llaves no encajan en la cerradura. Han bloqueado la celda. Una sonrisa satisfecha cruza su rostro.
Carcelero: (satisfecho) ¡Por los dioses, han bloqueado la puerta! ¿Cómo demonios lo hicieron? ¡Quédense en su porquería, idiotas!
Los aventureros, aún prisioneros, se encuentran ahora atrapados en su propia inmundicia. La fuga parece imposible, a pesar del persistente hedor de la celda. Sin embargo, la maga continúa su exposición sobre la ley de probabilidad triangular imperturbable, tratando de encontrar sentido en esta situación caótica.
La Ley de Dos Dados
Maga: Mis queridos amigos, ahora que tienen un sólido entendimiento de la distribución uniforme discreta, permítanme hablarles sobre otra distribución intrigante, la distribución triangular, que ocurre cuando lanzamos dos dados de seis caras y sumamos los valores obtenidos en sus caras superiores.
A diferencia de la distribución uniforme de la que hablamos anteriormente, la distribución triangular tiene una distribución de probabilidades diferente.
En un simple lanzamiento de un dado justo de seis caras, la probabilidad de obtener cualquier valor del 1 al 6 se distribuye uniformemente, con 1/6 de probabilidad para cada resultado. Esto constituye una distribución uniforme discreta. Sin embargo, cuando lanzamos dos dados y sumamos los valores, los resultados ya no están uniformemente distribuidos, sino que siguen una distribución triangular.

La suma de los dados puede variar desde 2, cuando ambos dados muestran un 1, hasta 12, cuando ambos dados muestran un 6. Aquí tienes la distribución de probabilidades para la suma de los dados:
Suma de los dados es 2: Probabilidad 1/36
Suma de los dados es 3: Probabilidad 2/36
Suma de los dados es 4: Probabilidad 3/36
Suma de los dados es 5: Probabilidad 4/36
Suma de los dados es 6: Probabilidad 5/36
Suma de los dados es 7: Probabilidad 6/36
Suma de los dados es 8: Probabilidad 5/36
Suma de los dados es 9: Probabilidad 4/36
Suma de los dados es 10: Probabilidad 3/36
Suma de los dados es 11: Probabilidad 2/36
Suma de los dados es 12: Probabilidad 1/36
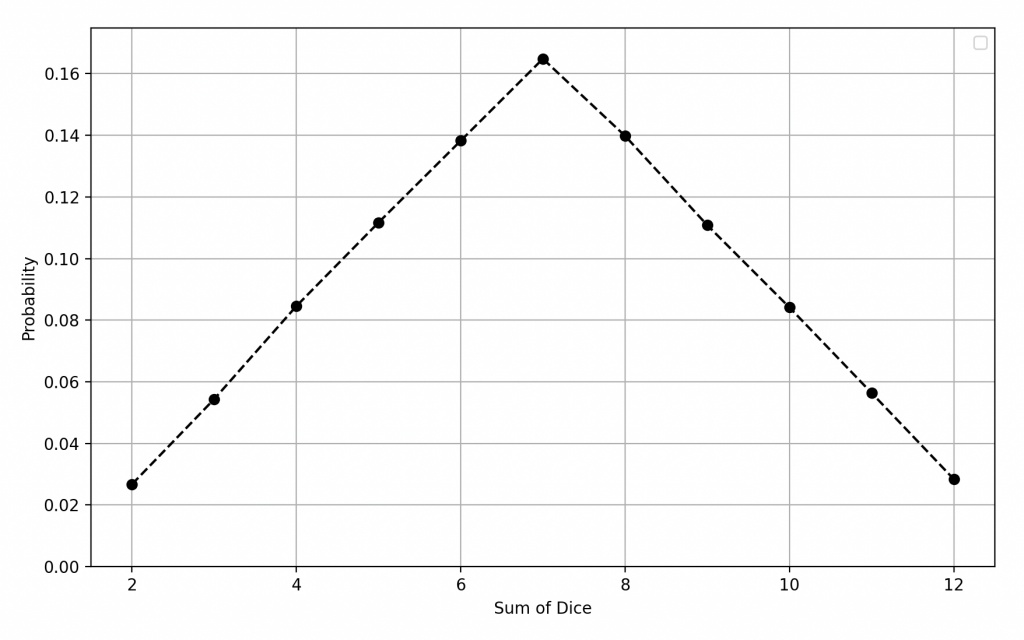
Como puedes ver, la suma más probable es 7, con una probabilidad de 6/36, mientras que los extremos, 2 y 12, tienen la probabilidad más baja, solo 1/36.
Existen varias combinaciones posibles con dos dados de seis caras para obtener una suma específica. Permíteme enumerarlas:
Para obtener una suma de 2, solo hay una combinación posible: 1+1.
Para obtener una suma de 3, hay dos combinaciones posibles: 1+2 y 2+1.
Para obtener una suma de 4, hay tres combinaciones posibles: 1+3, 2+2 y 3+1.
Y así sucesivamente, hasta llegar a una suma de 12, que tiene solo una combinación posible: 6+6.
Esta distribución triangular es fascinante porque refleja cómo se distribuyen las probabilidades al combinar los resultados de dos dados. Ten en cuenta que este conocimiento podría resultarte útil en tus futuras aventuras, ya que te permitirá estimar las posibilidades de éxito en situaciones que involucren tiradas de dados complejas.
¡La Historia no ha Terminado!
Sin embargo, es importante recordar que todo lo narrado hasta ahora no es el verdadero final de la historia, sino más bien una variación de lo que podría haber ocurrido.
En el mundo de los juegos de rol, las posibilidades son infinitas y el destino de nuestros aventureros a menudo depende de las elecciones de los jugadores y las decisiones del Director de Juego. Así que dejemos que la búsqueda continúe, porque cada aventura es única e impredecible, y nuevos desafíos esperan a nuestros valientes héroes en los rincones más oscuros.
Encontremos el verdadero final.
Bibliografía
M. Fréchet, M. Halbwachs, Le calcul des probabilités à la portée de tous, Dunod, 1924, 297 p.
C. Barboianu, Probability Guide to Gambling. The Mathematics of Dice, Slots, Roulette, Baccarat, Blackjack, Poker, Lottery and Sport Bets, INFAROM Publishing, 2006, 316 p
P. Nahin, Digital Dice. Computational Solutions to Practical Probability Problems, Princeton University Press, 2008, 263 p.
I. Stewart, Do Dice Play God?: The Mathematics of Uncertainty, 2019
import matplotlib.pyplot as plt
import numpy as np
# Number of simulations
n_simulations = 100000
# Simulations of rolling two dice and calculating sums
results = np.random.randint(1, 7, size=(n_simulations, 2))
sums = np.sum(results, axis=1)
# Calculation of probability density
unique, counts = np.unique(sums, return_counts=True)
probability = counts / n_simulations
# Creating the probability density plot
plt.figure(figsize=(10, 6))
plt.plot(unique, probability, marker='o', linestyle='--', color='black')
# Labeling axes and adding a title
plt.xlabel('Sum of Dice')
plt.ylabel('Probability')
# Limiting the y-axis scale from 0 to the maximum probability
plt.ylim(0, max(probability) + 0.01)
# Displaying the legend
plt.legend()
# Displaying the plot
plt.grid(True)
plt.show()
