Les dés sont jetés, un silence sourd résonne alors que la boule de billard se dirige vers la fissure dans le mur. Cependant, le destin semble ne pas être de leur côté cette fois-ci. La boule de billard percute le mur et rebondit maladroitement sur le sol de la cellule émettant un léger bruit étouffé. Un silence tendu s’installe parmi les aventuriers, brisé seulement par le léger écho du rebondissement de la boule.
Malgré les appels incessants des aventuriers pour tenter en dernier recours de charmer ou soudoyer le garde, aucun d’entre eux ne se présente. La cellule reste désespérément close, et la magicienne, imperturbable, poursuit son exposé sur la loi de probabilité triangulaire, semblant ignorer la déception de ses compagnons. Les dés, semblent-ils, ont décidé de les garder captifs pour un peu plus longtemps.
La Loi de Deux Dés
Magicienne : Mes chers amis, maintenant que vous avez une solide compréhension de la loi uniforme discrète, laissez-moi vous parler d’une autre distribution intrigante, la loi triangulaire, qui se manifeste lorsque nous lançons deux dés à six faces et que nous additionnons les valeurs obtenues sur leurs faces supérieures.
Contrairement à la distribution uniforme dont nous avons discuté précédemment, la loi triangulaire présente une répartition différente des probabilités.
Pour un simple lancer d’un dé à six faces, équilibré et non pipé, la probabilité d’obtenir n’importe quelle valeur de 1 à 6 est uniformément répartie, soit 1/6 pour chaque résultat. Cela constitue une loi uniforme discrète. Cependant, lorsque nous lançons deux dés et additionnons les valeurs, les tirages ne sont plus uniformément distribués, mais plutôt suivent une distribution triangulaire.

La somme des dés peut varier de 2, lorsque les deux dés affichent 1, à 12, lorsque les deux dés affichent 6. Voici la distribution de probabilité pour la somme des dés :
Somme des dés vaut 2 : Probabilité 1/36
Somme des dés vaut 3 : Probabilité 2/36
Somme des dés vaut 4 : Probabilité 3/36
Somme des dés vaut 5 : Probabilité 4/36
Somme des dés vaut 6 : Probabilité 5/36
Somme des dés vaut 7 : Probabilité 6/36
Somme des dés vaut 8 : Probabilité 5/36
Somme des dés vaut 9 : Probabilité 4/36
Somme des dés vaut 10 : Probabilité 3/36
Somme des dés vaut 11 : Probabilité 2/36
Somme des dés vaut 12 : Probabilité 1/36
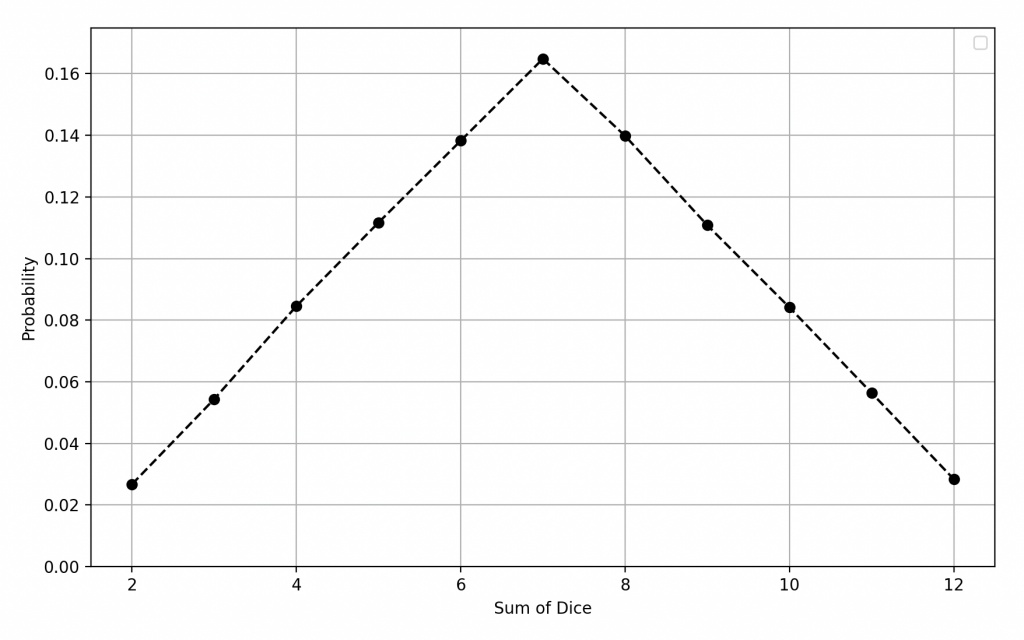
Comme vous pouvez le voir, la somme la plus probable est 7, avec une probabilité de 6/36, tandis que les extrémités, 2 et 12, ont la probabilité la plus faible, avec seulement 1/36.
Il existe plusieurs combinaisons possibles avec deux dés à six faces pour obtenir une certaine somme. Permettez-moi de les énumérer :
Pour obtenir une somme de 2, il n’y a qu’une seule combinaison possible : 1+1.
Pour obtenir une somme de 3, il y a deux combinaisons possibles : 1+2 et 2+1.
Pour obtenir une somme de 4, il y a trois combinaisons possibles : 1+3, 2+2 et 3+1.
Et ainsi de suite, jusqu’à ce que nous atteignions une somme de 12, qui n’a qu’une seule combinaison possible : 6+6.
Cette distribution triangulaire est fascinante car elle reflète la manière dont les probabilités se répartissent lorsque nous combinons les résultats de deux dés. Gardez à l’esprit que ces connaissances pourraient s’avérer utiles dans vos futures aventures, car elles vous permettront d’estimer les chances de succès lorsque vous aurez affaire à des situations où vous devrez faire des tirages de dés complexes.
C'est pas fini!
Cependant, il est important de rappeler que tout ce qui vient d’être raconté n’est pas la vraie fin de l’histoire, mais plutôt une variation de ce qui aurait pu se produire.
Dans le monde du jeu de rôle, les possibilités sont infinies, et le destin de nos aventuriers dépend souvent des choix des joueurs et des décisions du Maître du Jeu. Alors, que la quête continue, car chaque aventure est unique et imprévisible, et de nouveaux défis attendent nos courageux héros dans les recoins obscurs.
Trouvez la vraie fin.
Bibliographie
M. Fréchet, M. Halbwachs, Le calcul des probabilités à la portée de tous, Dunod, 1924, 297 p.
C. Barboianu, Probability Guide to Gambling. The Mathematics of Dice, Slots, Roulette, Baccarat, Blackjack, Poker, Lottery and Sport Bets, INFAROM Publishing, 2006, 316 p
P. Nahin, Digital Dice. Computational Solutions to Practical Probability Problems, Princeton University Press, 2008, 263 p.
I. Stewart, Do Dice Play God?: The Mathematics of Uncertainty, 2019
import matplotlib.pyplot as plt
import numpy as np
# Number of simulations
n_simulations = 100000
# Simulations of rolling two dice and calculating sums
results = np.random.randint(1, 7, size=(n_simulations, 2))
sums = np.sum(results, axis=1)
# Calculation of probability density
unique, counts = np.unique(sums, return_counts=True)
probability = counts / n_simulations
# Creating the probability density plot
plt.figure(figsize=(10, 6))
plt.plot(unique, probability, marker='o', linestyle='--', color='black')
# Labeling axes and adding a title
plt.xlabel('Sum of Dice')
plt.ylabel('Probability')
# Limiting the y-axis scale from 0 to the maximum probability
plt.ylim(0, max(probability) + 0.01)
# Displaying the legend
plt.legend()
# Displaying the plot
plt.grid(True)
plt.show()
