Wall-E: Le Petit Mineur d'Or
Episode II
Par Jordan Moles le 2 Novembre, 2023

Contrairement à ses homologues robotiques du passé, Wall-E se démarquait par sa curiosité insatiable et son désir d’apprendre. Chaque jour, il se perdait dans l’exploration des coins oubliés de la planète, à la quête de trésors enfouis et négligés. Au cours de l’une de ses expéditions, dans une ancienne mine délaissée, Wall-E fit une découverte remarquable : des échantillons d’or étincelants, dissimulés sous des strates de terre et de roche. Intrigué par ces éclats dorés, il se demanda s’il pouvait s’amuser à estimer leur valeur.
En tant que savant robotique, il savait que l’évaluation du prix de ces pépites dépendait de leur pureté. C’est à ce moment précis qu’il entreprit d’explorer un problème d’une simplicité extrême : La Régression Linéaire.
Il est fortement conseillé d'avoir lu l'épisode I avant de continuer !
Dans les Profondeurs du Savoir : la Régression
L’histoire de notre intrépide robot solitaire continue et il se retrouve face à une catégorie fascinante de problèmes : la régression. Ces énigmes le poussent à développer de nouvelles compétences pour estimer des valeurs numériques en fonction de données d’entrée, et elles occupent une place importante dans son vaste répertoire d’explorations.
Wall-E, le petit robot collecteur de déchets, est confronté à des problèmes de régression chaque fois qu’il souhaite prédire une valeur numérique basée sur certaines caractéristiques ou variables continues. Imaginez-le en train d’analyser les données qu’il a recueillies tout en s’efforçant de déterminer le prix d’une pépite d’or en fonction de sa pureté. Dans cette quête, il doit établir une relation mathématique entre les données dont il dispose, telles que la pureté de l’or, et les valeurs qu’il souhaite prédire, à savoir les prix de ces précieuses pépites.
L’une des difficultés auxquelles Wall-E est confronté est de choisir le modèle de régression approprié. Il se demande s’il doit opter pour une régression linéaire simple, ce qui signifie qu’il suppose une relation linéaire entre la pureté de l’or et son prix, ou s’il doit explorer des modèles plus complexes, comme une régression polynomiale. Le choix du modèle est crucial car il affectera la précision de ses prédictions.
Une autre problématique que Wall-E doit résoudre est la manière dont il va évaluer la performance de son modèle. Il ne peut pas se permettre de se tromper dans ses estimations, car une erreur dans l’estimation du prix de l’or pourrait entraîner des conséquences potentiellement désastreuses. Il explore donc diverses mesures d’erreur, telles que l’erreur absolue moyenne et la racine carré de l’erreur quadratique moyenne (pour l’instant c’est du charabia), pour évaluer la précision de ses prédictions.
L’un des défis les plus intrigants auxquels Wall-E est confronté dans les problèmes de régression est l’optimisation des paramètres du modèle. Il doit parcourir un processus itératif d’ajustement de ces paramètres pour minimiser l’erreur entre ses prédictions et les valeurs réelles. Wall-E se lance alors dans la descente de gradient, une technique qui l’aide à trouver les paramètres optimaux en minimisant une fonction coût qui rassemble les erreurs du modèle.
Chaque problème de régression que Wall-E aborde est unique, car les données et les objectifs varient. Cependant, sa persévérance et son ingéniosité, combinées à ses compétences en Machine Learning, lui permettent de relever ces défis et d’estimer avec précision les valeurs numériques, qu’il s’agisse du prix de l’or ou de toute autre tâche de régression.
La Récolte
Peu après l’évasion de l’humanité, le jeune robot senti comme un vent de solitude envahir ses circuits imprimés. Pour s’occuper, après une bonne journée de dur labeur, il parcoure des terrains lointains, fouille dans les décombres des grandes réserves d’or, analyse chacun des alliages précieux, scrute la moindre petite pépite d’or afin d’en déterminer sa pureté et recense tous les échantillons d’or terrestres en les affichant dans un tableau avec leur prix respectifs (voici les 5 premiers échantillons sur les 150).
| Pureté de l'or | Prix de l'or (en boulons) | |
|---|---|---|
| Echantillon 1 | 0.3745 | 1028.1347 |
| Echantillon 2 | 0.9507 | 1456.2091 |
| Echantillon 3 | 0.7320 | 1260.2042 |
| Echantillon 4 | 0.5987 | 1145.5583 |
| Echantillon 5 | 0.1560 | 958.0828 |
Lorsqu’ils sont indiqués, ce tableau constitue une base de donnée d’apprentissage. Chaque échantillon k est donc caractérisé par deux éléments : sa pureté \(x^{(k)}\) qui varie entre 0 (c’est pas de l’or) et 1 (c’est de l’or pur) et son prix \(y^{(k)}\) (celui ci peut aller de 0 à l’infini).
La collecte de ces échantillons représente un moment crucial dans la vie de ce savant robotisé. Voici deux aspects essentiels qu’il doit prendre en considération pour réaliser des estimations précises.
Large éventail de données: Wall-E réalise rapidement que pour obtenir des estimations fiables, il doit disposer d’un grand nombre d’échantillons dans sa base de données.
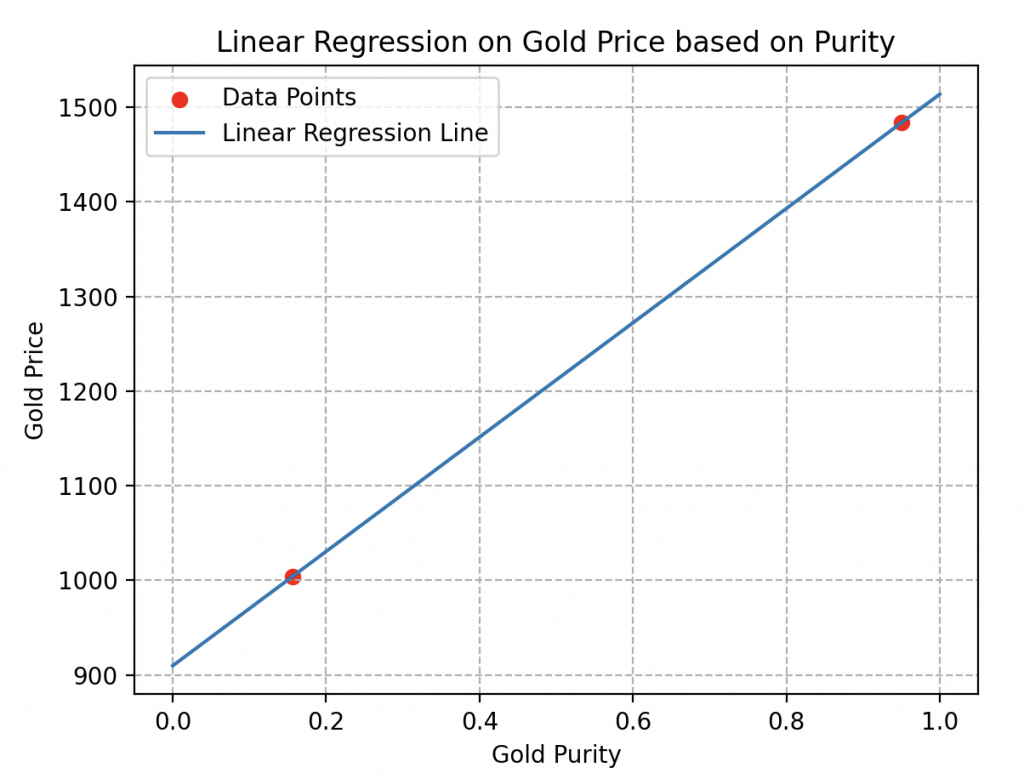
En effet, si l’on considère seulement deux échantillons, comme illustré ici, il est impossible de déterminer si le comportement des prix est linéaire ou non.
De nombreuses courbes d’estimation pourraient passer par ces deux points sans refléter la réalité. Comme les deux courbes ci-dessous par exemple.



Diversité des données: un autre détail crucial à prendre en compte lors de la récolte est la variété des données.
Supposons que Wall-E ne prenne en compte que des échantillons purs ou des échantillons ayant une pureté extrêmement proche (voir la figure ci-contre).
Dans cette situation, tous les échantillons auront presque le même prix, ce qui l’empêcherait d’estimer le prix d’autres alliages d’or.

Conclusion de la collecte: il est donc impératif de rassembler une multitude d’échantillons choisis au hasard pour éviter ces limitations et pour s’assurer d’obtenir des estimations précises pour un large éventail d’alliages d’or.
Création du Modèle Linéaire
À partir de ces données, Wall-E élabore ce que nous avons nommé un modèle linéaire \(f(x)=ax+b\) ou a et b sont les paramètres du modèle.
Un modèle efficace minimise les écarts entre les prédictions de Wall-E \(f(x)\) et les valeurs réelles y des échantillons. Telle une sorte de chercheur d’or moderne, Wall-E ajuste ces paramètres pour aligner au mieux ses estimations avec la réalité, créant ainsi une équation qui lie subtilement pureté et valeur de l’or. Voici sa tentative initiale, qui n’est pas incroyable du tout.


Mesurer les Trésors d'Or : La Fonction Coût
L’étape suivante dans l’apprentissage de Wall-E consiste à évaluer la performance de ce modèle, c’est-à-dire à mesurer les erreurs entre ses prédictions et les valeurs du jeu de données.
Pour le petit robot, la procédure est simple : chaque estimation, notée k, dans le Dataset est confrontée à la réalité. En fonction de l’approche choisie, le programme de Wall-E retourne l’erreur correspondante à chaque prédiction que nous noterons \(err(k)\).
Chacune des estimations de Wall-E est ainsi associée à sa propre marge d’erreur. Au fil des itérations, ces erreurs s’accumulent en nombre jusqu’à atteindre le nombre total d’exemples n dans le Dataset.
On rassemble donc l’ensemble de ces erreurs dans une fonction que l’on appelle fonction Coût, notée \(Γ(a, b)\). C’est une fonction dépendant des paramètres à ajuster et qui calcule simplement la moyenne de toutes les erreurs. Elle s’écrit donc de la manière suivante:
\begin{align*}\Gamma(a, b) &=\frac{err(1)+err(2)+\cdots+err(n)}{n}=\frac{1}{n}\sum_{k=1}^n err(k)\end{align*}
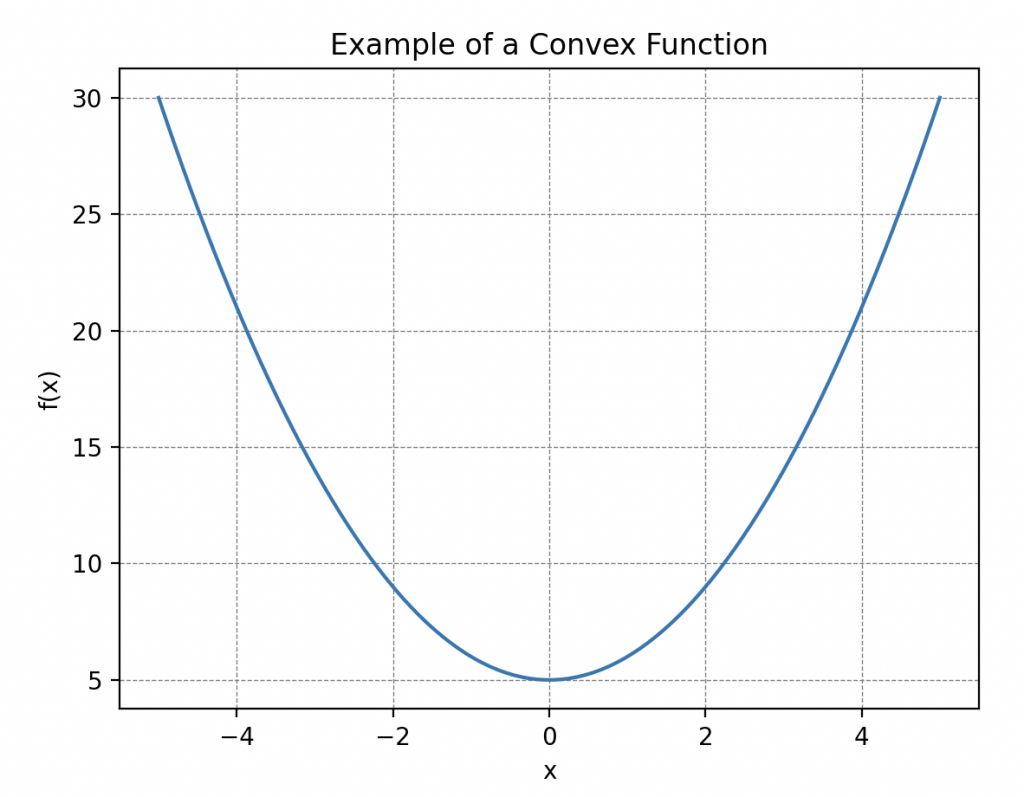
Une propriété importante à prendre en compte sur cette fonction est sa convexité c’est à dire que sa courbe « fait face vers le haut partout », plus précisément, cela signifie que si on trace une droite entre deux points de la courbe alors cette dernière se place toujours au dessus ou au niveau de la courbe. De telles courbes possèdent toujours un minimum global! C’est ce qui va nous servir plus tard.

Les Distances Expliquées par Hal
Wall-E, en plein moment de réflexion, cherchait à comprendre pourquoi il devait prêter attention à la notion de distance. La perplexité l’envahissait alors qu’il observait Hal, son fidèle compagnon cafard, se faufiler silencieusement entre les recoins du laboratoire.
Que pouvait bien signifier cette exploration minutieuse et méthodique de l’espace par Hal ?

Il était bien loin d’imaginer que derrière ces mouvements silencieux et discrets, Hal partageait, à sa manière, les subtilités des distances. Chaque déplacement entre les objets de la pièce illustrait une règle mathématique essentielle. Elle se comptait au nombre de quatre.
La Positivité. Dans cette chorégraphie, Hal démontrait la première: la positivité des distances. Expliquant à sa manière que la distance entre sa cachette préférée et le garde-manger de déchets était toujours positive, un fait simplement illustré par sa trajectoire (une longueur n’est pas négative).
Wall-E, en bon scientifique, l’exprima en termes mathématiques: La distance entre deux points A et B quelconques doit être positive ou nulle. Cela s’écrit,
\begin{align*}
\forall A, B \in E, \quad d(A,B)\geq 0.
\end{align*}
Ce signe \(« \forall »\) veut dire « pour tout » et \(« \in »\) veut dire « dans ». Cela se lit, pour tous éléments quelconques A et B (ici on parle de points) dans E la distance entre A et B est positive ou nulle.
La Symétrie. Le concept de symétrie était ensuite mis en avant par Hal, démontrant comment ses déplacements d’un point A à un point B étaient toujours identiques, qu’il aille de B à A ou d’A à B. Ses allées et venues subtils marquaient ainsi l’idée de symétrie dans cette danse entre les points.
Le petit robot introduit cette idée dans ces circuits: La distance entre A et B doit être la même que entre B et A. Mathématiquement,
\begin{align*}
\forall A, B \in E, \quad d(A,B)=d(B,A).
\end{align*}
La Séparation. Toutefois, la démonstration la plus surprenante pour Wall-E était celle de la séparation. Hal s’en alla chercher deux graines qu’il disposa à deux endroits différent de la pièce. C’est alors qu’il entama une danse frénétique en laissant une graine fixe et ramenant l’autre vers elle en effectuant une série d’aller-retours rapides pour finir par coller les deux graines ensemble.
De cette manière, il voulu illustrer à Wall-E que si la distance entre ces deux points était nulle alors les deux points coïncident. Une représentation impressionnante et claire de la règle de séparation.
Il comprit la leçon qu’il traduisit dans son langage: Si la distance entre A et B est nulle alors A et B coïncident.
\begin{align*}\forall A, B \in E, \quad d(A,B)=0 ⇒A=B.\end{align*}
Ce signe « ⇒ » veut dire « implique ».
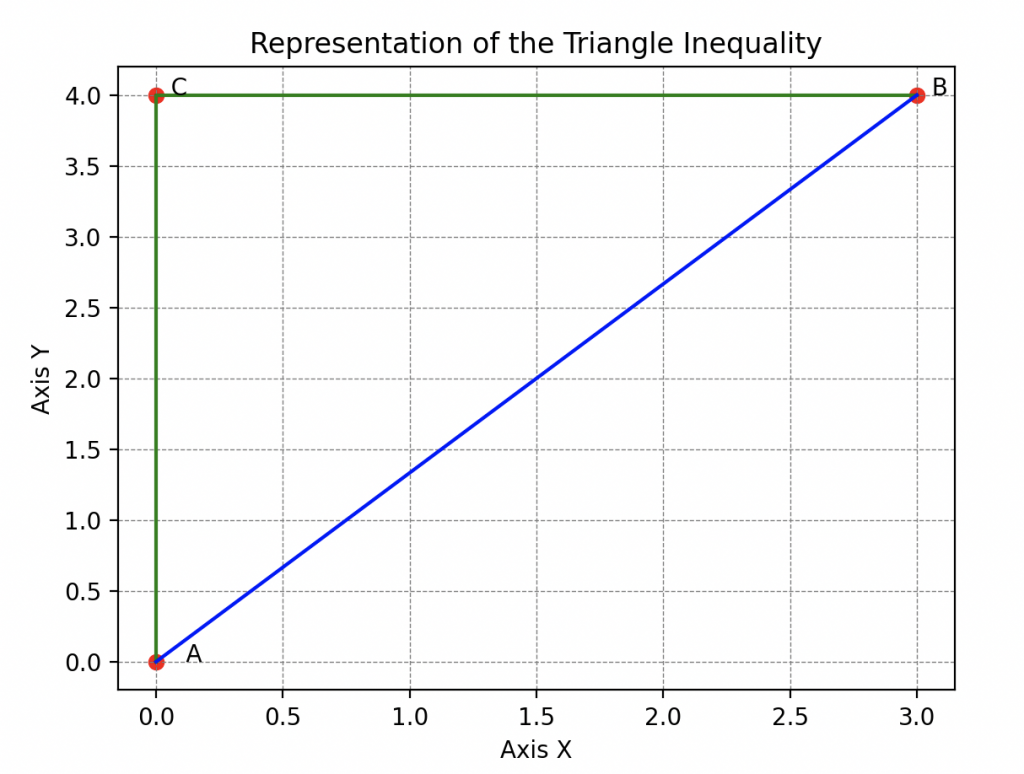
L’Inégalité Triangulaire. Cependant, la leçon de Hal ne s’arrêtait pas là car il restait encore une règle essentielle à analyser. Il continua son exploration en illustrant l’inégalité triangulaire.
En évoluant entre sa cachette, Wall-E et le garde manger Hal montrait que la distance entre sa cachette et Wall-E est toujours inférieure à la distance entre sa cachette et le garde-manger plus la distance entre le garde manger et Wall-E. Cette astuce habile, enseignant que le chemin le plus court entre deux points était la ligne droite, captivait Wall-E.
Il s’empressa donc de retranscrire tout ça: Si je prend trois points A, B et C qui ne coïncident pas alors la distance entre A et B est toujours plus petite ou égale a la distance entre A et C plus la distance entre C et B.
\begin{align*}
\forall A, B, C \in E, \quad d(A,B)\leq d(A,C)+d(C,B).
\end{align*}

Grâce à Hal, Wall-E assimila que formellement, une distance est une fonction qui compare deux points dans un espace donné en y attribuant un nombre réel non négatif, exprimant la « longueur » entre ces deux points et qui suit règles bien précises.
Cet espace peut être le plan familier à deux dimensions comme l’a montré le cafard ou notre espace tridimensionnel, voire des espaces bien plus exotiques.
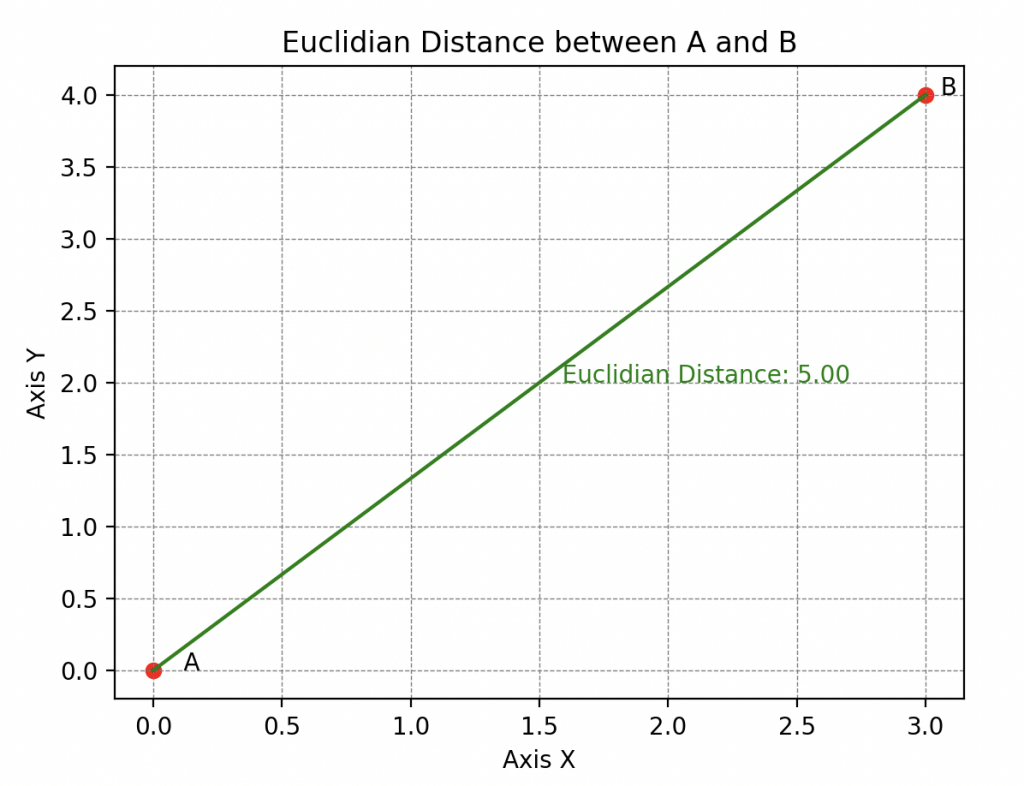
Ses talents d’abstraction lui permettent aussi de comprendre qu’il existe différentes sortes de distances, parmi lesquelles la plus connue est la distance euclidienne (on l’appelle aussi la 2-distance)

ou encore l’\(\infty\)-distance (on dit l’infini-distance) qui évalue la distance maximale entre ces points le long de n’importe quelle dimension.
Mais on trouve également la distance de Manhattan (ou 1-distance pour les puristes) qui est nommée ainsi car elle reflète la distance qu’un taxi devrait parcourir dans un réseau de rues formant des grilles orthogonales (typique de la disposition des rues dans Manhattan, d’où son nom).
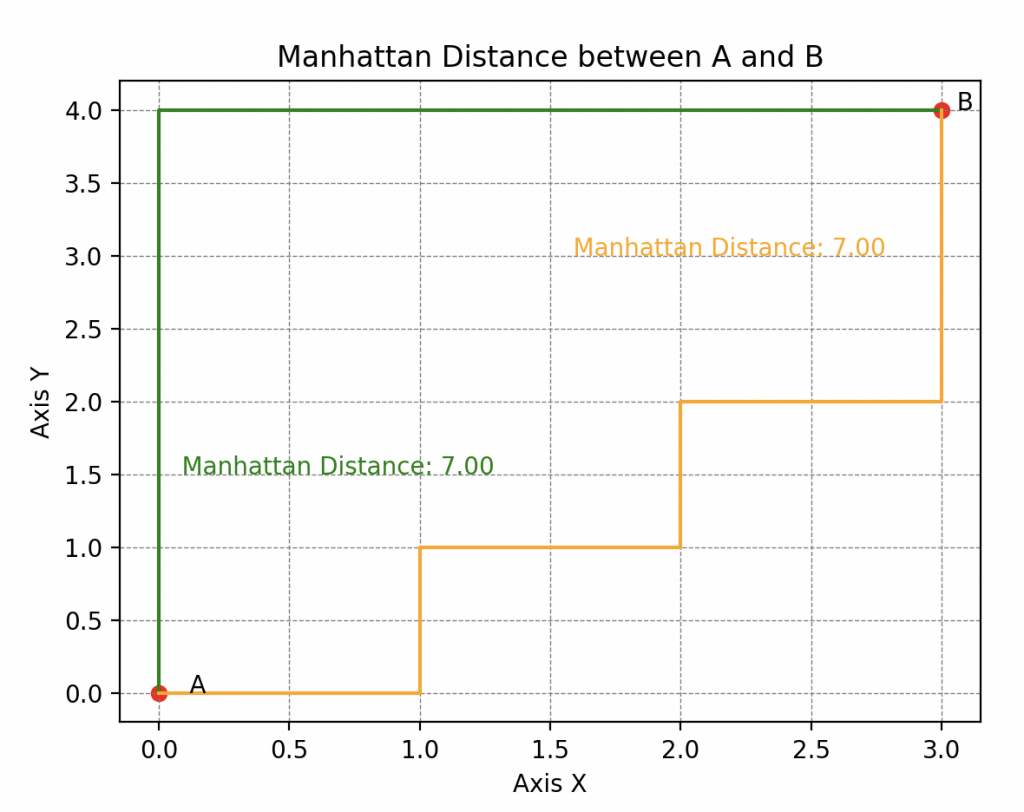
Nous explorerons en détail ces particularités dans un prochain article.
Une Erreur Fatale
Maintenant, pourquoi aborder le concept de distance dans le contexte de l’évaluation des prédictions de Wall-E ? En fait, cela nous amène à réfléchir à ce que sont réellement les erreurs entre les prédictions et les valeurs réelles du Dataset.
Imaginez que Wall-E évalue le premier échantillon, un alliage d’or d’un kilo de pureté 0.72 avec un prix réel de 1231 boulons, mais prédit 1331 boulons. Vous constatez une différence de -130 boulons. Ici on obtient une valeur négative mais en prenant un autre exemple il se pourrait qu’elle soit positive. Cette dualité entre valeurs positives et négatives n’est pas pratique.
Pour résoudre ce problème, deux options s’offrent à nous:
• La première est de considérer la valeur absolue de chaque différence (on enlève le signe moins quand il est présent). L’erreur que l’on obtient se nomme l’erreur absolue notée AE (Absolute Error en anglais).
Dans l’exemple précédent, on aurait \(AE(1) = | 1231–1331| = |-130|=130\).
• La deuxième est de calculer le carré de chaque différence. Cette erreur s’appelle l’erreur quadratique noté SE (Squared Error).
Ici on aurait donc une erreur quadratique \(SE(1)= (1231–1331)^2=(-130)^2=16900\).
On remarque que la deuxième option amplifie grandement les erreurs, mais nous verrons comment rééquilibrer ces différences plus tard.
Ainsi, en appliquant l’une ou l’autre de ces options, on choisit la manière dont on souhaite mesurer les erreurs, c’est à dire une distance. La \(\infty\)-distance pour la première ou la distance euclidienne pour la deuxième.
Maintenant, la procédure est simple : chaque estimation, notée k, dans le Dataset est confrontée à la réalité. En fonction de l’approche choisie, le programme de Wall-E retourne l’erreur correspondante. D’ailleurs, selon la distance choisie, la fonction coût se nomme différemment:
• Si nous considérons l’approche des erreurs absolues, elle se nomme l’erreur absolue moyenne noté MAE (Mean Absolute Error en anglais) et s’écrit \begin{align*} MAE(a, b) &=\frac{AE(1)+AE(2)+\cdots+AE(n)}{n}=\frac{1}{n}\sum_{k=1}^n AE(k)\\ &= \frac{1}{n}\sum_{k=1}^n\left|f\left(x^{(k)}\right) – y^{(k)}\right|=\frac{1}{n} \sum_{k=1}^{n} \left|ax^{(k)} + b- y^{(k)}\right|. \end{align*}
• Tandis que l’approche des erreurs quadratiques, nous fourni une fonction coût que l’on nomme erreur quadratique moyenne noté MSE (Mean Squared Error en anglais) et s’écrit
\begin{align*}
MSE(a, b) &=\frac{SE(1)+SE(2)+\cdots+SE(n)}{n}=\frac{1}{n}\sum_{k=1}^n SE(k)\\
&= \frac{1}{n}\sum_{k=1}^n\left(f\left(x^{(k)}\right) – y^{(k)}\right)^2=\frac{1}{n} \sum_{k=1}^{n} \left(ax^{(k)} + b- y^{(k)}\right)^2.
\end{align*}
Pour remettre à l’échelle initiale nos erreurs calculées par cette fonction là, on prendra juste sa racine carré. La fonction ainsi obtenu se nomme la racine carré de l’erreur quadratique moyenne noté RMSE (Root Mean Squared error).
Voici un exemple pour illustrer le calcul ou Wall-E estime la valeur de seulement cinq échantillons (avec cinq différences).
| Différences | -100 | 7 | -2 | 42 | 13 |
| Erreurs AE | 100 | 7 | 2 | 42 | 13 |
| Erreurs SE | 10 000 | 49 | 4 | 1764 | 169 |
Calcul de la MAE
Calcul de la RMSE
\begin{align*}MAE(a, b) =\frac{100 + 7 + 2 + 42 + 13}{5} = 32.8.\end{align*}
\begin{align*}RMSE(a, b) =\sqrt{\frac{10000 + 49 + 4 + 1764 + 169}{5} }= 48.96.\end{align*}
Pourquoi choisir l’une ou l’autre ? Pour répondre à cette question, introduisons Eve.

| Erreur 1 | Erreur 2 | Erreur 3 | Erreur 4 | MAE | |
|---|---|---|---|---|---|
| Modèle 1 | 20 | 0 | 0 | 0 | 5 |
| Modèle 2 | 6 | 5 | 6 | 4 | 5.25 |
| Erreur 1 | Erreur 2 | Erreur 3 | Erreur 4 | RMSE | |
|---|---|---|---|---|---|
| Modèle 1 | 20 | 0 | 0 | 0 | 10 |
| Modèle 2 | 6 | 5 | 6 | 4 | 5.31 |
Ici on observe que la MAE du modèle 1 est plus petite que celle du modèle 2 donc Eve choisira le modèle 1 pour estimer ces tirs.
Sauf que dans le premier modèle on observe qu’Eve ne fait quasiment aucunes erreurs sauf sur son premier tir ou elle se trompe de 20 cm. Une quantité non négligeable et dangereuse car elle pourrait blesser quelqu’un si son arsenal n’est pas suffisamment précis.
Dans ce tableau, c’est complètement différent, on observe que la RMSE du modèle 1 est beaucoup plus mauvaise que le modèle 2 puisqu’elle affiche une erreur beaucoup plus grande.
Eve aura donc tendance à choisir le modèle 2 dans ce cas. En fait, la RMSE pénalise beaucoup plus les grandes erreurs que la MAE.
Si Eve privilégie la Mean Absolute Error (MAE), cela signifie qu’elle souhaite minimiser les écarts absolus entre l’impact de son tir et la cible. Cela suggère que pour Eve, chaque écart a la même importance. Un écart de 20 unités est considéré comme vingts fois plus important qu’un écart de 1 unités.
En revanche, si Eve choisit de privilégier la Root Mean Squared Error (RMSE), cela signifie qu’elle veut mettre l’accent sur les gros écarts. Dans ce cas, les erreurs plus importantes ont un poids plus significatif. En effet, un écart de 20 unités est 400 fois plus important qu’un écart d’une unité. Donc, si Eve veut éliminer les tirs avec de très gros écarts, le modèle basé sur RMSE serait plus adapté.
Ces choix de fonctions de coût dépendent des objectifs d’Eve : si elle veut réduire les gros écarts, elle privilégiera le MSE. En revanche, si elle veut une évaluation équilibrée de tous les écarts, elle optera pour le MAE. Aussi, il existe d’autres manières de mesurer les erreurs mais nous n’en parlerons pas ici.
Un Petit Pas Pour le Robot, un Grand Pas pour l'Algorithme
Ce qui plaît le plus à Wall-E c’est d’apprendre par lui-même quels sont les paramètres qui minimise la fonction coût, c’est-à-dire les paramètres qui nous offrent le meilleur modèle possible. Pour trouver ces paramètres optimaux, Wall-E utilise un algorithme d’optimisation bien connu appelé descente de gradient. Imaginez cette étape comme si Wall-E ajustait minutieusement les boutons de son modèle mathématique pour atteindre le niveau d’expertise nécessaire dans la tâche de prédiction du prix de l’or en fonction de sa pureté.
On Descend !
L’idée de la descente de gradient est simple : visualisez Wall-E perdu sur les flanc d’une montagne de déchets dans un brouillard épais en train de recycler ce qui lui reste à faire. Malheureusement pour lui, ses piles commencent à s’atténuer dangereusement et doit donc rejoindre son petit vaisseau qui se trouve au point le plus bas, mais il ne peut voir que les pentes immédiates autour de lui. Ainsi, a chaque pas de longueur \(\delta\) (c’est la lettre delta en grec) il choisit la direction qui le fait descendre le plus rapidement possible. Au fur et à mesure qu’il avance, il ajuste sa direction en fonction des pentes qu’il perçoit, se rapprochant progressivement du point le plus bas.
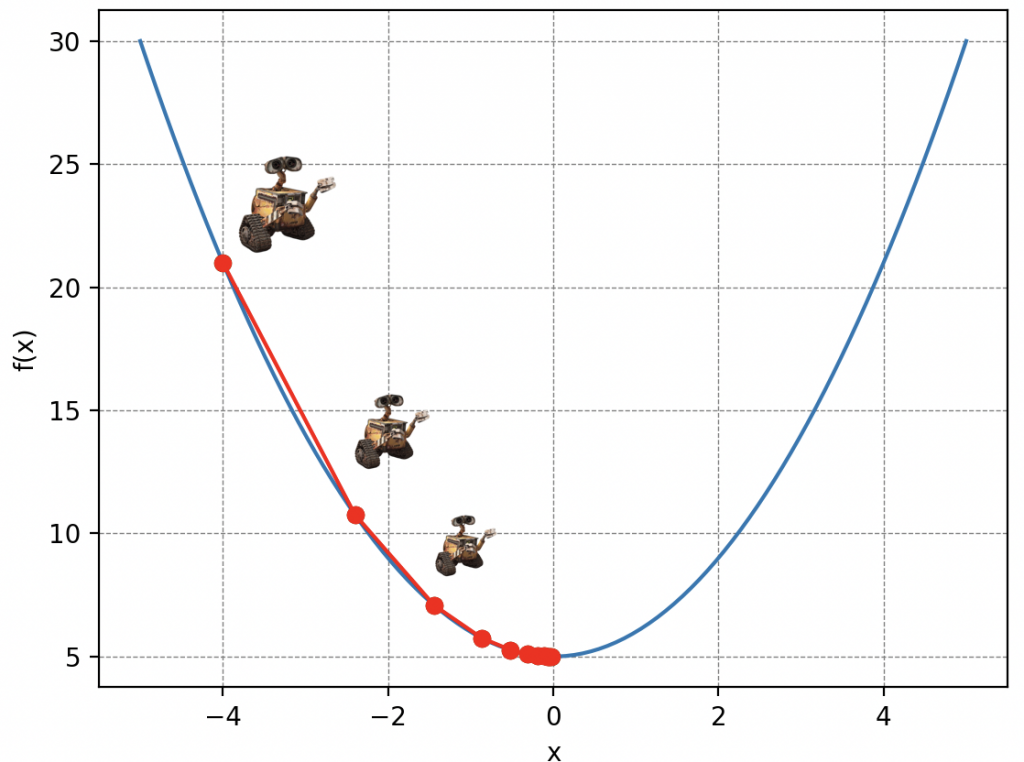

Evidemment, le choix de la valeur \(\delta\) est crucial dans la descente de gradient. Car imaginez que Wall-E se déplace avec des pas trop petits alors il arrivera en bas dans beaucoup trop longtemps, ou qu’il utilise son jetpack pour s’envoler sur des distances très grandes alors il risque de passer au dessus de son refuge.

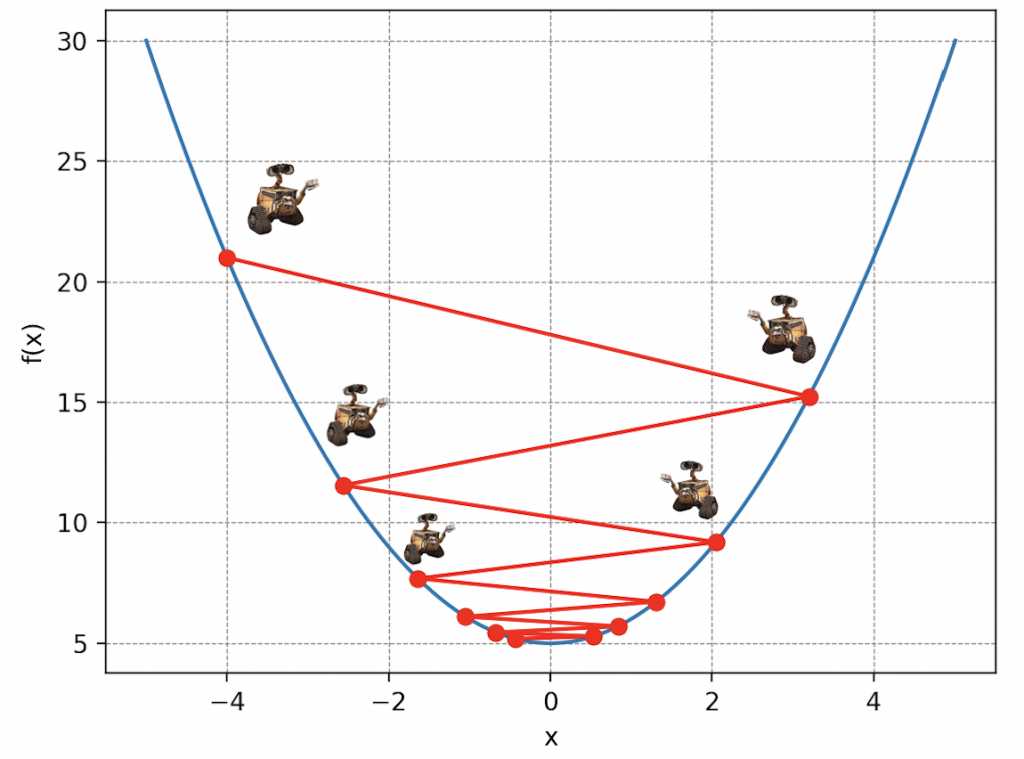
Revenons à notre problème initial. La montagne de déchets symbolise notre fonction coût, les paramètres de position de Wall-E sur la montagne représentent les paramètres de notre modèle de régression linéaire et les pas traduisent ce que l’on appelle le taux d’apprentissage de Wall-E (Learning Rate en anglais). Ainsi, en décomposant les actions de Wall-E, algorithmiquement, on a:
• Notre robot calcule les gradients c’est à dire l’inclinaison de la pente suivant les deux axes (a et b) de la fonction coût à chaque itération. Cela revient mathématiquement à calculer ces deux quantités:
\begin{align*} \frac{\partial \Gamma(a, b)}{\partial a}\quad\text{et}\quad \frac{\partial \Gamma(a, b)}{\partial b} \end{align*} Les mathématiciens l’auront bien compris, ça n’est autre qu’un calcul de dérivée d’une fonction à plusieurs variables.
• Il met à jour les paramètres ce qui le rapproche de plus en plus du minimum de la fonction coût. On appelle les nouveaux paramètres \(a^*\) et \(b^*\) et ils s’écrivent \begin{align*} a^*&=a-\delta\times\frac{\partial \Gamma(a, b)}{\partial a}\\ b^*&=b- \delta\times\frac{\partial \Gamma(a, b)}{\partial b} \end{align*} Ainsi, les nouveaux paramètres sont juste définis comme l’ancienne position auquel on retranche le taux d’apprentissage \(\delta\) multiplié par la valeur de la pente. Par analogie, c’est la position de Wall-E après avoir fait un pas dans la direction ou la pente est la plus forte.
• Il recommence jusqu’à trouver le minimum de la fonction coût.
Il faut bien comprendre que la descente de gradient est un processus itératif c’est à dire qui se répète de nombreuses fois jusqu’à ce que Wall-E atteigne un point où la fonction coût est minimale et ses prédictions sont aussi précises que possible.
En ce qui concerne le taux d’apprentissage noté \(\delta\), quelques détails méritent d’être éclaircis. Comme dans la métaphore précédente, le choix de la valeur de \(\delta\) est essentiel.
Un \(\delta\) trop petit pourrait ralentir la convergence, car les ajustements aux paramètres seraient minuscules à chaque étape, tandis qu’un \(\delta\) trop grand pourrait provoquer des oscillations ou même empêcher la convergence, car les ajustements pourraient dépasser le minimum recherché. Choisir judicieusement la valeur de \(\delta\) est donc essentiel pour que l’algorithme de Wall-E converge efficacement vers la solution optimale.
Quand Est-ce qu'On Arrive ?
Ça fait un petit moment maintenant que notre robot courageux avance désespérément à tâtons, aveuglé par mère nature. Il se demande bien quand est-ce qu’il va arriver en bas de la montagne. Tout comme dans cette situation, en machine learning, atteindre le minimum de la fonction coût – l’équivalent du refuge pour Wall-E – peut sembler délicat. Sa position est incertaine, et pour y arriver, Wall-E doit ajuster sa progression en tenant compte de la longueur de ses pas et du nombre de ces pas.
Pour s’orienter, Wall-E doit donc enregistrer scrupuleusement chacune de ses positions le long du flanc de la montagne que l’on nomme l’histoire de la descente. En gardant une trace précise de chaque pas, il peut ensuite dessiner sa trajectoire, créant ainsi une « courbe de descente ». Cela lui permet de visualiser son chemin parcouru, de mesurer ses progrès et de déterminer s’il est proche du point le plus bas. Voici un exemple ci-dessous, en supposant que Wall-E soit placé au hasard sur la montagne.


Dans le domaine du Machine Learning, l’histoire de la descente se nomme en fait l’histoire du coût car elle donne les valeurs de la fonction coût en fonction de variables clés telles que le taux d’apprentissage et le nombre d’itérations de l’algorithme de la descente de gradient.
D’ailleurs sa représentation graphique que l’on a nommée courbe de descente se nomme en réalité courbe d’apprentissage et est essentielle pour évaluer la performance d’un modèle car elle illustre de façon dynamique l’évolution de la précision du modèle.
Dans ce cas particulier, après une dizaine d’étapes, Wall-E semble cesser de descendre davantage, indiquant qu’il a atteint son refuge. Les 40 pas supplémentaires sont donc inutiles. Cette information est cruciale en informatique, car elle nous permet d’éviter d’exécuter inutilement l’algorithme, potentiellement économisant du temps et des ressources, surtout lorsque certaines simulations peuvent prendre des délais considérables, allant de jours à des semaines.
Dans ses Circuits Imprimés: l'Estimation du Prix de l'Or
Mais que ce passe t’il exactement dans le cerveau électronique de notre adorable robot ? Avant d’effectuer la moindre addition, Wall-E traduit non pas seulement l’ensemble des données sous forme de tableau mais aussi les paramètres du modèle et les gradients: Une sorte de langage crypté pour les machines que l’on appelle forme matricielle qui simplifie grandement les calculs. Plus précisément, Cela donne naissance à un vecteur \(\mathbf{Y}\) composé de n éléments correspondant au prix des n échantillons d’or,
accompagné d’une matrice \(\mathbf{X}\) de n lignes et \(m+1\) colonnes qui englobe avec précision chaque feature m (ici il s’agit seulement de la pureté donc il y en a qu’une seule \(m=1\)) et une colonne contenant que des 1 qu’on appellera « biais »
Cette dernière nous permet simplement d’effectuer les calculs matricielles nécessaires à l’apprentissage. À noter que de manière générale on a
En parallèle, un vecteur « paramètre » \(\mathbf{P}\) (une colonne) fait son entrée, regroupant soigneusement tous les paramètres de notre modèle soient a et b
N’oubliez pas que l’on cherche \(\mathbf{P}\) tel qu’il minimise la fonction coût. Grâce à cela, Wall-E peut exprimer toutes les étapes d’apprentissage facilement et estimer le prix d’une pépite d’or au prix inconnu:
• La Récolte s’effectue en affichant les données dans une matrice : chaque échantillon, avec ses caractéristiques de pureté et de prix, trouve sa place dans cette matrice.
• La Création du Modèle est le processus où Wall-E définit les paramètres affichés dans la colonne \(\mathbf{P}\) prise au hasard qui servent à établir la relation linéaire entre la pureté et le prix de l’or \(\mathbf{F(\mathbf{X})}=\mathbf{X\times P}\).
• La Fonction Coût est redéfinie de la manière suivante: \begin{align*} \Gamma(\mathbf{P})=\frac{1}{n}\left(\mathbf{F(X)-y}\right)\cdot\left(\mathbf{F(X)-y}\right) \end{align*} ou le \(\cdot\) est le produit scalaire.
• Trouver le minimum revient à calculer le gradient:
\begin{align*}\frac{\partial }{\partial \mathbf{P}} \Gamma(\mathbf{P})=\frac{1}{n}\mathbf{X\cdot\left(F(X)-y\right)}\end{align*}
et à appliquer itérativement la descente de gradient pour mettre à jour le paramètre P:
\begin{align*}\mathbf{P^*}=\mathbf{P}-\delta \frac{\partial }{\partial \mathbf{P}}\Gamma(\mathbf{P})\end{align*}
ou \(\mathbf{P^*}\) est le nouveau paramètre.
Wall-E, en appliquant minutieusement toutes les étapes, est maintenant prêt à estimer le prix de l’or selon la pureté que vous lui fournissez ! Voici la courbe finale qu’il obtient.
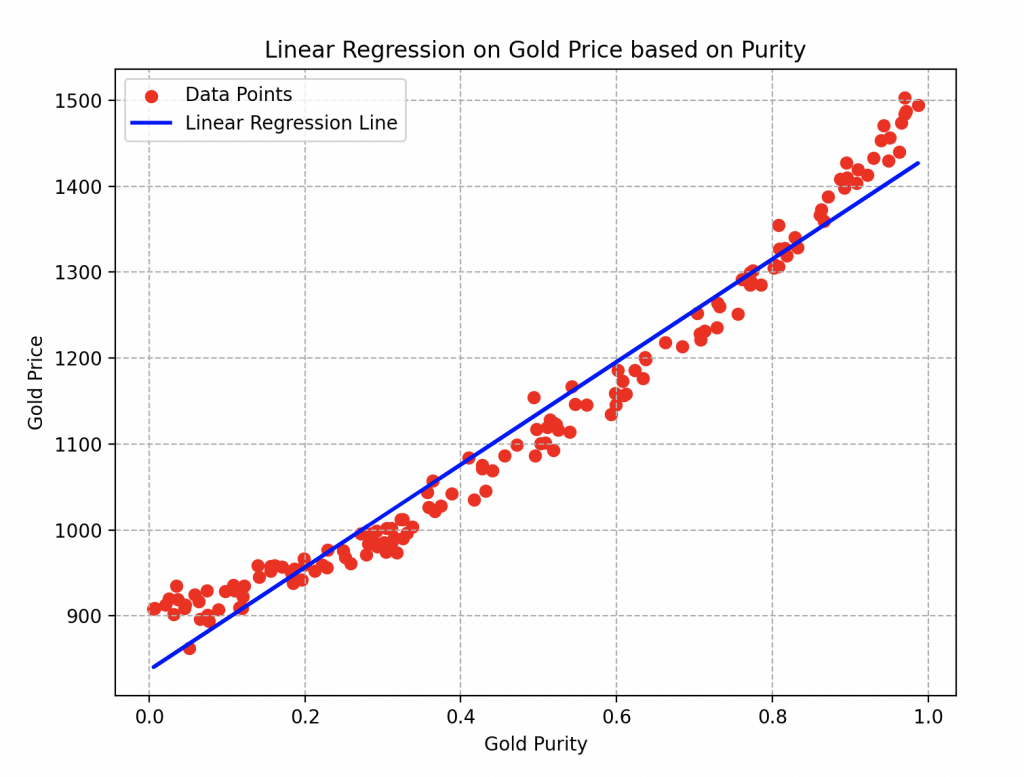
Les paramètres a et b de la droite en bleu sont respectivement égaux à 493.56 et 886.18. Pour la descente de gradient, il a d’ailleurs utilisé un taux d’apprentissage égal à 0.2 et effectué une vingtaine d’itération de l’algorithme.
On peut donc facilement observer qu’en choisissant un alliage d’or de pureté 0.6, son prix serait estimé à environs 1200 boulons.
Transfert de Connaissances et Performance du Modèle : Des Leçons Applicables à Toutes les Régressions
Toutes les étapes et les calculs effectués pour estimer le prix de l’or en fonction de sa pureté via une régression linéaire sont fondamentalement similaires à celles réalisées pour la régression non linéaire ou d’autres types de modèles de Machine Learning !
Wall-E, le petit robot passionné par l’estimation du prix de l’or, accomplit une séquence bien définie pour entraîner son modèle, minimiser l’erreur, et ajuster les paramètres pour prédire le prix de l’or en fonction de sa pureté. Le processus implique la transformation des données en matrices, la création du modèle, la définition de la fonction de coût pour évaluer les erreurs, la minimisation de cette fonction en ajustant itérativement les paramètres, et enfin, l’obtention du paramètre optimal pour estimer avec précision le prix de l’or.
Ce processus est flexible et peut être appliqué à différentes situations et types de modèles d’apprentissage, s’adaptant ainsi à des problèmes plus complexes nécessitant des modèles plus sophistiqués. Le succès de Wall-E dans l’estimation du prix de l’or montre la puissance et l’efficacité de ces méthodes, ouvrant la voie à des applications plus vastes et diversifiées du Machine Learning dans des contextes variés.
Mais il reste encore une dernière chose à voir: Le Coefficient de Détermination aussi connu sous le nom de \(R^2\). Il joue un rôle crucial dans l’évaluation de la performance du modèle de Wall-E car il mesure à quel point le modèle s’ajuste aux données par rapport aux variations de celle-ci. En des termes mathématiques, il s’écrit de la façon suivante:
\begin{equation}R^2 = 1 – \frac{\sum_{k=1}^{n} \left(y^{(k)}- f(x^{(k)})\right)^2}{\sum_{k=1}^{n} (y^{(k)}- \bar{y})^2}\end{equation}
ou \(\bar{y}\) n’est autre que la moyenne des valeurs de nos échantillons (dans notre cas c’est simplement le prix moyen). Sous ses airs barbares, se cache simplement une fraction simple à comprendre. En la réécrivant de manière plus digeste on a,
\begin{equation}R^2 = 1 – \frac{Erreurs}{Variance}.\end{equation}
Souvenez-vous (voir l’article Battre le Maître du Jeu) que la variance est une mesure de la dispersion des valeurs d’échantillons.
Ainsi, pour Wall-E, obtenir un \(R^2\) proche de 1 serait idéal, impliquant que la fraction de droite est proche de 0. Cela signifie que les erreurs sont largement négligeables face à la manière dont se disperse les données et que le modèle proposé par Wall-E s’ajuste bien aux valeurs des échantillons.
A contrario, si \(R^2\) est proche de 0, cela indiquerait que le modèle n’explique pas bien la variabilité des données, et les prédictions peuvent être moins fiables car les erreurs sont du même ordre de grandeur que la variance.
Avec toutes ces explications, Wall-E s’est lancé dans le calcul du coefficient de détermination \(R^2\) pour évaluer la qualité de son modèle précédent. Le résultat est plutôt réjouissant, avec un score honorable de 0,93. En d’autres termes, le modèle s’ajuste remarquablement bien aux données, couvrant environ 93% de la variabilité observée. Une performance qui confirme l’efficacité de son approche dans l’estimation du prix de l’or en fonction de sa pureté !

Cependant, Wall-E, en tant que perfectionniste inlassable, ne se contente pas de succès déjà obtenus. Il cherche constamment des moyens d’améliorer son modèle.
Ainsi, il décide de transcender le modèle linéaire initial en optant pour une approche polynomiale (de degré 2). Il modifie la fonction de référence en \(f(x))=ax^2+bx+c\) et répète méticuleusement toutes les étapes de l’algorithme, ne laissant rien au hasard. Voici les résultats qu’il a obtenus.
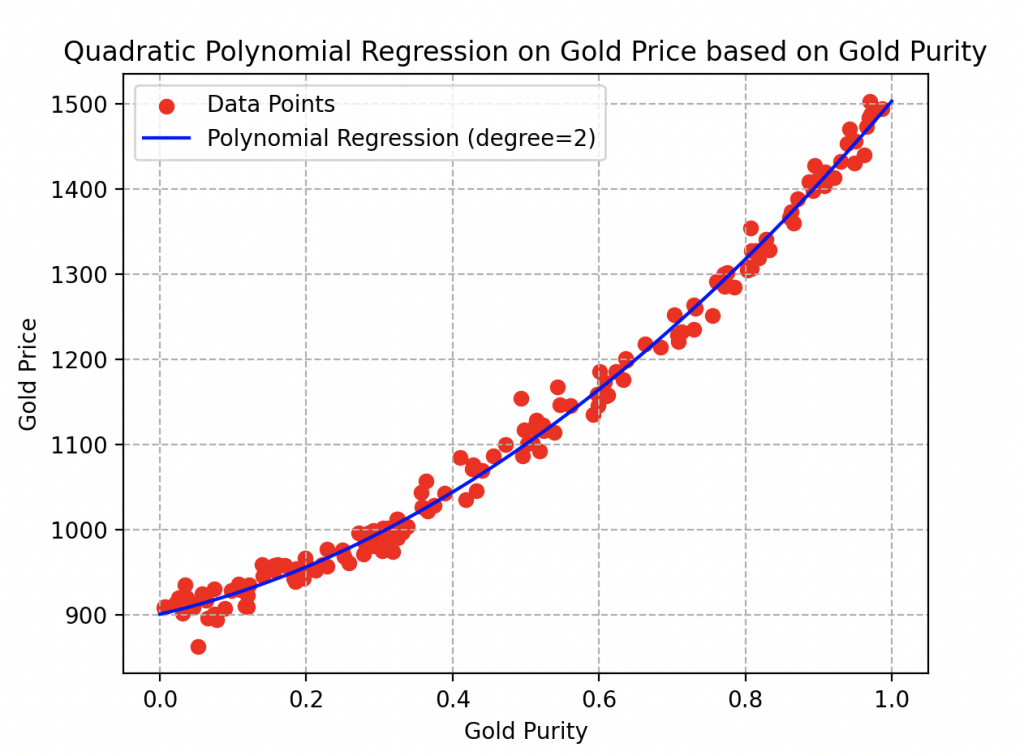
La courbe s’ajuste vraiment bien aux données et pour cause, avec des paramètres valant respectivement 273.84, 404.43 et 837.08, il obtient un coefficient de détermination remarquable de 97 % !
Observez ici qu’un échantillon d’or de pureté 0.6 vaudrait environ 1160 boulons.
En contemplant cette réussite, on ne peut s’empêcher d’anticiper avec enthousiasme les futures explorations de Wall-E dans le monde complexe de la modélisation et de l’apprentissage automatique.
Exploration Réussie des Méandres de la Régression : Prochaine Étape, le Fascinant Monde de la Classification
Dans cette exploration captivante des problèmes de régression, nous avons plongé dans l’univers fascinant de la modélisation mathématique, avec Wall-E comme guide intrépide. Des descentes de gradient aux courbes d’apprentissage, en passant par la définition des erreurs, nous avons démystifié les aspects clés de la régression, révélant la magie sous-jacente du Machine Learning.
Alors que nous laissons Wall-E reposer ses circuits après ses exploits de régression, préparez-vous à embarquer pour une nouvelle aventure dans notre prochain article. Nous plongerons dans les mystères des problèmes de classification, explorant comment les modèles peuvent apprendre à catégoriser et à prendre des décisions dans un monde de données complexes. Restez connectés pour une immersion encore plus profonde dans l’univers dynamique de l’apprentissage automatique avec Wall-E comme votre fidèle compagnon de voyage !
Bibliographie
G. James, D. Witten, T. Hastie et R. Tibshirani, An Introduction to Statistical Learning, Springer Verlag, coll. « Springer Texts in Statistics », 2013
D. MacKay, Information Theory, Inference, and Learning Algorithms, Cambridge University Press, 2003
T. Mitchell, Machine Learning, 1997
F. Galton, Kinship and Correlation (reprinted 1989), Statistical Science, Institute of Mathematical Statistics, vol. 4, no 2, 1989, p. 80–86
C. Bishop, Pattern Recognition And Machine Learning, Springer, 2006
G. Saint-Cirgue, Machine Learnia, Youtube Channel
D.V. Lindley, Regression and correlation analysis, 1987
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression
# Parameters of the quadratic function
a = 400
b = 200
c = 900
# Generate 150 points between -100 and 100
np.random.seed(42)
X = np.random.uniform(0, 1, 150)
# Create Y values based on the quadratic function with Gaussian noise
Y = a * X**2 + b * X + c + np.random.normal(0, 15, 150)
# Reshape the data for modeling
X = X.reshape(-1, 1)
Y = Y.reshape(-1, 1)
# Perform linear regression
model = LinearRegression()
model.fit(X, Y)
# Display the data
plt.figure(figsize=(8, 6))
plt.scatter(X, Y, color='red',label='Data Points')
plt.plot(X, 500 * X + c, color='blue', linewidth=2, label='Linear Regression Line')
#plt.plot(X, model.predict(X), color='blue', linewidth=2, label='Linear Regression Line')
plt.title('Linear Regression on Gold Price based on Purity')
plt.xlabel('Gold Purity')
plt.ylabel('Gold Price')
plt.legend()
plt.grid(ls='--')
plt.show()
import numpy as np
import matplotlib.pyplot as plt
# Parameters of the quadratic function
a = 400
b = 200
c = 900
# Generate random data
np.random.seed(42)
x = np.random.uniform(0, 1, 150)
y = a * x**2 + b * x + c + np.random.normal(0, 15, 150)
y = y.reshape(y.shape[0], 1) # Reshaping y to fit the required shape
# Create the feature matrix X
X = np.vstack((x, np.ones(len(x)))).T
# Initialize the theta parameters for the linear model
theta = np.random.randn(2, 1)
# Define the linear model function
def model(X, theta):
return X.dot(theta)
# Define the cost function
def cost_function(X, y, theta):
m = len(y)
return 1 / (2 * m) * np.sum((model(X, theta) - y)**2)
# Define the gradient calculation function
def grad(X, y, theta):
m = len(y)
return 1 / m * X.T.dot(model(X, theta) - y)
# Define the gradient descent function
def gradient_descent(X, y, theta, learning_rate, n_iterations):
cost_history = np.zeros(n_iterations)
for i in range(n_iterations):
theta = theta - learning_rate * grad(X, y, theta)
cost_history[i] = cost_function(X, y, theta)
return theta, cost_history
# Define the learning rate and number of iterations
learning_rate = 0.2
n_iterations = 20
# Perform gradient descent to optimize the parameters
theta_final, cost_history = gradient_descent(X, y, theta, learning_rate, n_iterations)
# Make predictions with the optimized parameters
predictions = model(X, theta_final)
# Plot the data points and the linear model predictions
plt.scatter(x, y, c='r',label='Data Points')
plt.plot(x, predictions, c='blue',label='Linear Regression Line')
plt.xlabel('Gold Purity')
plt.ylabel('Gold Price')
plt.title('Linear Regression on Gold Price and Gold Purity')
plt.legend()
plt.grid(ls='--')
plt.show()
# Plot the cost history during gradient descent
plt.plot(range(n_iterations), cost_history)
plt.xlabel('Number of Steps')
plt.ylabel('Descent')
plt.title('Descent History during Gradient Descent')
plt.grid(ls='--')
plt.show()
# Calculate the coefficient of determination (R-squared)
def coef_determination(y, pred):
u = ((y - pred)**2).sum()
v = ((y - y.mean())**2).sum()
return 1 - u / v
# Print Final theta
print(theta_final)
# Print the R-squared value
print(coef_determination(y, predictions))
# Display the first 5 samples of the data
print("First 5 samples of the data:")
for i in range(5):
print(f"Sample {i + 1} - Gold Purity: {x[i]:.4f}, Gold Price: {y[i][0]:.4f}")
import numpy as np
import matplotlib.pyplot as plt
# Parameters of the quadratic function
a = 400
b = 200
c = 900
# Generate random data
np.random.seed(42)
x = np.random.uniform(0, 1, 150)
y = a * x**2 + b * x + c + np.random.normal(0, 15, 150)
y = y.reshape(y.shape[0], 1) # Reshaping y to fit the required shape
# Create the feature matrix X
X = np.vstack((x**2,x, np.ones(len(x)))).T
print(X.shape)
# Initialize the theta parameters for the linear model
theta = np.random.randn(3, 1)
# Define the polynomial model function
def model(X, theta):
return X.dot(theta)
# Define the cost function
def cost_function(X, y, theta):
m = len(y)
return 1 / (2 * m) * np.sum((model(X, theta) - y)**2)
# Define the gradient calculation function
def grad(X, y, theta):
m = len(y)
return 1 / m * X.T.dot(model(X, theta) - y)
# Define the gradient descent function
def gradient_descent(X, y, theta, learning_rate, n_iterations):
cost_history = np.zeros(n_iterations)
for i in range(n_iterations):
theta = theta - learning_rate * grad(X, y, theta)
cost_history[i] = cost_function(X, y, theta)
return theta, cost_history
# Define the learning rate and number of iterations
learning_rate = 0.2
n_iterations = 20
# Perform gradient descent to optimize the parameters
theta_final, cost_history = gradient_descent(X, y, theta, learning_rate, n_iterations)
# Make predictions with the optimized parameters
predictions = model(X, theta_final)
# Plot the data points and the polynomial regression predictions
plt.scatter(x, y, c='r', label='Data Points')
plt.plot(x, predictions, c='blue', label='Polynomial Regression Line')
plt.xlabel('Gold Purity')
plt.ylabel('Gold Price')
plt.title('Polynomial Regression on Gold Price and Gold Purity')
plt.legend()
plt.grid(ls='--')
plt.show()
# Plot the cost history during gradient descent
plt.plot(range(n_iterations), cost_history)
plt.xlabel('Number of Steps')
plt.ylabel('Descent')
plt.title('Descent History during Gradient Descent')
plt.grid(ls='--')
plt.show()
# Calculate the coefficient of determination (R-squared)
def coef_determination(y, pred):
u = ((y - pred)**2).sum()
v = ((y - y.mean())**2).sum()
return 1 - u / v
# Print Final theta
print(theta_final)
# Print the R-squared value
print(coef_determination(y, predictions))



