Cómo Construir tu Huésped?
Episodio I
Por Jordan Moles el 2 de enero, 2024

En el centro de este encuentro, una fascinante inmersión en el mundo del Aprendizaje Profundo reserva a los participantes una experiencia sin precedentes, revelando los secretos de la simbiosis entre la tecnología de vanguardia y la imaginación audaz de WestWorld.
En los Confines de la Inteligencia
Bienvenidos, mentes innovadoras, a WestWorld, un parque de atracciones revolucionario donde la innovación tecnológica y la audacia artística se fusionan para crear una experiencia inmersiva sin precedentes. Soy el Dr. Ford, y como Director de este parque de un nuevo tipo, estoy aquí para revelarles los fundamentos computacionales y la visión matemática que sustentan este proyecto extraordinario.


Nuestra ambición va mucho más allá de una simple recreación del Lejano Oeste. WestWorld empuja los límites de la imaginación al presentar huéspedes, androides de una sofisticación sin igual capaces de interactuar de manera indistinguible con nuestros visitantes. No es simplemente entretenimiento; es una exploración de los rincones más profundos de la inteligencia artificial: el Deep Learning.
En el corazón de este paraíso forjado por la tecnología, nuestra búsqueda es empujar constantemente los límites de lo posible. Nuestros huéspedes no simplemente replican acciones preprogramadas; reaccionan, aprenden y evolucionan en tiempo real. Alimentados durante años por una enorme base de datos, los hemos entrenado, validado y sometido a pruebas (aprendizaje supervisado), asegurando que ofrezcan una experiencia única y tengan la capacidad de aprender de manera autónoma después.
Las redes neuronales que los alimentan, inspiradas en la complejidad del cerebro humano, les proporcionan la versatilidad necesaria para realizar una variedad de tareas, desde conducir una carreta hasta montar a caballo, desde leer hasta escribir, desde reconocer a sus semejantes hasta expresar empatía a través del reconocimiento de emociones. Esta sublime unión entre la máquina y el pensamiento humano va más allá de los modelos clásicos de Machine Learning como K-Nearest Neighbors, árboles de decisión o máquinas de vectores de soporte. Cada interacción con un visitante representa una oportunidad para perfeccionar sus habilidades cognitivas (aprendizaje no supervisado), brindando así una experiencia única en cada momento, incluso si este aspecto no se explorará en esta conferencia.
En WestWorld, nuestra vocación no se limita a proporcionar simples entretenimientos; creamos universos virtuales que trascienden la realidad. Para mentes iluminadas como las suyas, destacados participantes en esta empresa, es una expedición a los límites de la tecnología y la humanidad, una fusión entre la creatividad artística y el poder del cálculo avanzado. Nuestro objetivo hoy es iniciarle en los conceptos fundamentales de las redes neuronales presentando el perceptrón multicapa y revelándole el proceso mediante el cual nuestros huéspedes aprenden a reconocer números. En una próxima conferencia, exploraremos en detalle cómo logran identificar a otros individuos. Prepárese para sumergirse en una aventura donde la línea entre el hombre y la máquina se difumina, abriendo horizontes tan vastos como la imaginación misma.

Al Principio: La Neurona Biológica
En un número aproximado de 86 mil millones y conectadas por miles e incluso decenas de miles de sinapsis, estas células altamente especializadas, inscritas en nuestro patrimonio genético desde hace miles de millones de años, se llaman neuronas.
Ensambladas en red, estas neuronas, que calificamos de «biológicas» en contraposición a «artificiales», generan el pensamiento humano y lo que llamamos inteligencia. Sin embargo, no son las únicas células cerebrales en acción. Otros tipos de células desempeñan un papel fundamental y contribuyen al proceso neuronal, siendo su presencia esencial indispensable para la existencia misma de las neuronas.
Su Estructura
La estructura fundamental del sistema nervioso, compuesta por células excitables interconectadas, desempeña un papel crucial en la transmisión de información dentro de nuestra red neuronal. Está compuesta por varios componentes clave que orquestan su función.
Las dendritas actúan como interfaces con el entorno, formando la entrada de la neurona. En gran número, estas extensiones responden a varios estímulos, como la luz en los ojos o la presión sobre la piel, generando descargas eléctricas, también llamadas potenciales de acción, dirigidas hacia el cuerpo celular. La sinapsis, punto de conexión entre las neuronas, desempeña un papel crucial en este lugar, donde la neurona recibe señales de neuronas anteriores o del entorno. Estas señales, ya sean inhibidoras o excitadoras (+1 o -1), convergen hacia la neurona, y cuando su suma supera un umbral crítico, la neurona se activa, produciendo así una señal eléctrica.
El cuerpo celular, central en el proceso, realiza una suma de la intensidad de los impulsos eléctricos provenientes de todas las dendritas. Si esta suma supera un umbral crítico, la neurona se activa y genera una descarga eléctrica transmitida al axón, la única vía de salida de la neurona. Este umbral crítico, que determina la excitación supraumbral, tiene una importancia crucial.
El axón, como la vía final común, se ramifica en múltiples extensiones, conectando la neurona con otras neuronas a través de dendritas y sinapsis. Estos puntos de conexión, representados anatómicamente como hendiduras sinápticas, son esenciales para la transferencia de información entre las neuronas. El extremo del axón, marcado por vesículas de neurotransmisores, libera estos mensajeros químicos en la hendidura sináptica. A su vez, la dendrita de la siguiente neurona, equipada con receptores, captura los neurotransmisores, desencadenando la formación de una corriente eléctrica en la dendrita.
En cuanto a la información transmitida por la neurona, es crucial entender su dualidad electroquímica. Inicialmente creada en forma eléctrica en las dendritas en respuesta a un estímulo, la información se propaga a través del cuerpo celular hacia el axón. En la terminación del axón, el impulso eléctrico desencadena la liberación de neurotransmisores, transformando la información en una forma química en la sinapsis.
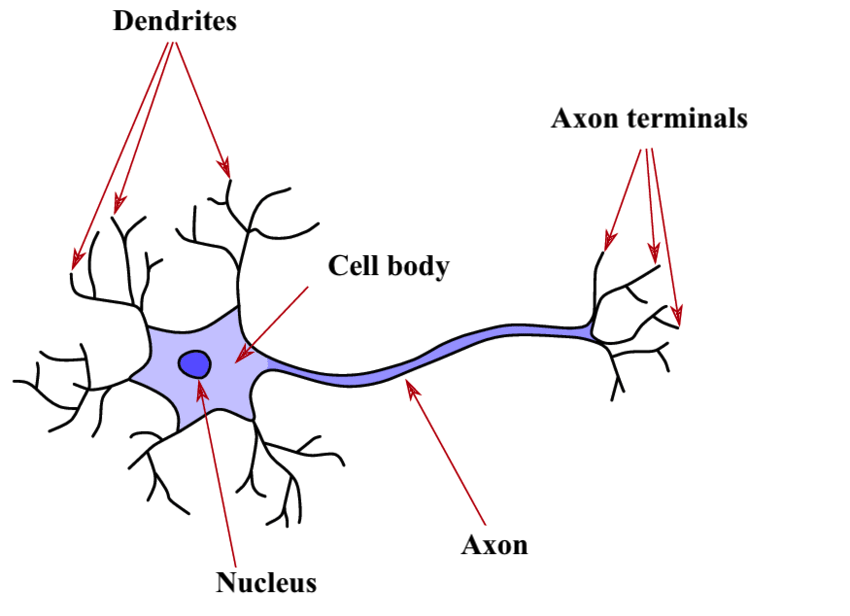

Es importante destacar que esta información circula solo en una dirección específica, desde las dendritas hacia el axón. La dendrita capta la señal, y el axón la difunde, creando así un flujo unidireccional en la información neuronal. Esta sutil danza electroquímica dentro de la neurona forma el fundamento de nuestra comprensión, nuestros pensamientos y nuestra interacción con el mundo que nos rodea.
Su funcionamiento
Pilar del sistema nervioso, se revela como la célula maestra capaz de transmitir señales electroquímicas a lo largo de todo el organismo. Estas señales, resultado de despolarizaciones de la membrana plasmática y la liberación de moléculas químicas en los puntos de conexión con otras células, constituyen el fundamento de la neurotransmisión.
Cada neurona, dedicada a tareas específicas, contribuye a una red compleja que permite realizar funciones tan diversas como la memorización, la motricidad, la facilidad de aprendizaje o incluso el reconocimiento vocal, entre otras.
La variedad de neuronas, reflejando la diversidad de roles que desempeñan, las convierte en actores esenciales en la orquestación compleja de las funciones del sistema nervioso. Estas células, a través de sus extensiones, las dendritas y el axón, establecen conexiones vitales con los órganos inervados y otras neuronas, consolidando así su papel central en las funciones del sistema nervioso.
El Primer Neurona Artificial de la Historia
Estimados oyentes, ahora es el momento oportuno para presentarles la célebre neurona artificial, un concepto importante en informática inaugurado por W. McCulloch y W. Pitt en 1943, una época ya lejana.
Aunque carece de realidad física, este notable elemento ofrece una réplica algorítmica simple de su homólogo biológico, marcando así el comienzo de una fascinante aventura en el mundo de la inteligencia artificial.
Su Estructura y Funcionamiento
La estructura del neurona artificial se caracteriza por varios elementos clave, como la entrada y los pesos sinápticos, el cuerpo celular y la salida. Cada uno de estos aspectos contribuye de manera crucial al procesamiento de la información en las redes de neuronas artificiales. Veámoslo en detalle.
Se Recopila la Información
Comencemos con la entrada. En informática, la entrada representa los datos a procesar, como una cadena de caracteres, una imagen, una densidad de oro o incluso un video.
Cada neurona artificial recibe un número variable de entradas de neuronas aguas arriba, que denominaremos como X. Estas entradas son las señales que activan la neurona y estarán acompañadas de pesos (representados por «w» para «weight») que cuantifican la fuerza de la conexión.
El conjunto de estas entradas forma la primera etapa del procesamiento de la información por la neurona artificial.

El Cuerpo Celular Artificial: una Función Matemática
La fase de agregación. Se asignan pesos sinápticos, inspirados en el funcionamiento de las dendritas, a cada valor de entrada que representa la importancia relativa de las diferentes conexiones para la neurona, luego se suman las entradas ponderadas agregando un sesgo (un valor constante). Por ahora, solo consideramos pesos sinápticos que valen +1 (excitador) o -1 (inhibidor), pero más adelante generalizaremos.
La fase de activación. Luego, una función de activación determina si la neurona debe activarse o no. Primero elegimos una función umbral (llamada Heaviside), es decir, una función que devuelve una salida y=1 si la suma ponderada anterior supera un umbral y 0 en caso contrario (aquí tienes una representación).
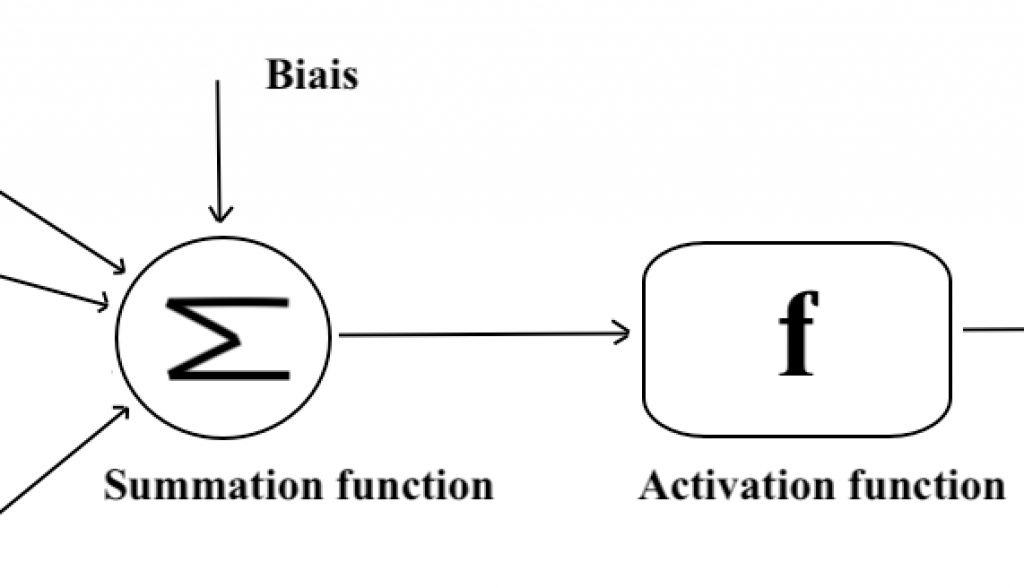
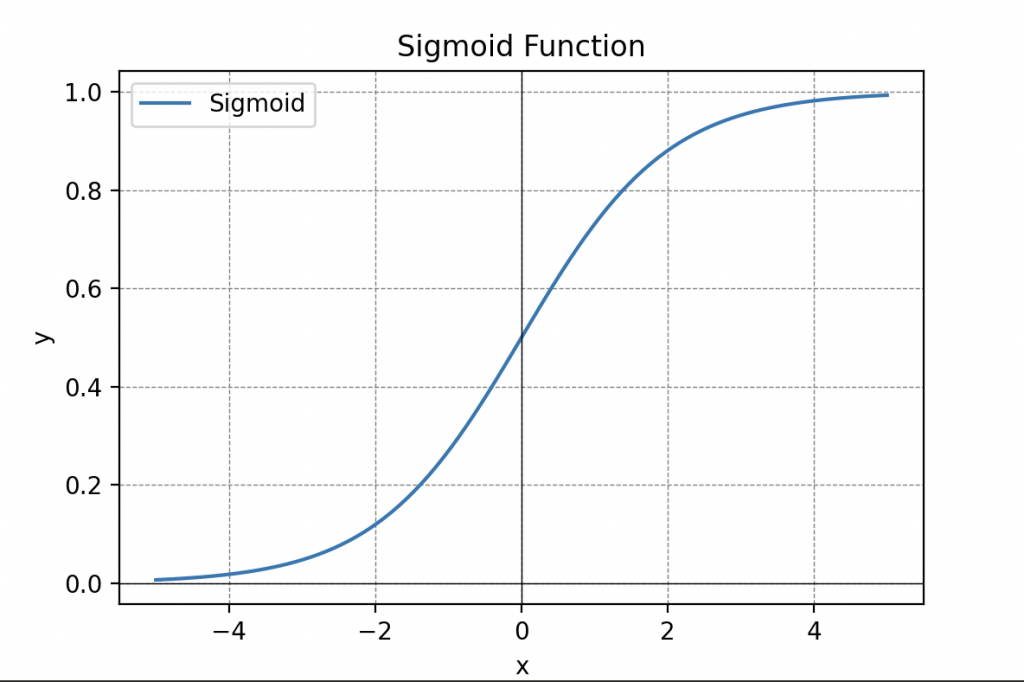
Las funciones de activación son cruciales en el procesamiento de la información y pueden tomar diferentes formas, como la función de umbral, la función sigmoide (recuerdas la sigmoide), la función lineal rectificada (ReLU) o incluso la tangente hiperbólica.



Información Procesada
La salida de la neurona artificial es el resultado final del procesamiento de la información contenida en los datos de entrada X, ya sea y=0 (activado) o y=1 (desactivado). Puede ser transmitida a otras neuronas, formando así una cadena compleja de cálculos que caracteriza el funcionamiento global de la red de neuronas artificiales.



Este primer modelo de neurona artificial fue posteriormente designado como «Unidad de Lógica de Umbral» debido a su capacidad para procesar solo entradas lógicas que valen ya sea 0 o 1. Lograron demostrar que este modelo era capaz de reproducir ciertas funciones lógicas como las compuertas AND y OR (respectivamente Y y O en inglés). Además, al interconectar varias de estas funciones de manera similar a las conexiones entre las neuronas de nuestro cerebro, parecía posible resolver prácticamente cualquier problema de lógica booleana.
A pesar del entusiasmo desmedido generado por este anuncio, quiero asegurarles que, en ese momento, una parte significativa de la comunidad científica pensaba que podríamos desarrollar inteligencias artificiales capaces de reemplazar completamente a los seres humanos.
Científico en la audiencia mirando a los huéspedes junto al Dr. Ford: «¡No estaban completamente equivocados!» Risas en la sala.
El Dr. Ford retoma con una sonrisa: De hecho, no completamente, simplemente que su escala de tiempo no era adecuada para ese anuncio. De todos modos, esa anticipación no se materializó directamente. Aunque este modelo sentó las bases de lo que hoy conocemos como Aprendizaje Profundo, presenta varias deficiencias, como la falta de un algoritmo de aprendizaje. Así, es responsabilidad del usuario determinar manualmente los valores de los parámetros «W» si desea aplicar este modelo a aplicaciones del mundo real.
Un Ejemplo Sencillo
Ahora, comencemos con una breve explicación del álgebra booleana para los dos científicos del fondo.
El álgebra booleana, llamada así por el matemático británico George Boole, es una rama de las matemáticas que se centra en la representación y manipulación de información lógica a través de operaciones en variables llamadas booleanas. Estas variables solo pueden tomar dos valores, generalmente denotados como 0 y 1, simbolizando respectivamente los estados falso (no) y verdadero (sí).
Ampliamente utilizada en informática, electrónica y otros campos relacionados con el procesamiento de información, el álgebra booleana es fundamental para diseñar circuitos lógicos, algoritmos y sirve como base para la lógica proposicional.
En el álgebra booleana, las operaciones fundamentales son el Y lógico, el O lógico y la negación lógica (NO). Estas operaciones se aplican a pares de variables booleanas y producen un resultado booleano.
Un Ejemplo en un Ejemplo
Ahora, para entender mejor estas operaciones, tomemos el ejemplo de una habitación con un interruptor A y un sensor B que detecta la presencia de personas controlando la luz.
Interruptor A Y Sensor B (A Y B):
– Si el interruptor A está activado (A = 1) Y el sensor B detecta personas (B = 1), entonces la condición C «la luz se enciende» es VERDADERA (C = 1).
– Si el interruptor A está desactivado (A = 0), incluso si el sensor B detecta personas (B = 1), la condición C es FALSA (C = 0).
– Si el interruptor A está activado (A = 1) pero el sensor B no detecta personas (B = 0), la condición C también es FALSA (C=0).
– Si ambos, el interruptor A y el sensor B, están desactivados (A=0 y B=0), la condición C es FALSA (C=0).
Interruptor A O Sensor B (A O B):
– Si el interruptor A está activado (A = 1) O el sensor B detecta personas (B = 1), entonces la condición C es VERDADERA (C = 1).
– Si el interruptor A está desactivado (A = 0) O el sensor B detecta personas (B = 1), entonces la condición C es VERDADERA (C = 1).
– Si ambos, si el interruptor A está activado (A = 1) o el sensor B no detecta personas (B = 0), entonces la condición es VERDADERA (C = 1).
– Si el interruptor A está desactivado (A = 0) o el sensor B no detecta personas (B=0), entonces la condición C es FALSA (C = 0).
En estos ejemplos, la operación Y requiere que el interruptor esté activado y que se detecte la presencia de personas para que la condición sea verdadera. Por otro lado, la operación O requiere que el interruptor esté activado o que se detecte la presencia de personas para que la condición sea verdadera.
Todo se puede resumir en estos dos cuadros:
| A | B | A AND B |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
| A | B | A OR B |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
Estas operaciones básicas pueden combinarse para formar expresiones lógicas más complejas, permitiendo representar condiciones (no solo dos como en el ejemplo anterior) y razonamientos lógicos.
El álgebra de Boole encuentra aplicaciones prácticas en el diseño de circuitos lógicos, sistemas de control, informática y otros campos donde la lógica binaria se utiliza para modelar estados y decisiones.
Volvamos al Neurona
El científico del fondo levanta la mano para pedir la palabra: «Pero, ¿qué tiene que ver un neurona con el álgebra de Boole?»
El Dr. Ford entra en detalle en las explicaciones: «Simplifiquemos y consideremos un neurona formal que acepta simplemente dos variables de entrada \(x_1\) y \(x_2\), que colocamos en un vector de entrada (es la información que recibe la neurona):
\begin{equation*} \mathbf{X}=\left[ \begin{array}{c} x_{1} \\ x_{2} \end{array} \right]. \end{equation*}
Dado que las entradas solo pueden tener valores de 0 o 1 en nuestro caso, tenemos solo 4 vectores de entrada posibles:
\begin{equation*} \left[ \begin{array}{c} 0 \\ 0 \end{array} \right]\quad \left[ \begin{array}{c} 0 \\ 1 \end{array} \right]\quad \left[ \begin{array}{c} 1 \\ 0 \end{array} \right]\quad \left[ \begin{array}{c} 1 \\ 1 \end{array} \right] \end{equation*}»
También definimos los dos parámetros sinápticos \(w_1\) y \(w_2\), que también colocamos en un vector que llamamos \(\mathbf{W}\).
\begin{equation*} \mathbf{W}=\left[ \begin{array}{c} w_{1} \\ w_{2} \end{array} \right]. \end{equation*}
Estos pueden tener valores de 1 o -1, por lo que, como anteriormente, tenemos solo 4 vectores de pesos posibles:
\begin{equation*} \left[ \begin{array}{c} -1 \\ -1 \end{array} \right]\quad \left[ \begin{array}{c} -1 \\ 1 \end{array} \right]\quad \left[ \begin{array}{c} 1 \\ -1 \end{array} \right]\quad \left[ \begin{array}{c} 1 \\ 1 \end{array} \right] \end{equation*}

Ahora podemos comenzar la fase de agregación, que toma una entrada, le asocia un peso correspondiente, suma y agrega un sesgo denominado \( b \). Aquí está el resultado:
\[ \Sigma = w_1 x_1 + w_2 x_2 + b \]
Colocamos todo esto en una tabla.
Luego, pasamos a la fase de activación, es decir, introducimos el valor obtenido \( \Sigma \) en nuestra función de umbral que llamaremos \( H \) y que determina la salida de la neurona de la siguiente manera:
\[ y = H(\Sigma + b) \]
Aplicando un razonamiento similar, observamos que una neurona con una sola entrada puede no tener ningún efecto (neurona identidad) o realizar una operación lógica NOT.
Al establecer un vínculo con el álgebra de Boole, hemos demostrado cómo este modelo puede realizar operaciones lógicas fundamentales, como OR y AND.
Sin embargo, a pesar de sus avances, este modelo único presenta dos limitaciones importantes: en primer lugar, está limitado a operaciones simples, y en segundo lugar, no tiene ningún mecanismo de aprendizaje. Como se ilustró anteriormente, las únicas operaciones que podemos realizar son OR y AND, y debemos determinar manualmente los valores de los pesos para realizar estas operaciones lógicas específicas. Estas limitaciones han motivado el desarrollo posterior de modelos más sofisticados en el campo del aprendizaje profundo, especialmente al interconectar estos modelos de neuronas, obtenemos la capacidad de resolver prácticamente cualquier problema de lógica booleana. Además, si permitimos que el modelo aprenda de manera autónoma, se vuelve posible abordar problemas más complejos y ampliar considerablemente sus capacidades.
La Llegada del Perceptrón
El perceptrón, diseñado por el psicólogo estadounidense Frank Rosenblatt unos quince años después de la introducción del concepto de neurona formal por McCulloch y Pitt, representa un avance significativo con la introducción del primer algoritmo de aprendizaje profundo.
El modelo del perceptrón comparte una similitud sorprendente con el que acabamos de estudiar. De hecho, la única diferencia entre el perceptrón y la neurona formal anterior radica en la adición de un algoritmo de aprendizaje que le permite determinar los valores de sus parámetros W para obtener las salidas y deseadas, eliminando así la necesidad de una búsqueda manual por parte de los humanos.
F. Rosenblatt se inspiró en la ley de Hebb en neurociencia, que sugiere que el fortalecimiento de las conexiones sinápticas entre dos neuronas biológicas ocurre cuando se excitan conjuntamente, un fenómeno conocido como el principio «cells that fire together, wire together». Esta plasticidad sináptica es crucial en la construcción de la memoria y el aprendizaje.
La Ley de Hebb
El algoritmo de aprendizaje del perceptrón consiste en entrenar la neurona artificial con datos de referencia (X, y). En cada activación de la entrada X junto con la salida y presente en los datos, los parámetros W se refuerzan. F. Rosenblatt formuló esta idea con la siguiente ecuación:
\[W^* = W + \delta(y_{\text{ref}} – y)X\]
donde los nuevos pesos \(W^*\) se actualizan mediante una tasa de aprendizaje \(\delta\). \(y_{\text{ref}}\) es la salida de referencia, y es la salida producida por la neurona, y X es la entrada de la neurona.
Esta fórmula ajusta los pesos para minimizar la diferencia entre la salida esperada y la salida producida por la neurona. Así, si la neurona produce una salida diferente de la esperada (por ejemplo, y=0 en lugar de y=1), los pesos asociados a las entradas activadas se incrementan. Este proceso continúa hasta que la salida de la neurona converge hacia la salida esperada.
Limites del Modelo
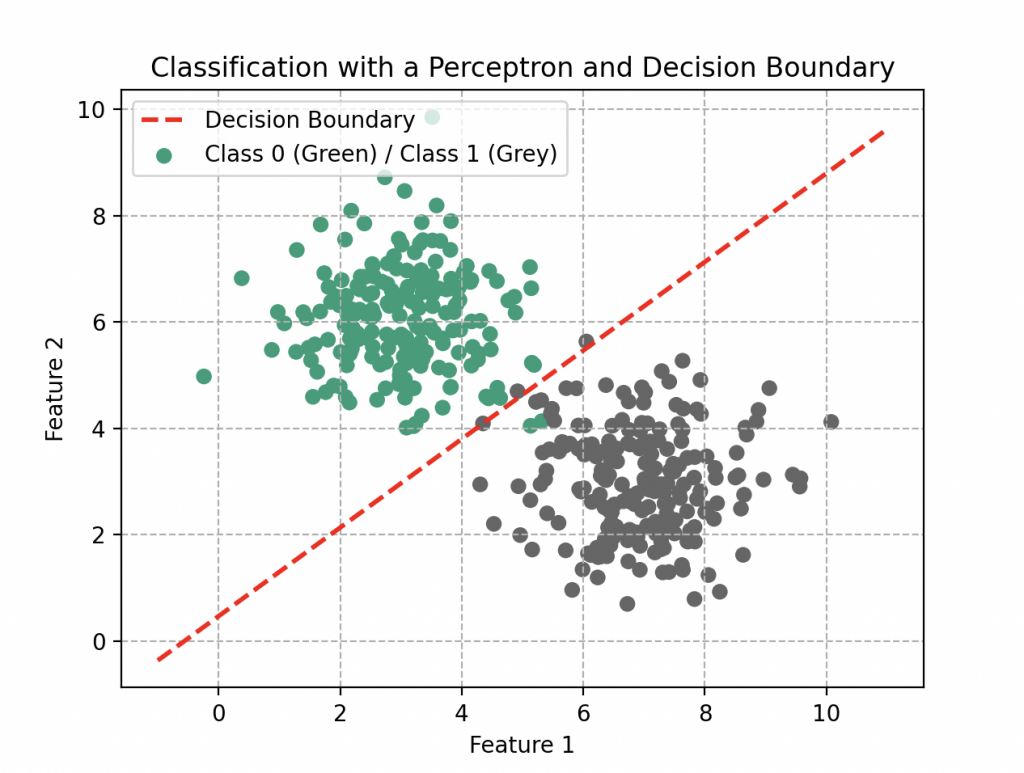
Damas y caballeros de la comunidad científica, consideremos ahora un perceptrón compuesto únicamente por dos entradas \(x_1\) y \(x_2\). Su función de agregación es \(f(x_1, x_2) = w_1x_1 + w_2x_2\) y, por su forma, puede modelar relaciones lineales. Sin embargo, esta simplicidad presenta limitaciones cuando nos enfrentamos a problemas no lineales.
El Dr. Ford destaca con perspicacia: «El perceptrón, en su esencia, es como una herramienta con una perspectiva limitada. Puede tener éxito en realizar predicciones simples, pero lucha por capturar la complejidad de las relaciones no lineales presentes en el mundo real.»
Un científico en la audiencia, mostrando una comprensión profunda: «Es como si estuviéramos tratando de predecir el comportamiento de un círculo trazando solo una línea con la regla.»
Dr. Ford, sonriendo: «¡Exactamente! Es por eso que exploramos enfoques más complejos para modelar la riqueza de las relaciones.»
Algunos Perceptrones Adicionales
Para superar este primer problema, introduzcamos primero tres perceptrones que conectaremos entre sí. Los dos primeros recibirán cada uno las entradas \(x_1\) y \(x_2\), realizarán sus cálculos según sus parámetros y luego enviarán una salida \(y\) al tercer perceptrón. Este último también realizará sus propios cálculos para producir una salida final.

Intente programar tres perceptrones de este huésped y podrá trazar la representación gráfica de la salida final en función de las entradas \(x_1\) y \(x_2\), obteniendo así un modelo no lineal, mucho más interesante.
Este modelo será entonces su primera red de neuronas artificiales, compuesta por 3 perceptrones distribuidos en dos capas: una capa de entrada y una capa de salida. Puede agregar tantas capas y perceptrones como desee, pero cuantos más agregue, más tiempo de cálculo y recursos se requerirán para simular resultados complejos. También puede cambiar la topología, es decir, la naturaleza de las conexiones entre las neuronas. Esto dependerá del problema a resolver. Es lo que vamos a ver ahora.
Las redes neuronales
Las redes neuronales, también conocidas como redes neuronales artificiales, son modelos computacionales inspirados en la estructura y el funcionamiento del cerebro humano. Están compuestas por neuronas artificiales interconectadas y organizadas en capas. Cada neurona recibe entradas, realiza operaciones de procesamiento y luego transmite una salida. Estas salidas se envían luego a las neuronas de la capa siguiente, creando así una arquitectura en capas.
Las redes neuronales comprenden tres tipos principales de capas:
1. Capa de entrada (Input Layer): Recibe los datos de entrada del sistema, donde cada nodo en esta capa representa una característica o variable de entrada.
2. Capas ocultas (Hidden Layers): Estas capas realizan operaciones de transformación de datos. Cada nodo en una capa oculta toma entradas, aplica pesos y sesgos, y luego produce una salida. Son cruciales para que la red aprenda representaciones complejas de los datos.
3. Capa de salida (Output Layer): Produce la predicción o clasificación final, esta capa sintetiza la información aprendida por las capas ocultas para generar la salida final.
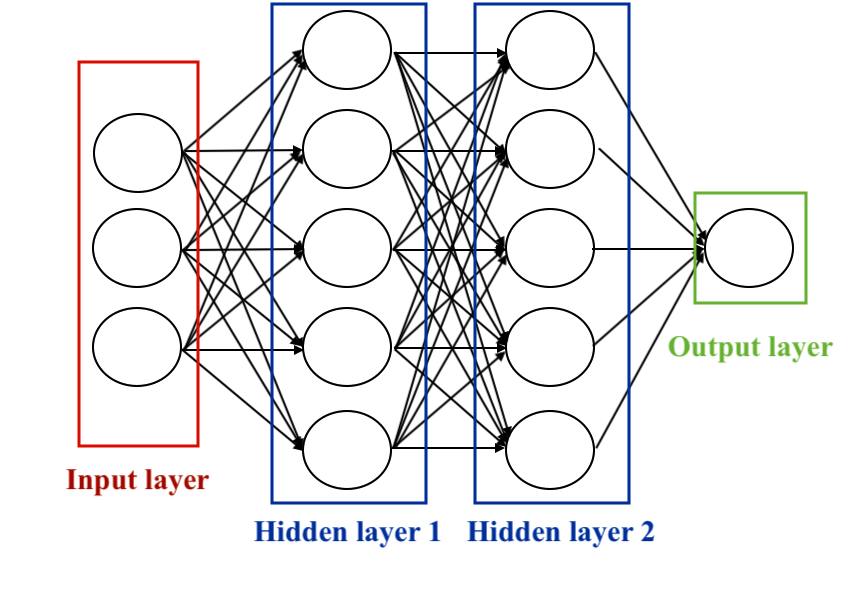
La elección de las unidades ocultas es un área de investigación activa en aprendizaje automático. El número de capas ocultas se llama la profundidad de la red neuronal. La cuestión de cuántas capas hacen que una red sea «profunda» no tiene una respuesta única. En general, las redes más profundas pueden aprender funciones más complejas.
Existen varios tipos de redes neuronales según la topología de las conexiones entre los neuronas. La topología puede variar según la arquitectura específica de la red, pero algunas regularidades son comúnmente observadas. Aquí tienes algunos ejemplos de topologías:
• Perceptrón Multicapa (Multi-layer perceptron): Cada neurona de la capa está conectada a todas las neuronas de la siguiente capa. Es una configuración simple utilizada especialmente para la clasificación de imágenes.
• Red Neuronal Convolucional (Convolutional Neural Network – CNN): Especializada en el procesamiento de imágenes, utiliza filtros para analizar partes locales, reduciendo así el número de parámetros y extrayendo características importantes.
• Red Neuronal Recurrente (Recurrent Neural Network – RNN): Diseñada para procesar datos secuenciales, utiliza conexiones recurrentes para tener en cuenta la secuencia temporal de los datos.
• Memoria a Corto y Largo Plazo (Long Short-Term Memory – LSTM): Una extensión de las RNN, las LSTM procesan secuencias más largas evitando la desaparición del gradiente.
• Autoencoder: Destinada al aprendizaje no supervisado, la red autoencoder consta de una capa de codificación y una capa de decodificación. Su objetivo es reproducir la entrada mientras genera una representación latente. Se centra en la reducción de dimensiones, especialmente útil cuando hay un volumen importante de datos. Al sustituir estos datos por una representación en un espacio de dimensión inferior, se optimiza el procesamiento por los procesadores, mejorando así la eficiencia del modelo (se hablará de esto en otro artículo).
• Red Neuronal Residual (Residual Neural Network – ResNet): Introducidas para resolver el problema de la desaparición del gradiente, las ResNets utilizan conexiones residuales para facilitar el aprendizaje de representaciones más profundas.
En esta exploración, nos centraremos especialmente en las redes neuronales de propagación hacia adelante. Este es el primer tipo de red neuronal artificial, el más simple, donde la información se mueve solo hacia adelante, desde los nodos de entrada hasta los nodos de salida, sin ciclos ni bucles (se dice que es acíclico, distinguiéndose así de las redes recurrentes). El perceptrón solo que ya hemos visto, y luego su extensión más conocida, el perceptrón multicapa que veremos de inmediato.
Pero por cierto, me olvidé, ¿cómo entrenar a una red neuronal para que realice lo que se le pide, es decir, cómo encontrar los parámetros w y b para obtener el modelo correcto?
La audiencia permanece en silencio.
No se preocupen, es ahora cuando veremos eso.
Programación Cognitiva de Huésped de Reconocimiento de Dígitos Manuscritos: el Perceptrón Multicapa
Antes de que nuestros huéspedes puedan sobresalir en tareas más avanzadas, como el reconocimiento de seres humanos o incluso de emociones, es necesario introducirles en las nociones básicas, empezando por el reconocimiento de números escritos a mano, porque como dice el refrán, «antes de aprender a correr, hay que aprender a caminar».
Para guiarles en este aprendizaje (supervisado), utilizamos una serie de imágenes de números, cada una de las cuales representa visualmente la correspondencia entre la forma manuscrita y el número en cuestión.
Nuestros invitados deben reconocer los números que se les presentan.

Este modelo de clasificación constituye la primera red neuronal artificial de nuestros huéspedes, con una capa de entrada, varias capas ocultas por determinar y una capa de salida. Se trata de una red multicapa cuya complejidad puede aumentarse añadiendo más capas y neuronas, pero esto requerirá más tiempo de cálculo.
Ahora vamos a explorar el proceso por el que pasan nuestros huéspedes al programar para dominar esta tarea.
Asimilación de Datos de Entrenamiento (DataSet)
A nuestros huéspedes se les suministran datos de entrenamiento, consistentes en 60.000 ejemplos de imágenes en escala de grises de dígitos manuscritos con una resolución de 28 píxeles por 28 píxeles y sus respectivas correspondencias. Estos datos son cruciales para enseñar a los hosts a generalizar a partir de ejemplos existentes. Y 10.000 imágenes de prueba del mismo formato para examinarlas, es decir, para ver lo bien que han clasificado las imágenes. Aquí están los números del 0 al 9:




Estas imágenes son simplemente matrices de datos que contienen números del 0 al 255. Cada una de las 60.000 matrices se «aplana» para formar 60.000 vectores X con 784 coordenadas correspondientes al número total de píxeles de una imagen con una etiqueta y comprendida entre 0 y 9.
Construcción del Modelo Cognitivo
El modelo cognitivo representa la estructura de la red neuronal en la mente de nuestros huéspedes, abarcando aspectos como el número de capas, el número de neuronas por capa, los parámetros de aprendizaje (W y b) e incluso las funciones de activación. El diseño del modelo depende en gran medida de la naturaleza específica de la tarea.
Los pesos y los sesgos se ajustarán continuamente a lo largo del entrenamiento para minimizar el error entre las predicciones del modelo y los resultados esperados. La inicialización y actualización adecuadas de estos parámetros son cruciales para optimizar el rendimiento de la red. Otros parámetros, como el número de capas y el número de neuronas, se ajustarán manualmente para encontrar el modelo más eficiente en un plazo razonable y sin consumir excesivos recursos, ya que no es deseable que un huéspedes tarde 30 segundos en reconocer un dígito manuscrito o que esté inactivo durante esta tarea.
Propagación hacia delante
La primera etapa de este proceso cognitivo es la propagación hacia delante: el cerebro huéspedes hace circular la información de los píxeles de la primera capa a la última para producir una salida y (la etiqueta manuscrita del dígito).
Analicemos cómo funciona.
• La capa de entrada está formada por 784 neuronas, cada una de las cuales analiza un píxel de la imagen. No tiene parámetros.
• Las capas ocultas (sigmoide): a continuación, dotamos a nuestros huéspedes de dos capas ocultas, cada una de ellas compuesta por 100 neuronas con una función de activación de tipo sigmoide.
La salida de la primera capa es un vector \(A^1\) que contiene 100 coordenadas (una por cada neurona). Los cálculos realizados para cada elemento son sencillos y se basan en el modelo del perceptrón: calculamos la función de agregación y luego le aplicamos la función de activación.

Todo está escrito en forma de matriz compacta.
\begin{align*}
Z^{1} &= W^{1}\cdot X+b^1\\
A^{1} &= \frac{1}{1+\exp{(-Z^{1})}}
\end{align*}
La segunda capa oculta proporciona un vector \(A^2\) que también contiene 100 coordenadas. Hacemos lo mismo para la segunda capa
\begin{align*}
Z^{2} &= W^{2}\cdot A^{1}+b^2\\
A^{2} &= \frac{1}{1+\exp{(-Z^{2})}}
\end{align*}
• La capa de salida: Por último, como el objetivo es clasificar números del 0 al 9, una capa de salida de 10 neuronas, acompañada de una función de activación de tipo softmax, es más que suficiente.
\begin{align*}
Z^{3} &= W^{3}\cdot A^{2}+b^2\\
A^{2} &= \frac{1}{1+\exp{(-Z^{3})}}
\end{align*}
La función softmax asigna probabilidades a cada clase posible. Para cada imagen de entrada, asigna una probabilidad de pertenecer a la clase 0, 1, 2, …, hasta 9. Aquí está un ejemplo

| Números | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|---|---|
| Probabilidades | 0.00000028 | 0.00000000023 | 0.000017 | 0.000070 | 0.00000000019 | 0.00000030 | 0.000000000018 | 0.99 | 0.0000018 | 0.000022 |
Según esta tabla, no hay prácticamente ninguna duda de que este número es el 99% 7, por lo que el host le asignará este número. En general, el huésped asignará a la imagen la etiqueta con mayor probabilidad.
Esta función permite interpretar los resultados como la confianza del modelo en cada clase, y facilita la toma de decisiones en el contexto de una tarea de clasificación multiclase.
Análisis de Errores Cognitivos: la Función de Costes
En la segunda fase, la red neuronal analiza el error entre la salida y del modelo (su predicción) y la salida de referencia esperada (y_{text{ref}}). Esta evaluación se realiza mediante una función de coste frecuentemente utilizada en tareas de clasificación, incluido el reconocimiento de dígitos manuscritos, en este caso la entropía cruzada categórica, que ya hemos encontrado (de otra forma).

Recordemos su expresión:
\begin{align*}L(W,b)=-\frac{1}{n}\sum_{k=1}^n\left[y^{(k)}\log{y_{\text{ref}}}+\left(1-y^{(k)}\right)\log{\left(1-y_{\text{ref}}\right)}\right].\end{align*}
En general, \(y_{ref}\) puede ser la salida final pero también cualquier salida de capa neuronal \(A^{i}\) con i la capa i-ésima que colocamos en una matriz llamada \(\mathbf{A}\). Esto da la siguiente fórmula matricial:
\begin{align*}L(W,b)=-\frac{1}{n}\left[\mathbf{y}\log{\mathbf{A}}+\left(1-\mathbf{y}\right)\log{\left(1-\mathbf{A}\right)}\right].\end{align*}
Es un elemento crucial del análisis cognitivo del modelo y mide la diferencia entre las probabilidades predichas por el modelo y las probabilidades reales de las clases. Su objetivo es cuantificar adecuadamente la discrepancia entre las predicciones de la red neuronal y las verdaderas etiquetas asociadas a las imágenes de los dígitos. La minimización eficiente de esta función de coste durante el entrenamiento ayuda a refinar los parámetros del modelo para obtener un mejor rendimiento.
Comprender los Mecanismos
El tercer paso es la retropropagación. Los huéspedes miden cómo varía esta función de coste en relación con cada capa del modelo, trabajando hacia atrás desde la última a la primera. En otras palabras, analizarán el error en la capa de salida y en la penúltima capa, luego en la penúltima capa y en la penúltima capa, y así sucesivamente, hasta llegar a la capa de entrada.
En resumen, tenemos que calcular cómo se propaga el error de la salida a la entrada para reducirlo. En esta red con dos capas ocultas, esto da 6 expresiones aterradoras (si sólo recuerdas la frase anterior, está bien):
Empezaremos por la última (de la salida a la segunda)
\begin{align*}
\frac{\partial L(\mathbf{W},b)}{\partial \mathbf{W}^3} =\frac{\partial L}{\partial \mathbf{A}^3} \times \frac{\partial \mathbf{A}^3}{\partial \mathbf{Z}^3} \times \frac{\partial \mathbf{Z}^3}{\partial \mathbf{W}^3}
\end{align*}
\begin{align*}
\frac{\partial L(\mathbf{W},b)}{\partial \mathbf{b}^3} =\frac{\partial L}{\partial \mathbf{A}^3} \times \frac{\partial \mathbf{A}^3}{\partial \mathbf{Z}^3} \times \frac{\partial \mathbf{Z}^3}{\partial \mathbf{b}^3}
\end{align*}
penúltimo (penúltimo)
\begin{align*}\frac{\partial L(\mathbf{W},b)}{\partial \mathbf{W}^2} =\frac{\partial L}{\partial \mathbf{A}^3} \times \frac{\partial \mathbf{A}^3}{\partial \mathbf{Z}^3} \times \frac{\partial \mathbf{Z}^3}{\partial \mathbf{A}^2}\times\frac{\partial \mathbf{A}^2}{\partial \mathbf{Z}^2} \times \frac{\partial \mathbf{Z}^2}{\partial \mathbf{W}^2}\end{align*}
\begin{align*}\frac{\partial L(\mathbf{W},b)}{\partial \mathbf{W}^2} =\frac{\partial L}{\partial \mathbf{A}^3} \times \frac{\partial \mathbf{A}^3}{\partial \mathbf{Z}^3} \times \frac{\partial \mathbf{Z}^3}{\partial \mathbf{A}^2}\times\frac{\partial \mathbf{A}^2}{\partial \mathbf{Z}^2} \times \frac{\partial \mathbf{Z}^2}{\partial \mathbf{}^2}\end{align*}
y finalmente la entrada (de la primera a la entrada)
\begin{align*}\frac{\partial L(\mathbf{W},b)}{\partial \mathbf{W}^1} =\frac{\partial L}{\partial \mathbf{A}^3} \times \frac{\partial \mathbf{A}^3}{\partial \mathbf{Z}^3} \times \frac{\partial \mathbf{Z}^3}{\partial \mathbf{A}^2}\times\frac{\partial \mathbf{A}^2}{\partial \mathbf{Z}^2}\times \frac{\partial \mathbf{Z}^2}{\partial \mathbf{A}^1}\times\frac{\partial \mathbf{A}^1}{\partial \mathbf{Z}^1} \times \frac{\partial \mathbf{Z}^1}{\partial \mathbf{W}^1} \end{align*}
\begin{align*}\frac{\partial L(\mathbf{W},b)}{\partial \mathbf{b}^1} =\frac{\partial L}{\partial \mathbf{A}^3} \times \frac{\partial \mathbf{A}^3}{\partial \mathbf{Z}^3} \times \frac{\partial \mathbf{Z}^3}{\partial \mathbf{A}^2}\times\frac{\partial \mathbf{A}^2}{\partial \mathbf{Z}^2}\times \frac{\partial \mathbf{Z}^2}{\partial \mathbf{A}^1}\times\frac{\partial \mathbf{A}^1}{\partial \mathbf{Z}^1} \times \frac{\partial \mathbf{Z}^1}{\partial \mathbf{b}^1} \end{align*}

Optimización Mental
Por último, la cuarta etapa es la optimización mental. Los huéspedes ajustan mentalmente cada parámetro del modelo mediante el descenso de gradiente (¿lo recuerdas? consulta el artículo Wall-E: El Pequeño Minero de Oro), antes de volver a la primera etapa, la propagación hacia delante, para iniciar un nuevo ciclo de entrenamiento.
\begin{align*}\mathbf{W^*}=\mathbf{W}-\delta \frac{\partial }{\partial \mathbf{b}}L(\mathbf{W},\mathbf{b})\\
\mathbf{W^*}=\mathbf{W}-\delta \frac{\partial }{\partial \mathbf{W}}L(\mathbf{W},\mathbf{b})
\end{align*}
con \(\delta\) la tasa de aprendizaje de todas las neuronas.
En resumen, este proceso permite a nuestros huéspedes dominar hasta cierto punto el reconocimiento de dígitos manuscritos, con una tasa de éxito de alrededor del 83%, aunque este rendimiento no es excepcional. He aquí algunos de los errores que cometen nuestros huéspedes:


Es evidente que algunos números manuscritos pueden resultar confusos, incluso para el ojo humano, mientras que otros parecen inequívocamente identificables, como el 3 anterior.

Así, ajustando unos pocos parámetros, resulta relativamente fácil mejorar significativamente el rendimiento del modelo y alcanzar una precisión del 94%, una habilidad crucial en su camino hacia la adquisición de tareas cognitivas más avanzadas.
A medida que nuestros invitados progresen, ampliarán sus áreas de especialización, abriendo nuevas posibilidades para experiencias más inmersivas en Westworld.
Los Huéspedes de Westworld: de los Números a las Caras
En conclusión, mis queridos invitados, nuestra primera exploración de los misterios del Aprendizaje Profundo termina aquí. Estoy encantado de haberles desvelado una serie de conceptos, como las neuronas formales, los perceptrones y los perceptrones multicapa. Hemos analizado un ejemplo concreto en el que los huéspedes de Westworld, utilizando sus procesadores, han adquirido la capacidad de reconocer e interpretar números escritos a mano con una precisión desconcertante.
Pero no nos equivoquemos, esta red neuronal por sí sola dista mucho de ser suficiente cuando el mundo que hay que analizar tiene una resolución mayor. El número de parámetros de entrenamiento que había que ajustar para nuestro perceptrón multicapa (¡eran muchos! 89.610 parámetros) de sólo dos capas ocultas de 100 neuronas era relativamente pequeño para funcionar en máquinas de bajo consumo. Ahora imagine simular un modelo así con cientos de capas y miles de neuronas por capa. Sería imposible. Por eso se han desarrollado otras técnicas, como las redes neuronales convolucionales, que utilizan filtros para analizar elementos característicos de la imagen.
Por último, y lo dejo aquí, no visualicemos como «inteligente» una inteligencia artificial que discierne rostros, objetos complejos o emociones. Porque aunque los huéspedes parezcan acercarse asombrosamente a la humanidad en sus interacciones, recordemos siempre que no son más que máquinas.
Dr. Ford - "Recuerda, los huéspedes no son reales. No son conscientes."

Bibliografía
F. Rosenblatt, The Perceptron, A perceiving and recognizing automaton, Cornell Aeronautical Laboratory, 1957
F. Rosenblatt, The Perceptron: A Probabilistic Model For Information Storage And Organization in the Brain, Psychological Review, vol. 65, no 6, 1958
M. Tommasi, Le Perceptron, Apprentissage automatique : les réseaux de neurones, cours à l’université de Lille 3.
D.B. Parker, Learning Logic , Massachusetts Institute of Technology, Cambridge MA, 1985.
G. Saint-Cirgue, Machine Learnia, Youtube Channel.
USI Events, Deep learning, Yann LeCun on Youtube.
Nota: para más información sobre el código proporcionado, visite GitHub. Enlace en el pie de página.
import numpy as np
import matplotlib.pyplot as plt
# Set the random seed for reproducibility
np.random.seed(42)
# Generate points for class 0
class0_points = np.random.normal(loc=[3, 6], scale=[1, 1], size=(200, 2))
# Generate points for class 1
class1_points = np.random.normal(loc=[7, 3], scale=[1, 1], size=(200, 2))
M0 = np.zeros((class0_points.shape[0], 1))
M1 = np.ones((class1_points.shape[0], 1))
X = np.concatenate([class0_points, class1_points], axis=0)
y = np.concatenate([M0, M1], axis=0)
# Create an initialization function to initialize parameters W and b of our model
def initialization(X):
np.random.seed(seed=0)
W = np.random.randn(X.shape[1], 1)
b = np.random.randn(1)
return W, b
W, b = initialization(X)
print(W.shape)
# Next, create an iterative algorithm where we repeat the following functions in a loop:
# Start with the function that represents our artificial neuron model, where we find the function Z = X.W + b and the activation function A
def model(X, W, b):
Z = X.dot(W) + b
A = 1 / (1 + np.exp(-Z))
return A
A = model(X, W, b)
# Next, create an evaluation function, i.e., the cost function that evaluates the model's performance by comparing the output A to the reference data y
def log_loss(A, y):
return (1 / len(y)) * np.sum(-y * np.log(A) - (1 - y) * np.log(1 - A))
# In parallel, calculate the gradients of this cost function
def gradients(A, X, y):
dW = (1 / len(y)) * np.dot(X.T, A - y)
db = (1 / len(y)) * np.sum(A - y)
return dW, db
dW, db = gradients(A, X, y)
print(dW.shape)
print(db.shape)
# Finally, use these gradients in an update function that updates the parameters W and b to reduce the model's errors
def update(dW, db, W, b, learning_rate):
W = W - learning_rate * dW
b = b - learning_rate * db
return W, b
# Create a prediction function
def predict(X, W, b):
A = model(X, W, b)
return A >= 0.5
# Create an artificial neuron
def artificial_neuron(X, y, learning_rate=0.1, n_iter=100):
# Initialize W, b
W, b = initialization(X)
# Visualize the loss
Loss = []
# Create a training loop
for i in range(n_iter):
A = model(X, W, b)
Loss.append(log_loss(A, y))
dW, db = gradients(A, X, y)
W, b = update(dW, db, W, b, learning_rate)
# Calculate predictions for all data
y_pred = predict(X, W, b)
# Display the performance of our model (e.g., accuracy), comparing the reference data y with our predictions
# print(accuracy_score(y, y_pred))
# Visualize the loss to see if our model has learned well
plt.plot(Loss)
plt.grid(ls='--')
plt.show()
return W, b
# Train the artificial neuron
W, b = artificial_neuron(X, y)
# Test on new data
new_data = np.array([6, 4])
plt.scatter(X[:, 0], X[:, 1], c=y, cmap='Dark2', label='Class 0 (Blue) / Class 1 (Orange)')
plt.scatter(new_data[0], new_data[1], c='red', label='New Data (Red)')
plt.title('Classification with an Artificial Neuron')
plt.xlabel('Feature 1')
plt.ylabel('Feature 2')
plt.grid(ls='--')
plt.legend()
plt.show()
prediction = predict(new_data, W, b)
print(f"Prediction for new data: {prediction}")
# Create the decision boundary
x0 = np.linspace(-1, 11, 100)
x1 = (-W[0] * x0 - b) / W[1]
plt.plot(x0, x1, c='red', lw=2, ls='--', label='Decision Boundary')
plt.scatter(X[:, 0], X[:, 1], c=y, cmap='Dark2', label='Class 0 (Green) / Class 1 (Grey)')
plt.title('Classification with a Perceptron and Decision Boundary')
plt.xlabel('Feature 1')
plt.ylabel('Feature 2')
plt.grid(ls='--')
plt.legend()
plt.show()
import numpy as np
import matplotlib.pyplot as plt
from tqdm import tqdm
from sklearn.metrics import log_loss, accuracy_score
from keras.datasets import mnist
from sklearn.preprocessing import OneHotEncoder
# Load MNIST data
(X_train, y_train), (X_test, y_test) = mnist.load_data()
# Display one image for each digit
fig, ax = plt.subplots(nrows=1, ncols=10, figsize=(20, 4))
for digit in range(10):
digit_indices = np.where(y_train == digit)[0]
ax[digit].imshow(255 - X_train[digit_indices[0]], cmap='gray')
ax[digit].set_title(f'Digit {digit}')
ax[digit].axis('off')
plt.tight_layout()
plt.show()
# Reshape and normalize input data
X_train_reshape = X_train.reshape(X_train.shape[0], -1) / 255.0
X_test_reshape = X_test.reshape(X_test.shape[0], -1) / 255.0
# Transpose labels if needed
y_train = y_train.reshape(-1, 1)
y_test = y_test.reshape(-1, 1)
# One-hot encode labels
encoder = OneHotEncoder(sparse=False, categories='auto')
y_train_onehot = encoder.fit_transform(y_train)
y_test_onehot = encoder.transform(y_test)
# Select a subset of data
m_train = 5000
m_test = 1000
X_train_reshape = X_train_reshape[:m_train, :]
X_test_reshape = X_test_reshape[:m_test, :]
y_train_onehot = y_train_onehot[:m_train, :]
y_test_onehot = y_test_onehot[:m_test, :]
print(X_train_reshape.shape)
print(X_test_reshape.shape)
print(y_train_onehot.shape)
print(y_test_onehot.shape)
# Neural network initialization function
def initialization(dimensions):
np.random.seed(seed=0)
parameters = {}
C = len(dimensions)
for c in range(1, C):
parameters['W' + str(c)] = np.random.randn(dimensions[c], dimensions[c-1])
parameters['b' + str(c)] = np.random.randn(dimensions[c], 1)
return parameters
# Neural network forward propagation function
def forward_propagation(X, parameters):
activations = {'A0': X}
C = len(parameters) // 2
for c in range(1, C + 1):
Z = parameters['W' + str(c)].dot(activations['A' + str(c-1)]) + parameters['b' + str(c)]
activations['A' + str(c)] = 1 / (1 + np.exp(-Z))
return activations
# Neural network backpropagation function
def back_propagation(X, y, activations, parameters):
m = y.shape[1]
C = len(parameters) // 2
dZ = activations['A' + str(C)] - y
gradients = {}
for c in reversed(range(1, C + 1)):
gradients['dW' + str(c)] = (1/m) * np.dot(dZ, activations['A' + str(c-1)].T)
gradients['db' + str(c)] = (1/m) * np.sum(dZ, axis=1, keepdims=True)
if c > 1:
dZ = np.dot(parameters['W' + str(c)].T, dZ) * activations['A' + str(c-1)] * (1 - activations['A' + str(c-1)])
return gradients
# Neural network update function
def update(gradients, parameters, learning_rate):
C = len(parameters) // 2
for c in range(1, C + 1):
parameters['W' + str(c)] = parameters['W' + str(c)] - learning_rate * gradients['dW' + str(c)]
parameters['b' + str(c)] = parameters['b' + str(c)] - learning_rate * gradients['db' + str(c)]
return parameters
# Neural network prediction function
def predict(X, parameters):
activations = forward_propagation(X, parameters)
C = len(parameters) // 2
Af = activations['A' + str(C)]
return (Af >= 0.5).astype(int)
# Neural network training function
def neural_network(X, y, hidden_layers=(100, 100), learning_rate=0.1, n_iter=1000):
np.random.seed(0)
dimensions = [X.shape[0]] + list(hidden_layers) + [y.shape[0]]
parameters = initialization(dimensions)
train_loss = []
train_acc = []
for i in tqdm(range(n_iter)):
activations = forward_propagation(X, parameters)
gradients = back_propagation(X, y, activations, parameters)
parameters = update(gradients, parameters, learning_rate)
if i % 10 == 0:
C = len(parameters) // 2
train_loss.append(log_loss(y, activations['A' + str(C)]))
y_pred = predict(X, parameters)
current_accuracy = accuracy_score(y.flatten(), y_pred.flatten())
train_acc.append(current_accuracy)
plt.figure(figsize=(12, 4))
plt.subplot(1, 2, 1)
plt.plot(train_loss, label='train loss')
plt.legend()
plt.subplot(1, 2, 2)
plt.plot(train_acc, label='train acc')
plt.legend()
plt.show()
return parameters
# Train the neural network
parameters = neural_network(X_train_reshape.T, y_train_onehot.T, hidden_layers=(100, 100), learning_rate=0.1, n_iter=5000)
# Predict on test data
y_pred = predict(X_test_reshape.T, parameters)
# Print accuracy on test data
test_accuracy = accuracy_score(y_test_onehot.flatten(), y_pred.flatten())
print(f"Test Accuracy: {test_accuracy}")
import numpy as np
import tensorflow as tf
import keras
import matplotlib.pyplot as plt
from keras.datasets import mnist
# Load MNIST data
(X_train, y_train), (X_test, y_test) = mnist.load_data()
# Display one image for each digit
fig, ax = plt.subplots(nrows=1, ncols=10, figsize=(20, 4))
for digit in range(10):
digit_indices = np.where(y_train == digit)[0]
ax[digit].imshow(255 - X_train[digit_indices[0]], cmap='gray')
ax[digit].set_title(f'Digit {digit}')
ax[digit].axis('off')
plt.tight_layout()
#plt.show()
# Reshape and normalize input data
X_train = X_train/ 255.0
X_test = X_test / 255.0
hidden1 = 100
hidden2 = 100
model = keras.Sequential([
keras.layers.Input((28, 28)),
keras.layers.Flatten(),
keras.layers.Dense(hidden1, activation='relu'),
keras.layers.Dense(hidden2, activation='relu'),
keras.layers.Dense(10, activation='softmax')
])
model.compile(optimizer='adam',
loss='sparse_categorical_crossentropy',
metrics=['accuracy'])
batch_size = 512
epochs = 16
history = model.fit(X_train, y_train,
batch_size=batch_size,
epochs=epochs,
verbose=1,
validation_data=(X_test, y_test))
# Plot the training history
plt.plot(history.history['accuracy'], label='train accuracy')
plt.plot(history.history['val_accuracy'], label='validation accuracy')
plt.xlabel('Epochs')
plt.ylabel('Accuracy')
plt.legend()
#plt.show()
plt.plot(history.history['loss'], label='train loss')
plt.plot(history.history['val_loss'], label='validation loss')
plt.xlabel('Epochs')
plt.ylabel('Loss')
plt.legend()
#plt.show()
# Evaluate the model on the test set
score = model.evaluate(X_test, y_test, verbose=0)
print('Test Loss:', score[0])
print('Test Accuracy:', score[1])
# Predictions on the test set
y_pred = model.predict(X_test)
y_pred_classes = np.argmax(y_pred, axis=-1)
print(y_pred[0])
plt.figure(figsize=(20, 4))
plt.imshow(255 - X_test[0], cmap='gray')
plt.title(f'Digit: {y_test[0]}')
plt.axis('off')
plt.show()
print(model.summary())



