Derrota al maestro del juego
Por Jordan Moles el 2 de octubre de 2023

En el corazón de una taberna sombría, perdida en algún lugar de un extraño multiverso de Dungeons and Dragons, se reunió un grupo de individuos tan diversos como ruidosos. Las risas atronadoras resonaban en el ahumado local, mientras dados de todas las formas giraban por el aire, deteniéndose con un satisfactorio golpe para determinar el destino de sus dueños. Sentados en taburetes tambaleantes alrededor de una antigua mesa de madera desgastada por el tiempo, nuestros héroes, o al menos lo que se podría llamar así, se preparaban para una merecida noche de cerveza, dados y camaradería.
¡Hagamos las presentaciones!
En el centro de esta reunión ecléctica se encontraba el Ranger, autoproclamado líder del equipo.
Su principal misión era mantener la paz dentro del grupo, especialmente entre el Elfo y el Enano, dos individuos conocidos por sus desacuerdos.
Sin embargo, a pesar de sus esfuerzos, a menudo se sentía abrumado por la desesperación, especialmente cuando las cosas salían mal. El Guardabosques no estaba especializado en ninguna habilidad en particular, sino que era versátil.
Tenía la desafortunada costumbre de sobreestimar sus habilidades y de intentar usar talentos que no dominaba por completo.


A su izquierda, se encontraba el Bárbaro.
Era una figura colosal con músculos prominentes, empuñando una espada como una extensión de su poderoso brazo. La vida del Bárbaro se reducía a dos pasiones: el combate y la juerga con el Enano.
No sentía ningún afecto por la magia, que consideraba una debilidad. A menudo, estaba dispuesto a juzgar a los demás miembros del grupo como cobardes si no compartían su pasión por el combate cuerpo a cuerpo.
Del otro lado de la mesa, la Elfa descansaba con gracia natural. Con su belleza encantadora, parecía estar libre de preocupaciones. Su comportamiento despreocupado y alegre contrastaba fuertemente con el de sus compañeros.
A menudo, su comportamiento era considerado excéntrico, aunque parecía no darse cuenta de ello.
Mantenía una relación tumultuosa con el Enano, y su mutua antipatía se había vuelto legendaria entre los habituales de la taberna.


Junto al Bárbaro, el Enano, un guerrero robusto y colérico, se preparaba para entrar en la arena del inminente juego. Su obsesión principal era el dinero, y estaba dispuesto a hacer cualquier cosa para llenar su bolsa, incluso embarcarse en aventuras peligrosas con compañeros que no soportaba, especialmente la Elfa, con quien tenía una relación abominable.
El Enano también era un experto en cálculos complejos, especialmente cuando se trataba de distribuir el botín entre los miembros del grupo, teniendo en cuenta diversos criterios como el tiempo pasado juntos, el peligro de las situaciones y la experiencia adquirida en las batallas.
Nunca desaprovechaba la oportunidad de saborear buenos jamones y blandir su pequeña hacha, que manejaba con gran destreza.
En las sombras, el Ladrón, vestido discretamente, observaba la escena. Sus agudos ojos escudriñaban en busca de la próxima bolsa para robar.
Su legendaria agilidad y destreza lo convertían en un maestro en el arte del robo, pero también significaba que no podía resistirse a hurtar pequeñas cosas, incluso entre sus compañeros.
Su actitud sombría y túnica de cuero negro apenas dejaban rastro mientras se deslizaba en las sombras. Sus herramientas de ganzúas, robo y espionaje estaban cuidadosamente ocultas bajo un discreto cinturón.


Junto a la Elfa, se encontraba la Maga. Era una mujer de cabello rojo profundo, apasionada por todo tipo de literatura, con una fascinación particular por los libros de hechizos.
Desafortunadamente, sus talentos mágicos eran limitados, y no destacaba particularmente en ese ámbito. A pesar de su falta de aptitud mágica, lo compensaba con su profundo conocimiento de los libros.
En cuanto a su vestimenta, solía llevar una larga túnica de color azul oscuro adornada con motivos plateados que se asemejaban a estrellas centelleantes. Su atuendo se complementaba con un sombrero puntiagudo a juego, que añadía un toque de misterio a su apariencia. También llevaba un cinturón de cuero con bolsillos para guardar pequeños objetos mágicos y componentes para sus hechizos.
La Maga seguía siendo una fuente inestimable de conocimiento para el grupo y desempeñaba un papel central en la compañía, compartiendo eficazmente el liderazgo con el Guardabosques.
Finalmente, a su lado se encontraba el Ogro, una criatura imponente. Su apetito insaciable se manifestaba en gruñidos primitivos. Aunque tenía una naturaleza amable, seguía siendo una fuente constante de problemas, volcando sillas y rompiendo vasos a intervalos regulares.
Sus acciones estaban principalmente dictadas por instintos, lo que lo acercaba al Bárbaro, con quien compartía una pasión por la buena comida. Sin embargo, tenía una conexión especial con la Maga, la única capaz de entender su lenguaje.

Las Reglas del Juego
Después de varias jarras de cerveza, acaloradas discusiones, chistes cuestionables y anécdotas épicas, el ambiente en la taberna estaba en su punto máximo. Las risas estruendosas y el canto desafinado de los aventureros llenaban la habitación, mientras las camareras abrumadas intentaban atender los pedidos que no dejaban de aumentar.
La Maga, impulsada por el ambiente festivo, decidió que era el momento de añadir un toque extra de emoción a la noche. De repente, sacó un conjunto de 14 dados misteriosos de su bolso, 2 de cada tipo, captando de inmediato la atención de sus compañeros. Miradas curiosas se posaron en los dados mientras las conversaciones se apaciguaban gradualmente.
Con una sonrisa traviesa iluminando su rostro, anunció en voz alta: «Amigos míos, vamos a darle sabor a esta noche con un juego de dados. ¿Quién está listo para probar su suerte?»
El anuncio de la Maga generó una ola de entusiasmo entre los aventureros ya un poco ebrios.
El Enano, siempre ansioso por oportunidades para ganar oro pero renuente a apostar el suyo propio, golpeó la mesa con sus manos curtidas y exclamó: «¡Por las barbas de nuestros antepasados, yo participo!»
La Elfa, a pesar de sus frecuentes desacuerdos con el Enano, sonrió y dijo: «¿Por qué no? Podría ser divertido.»
Incluso el Ogro, cuya expresión facial limitada no revelaba mucho, emitió un gruñido de consentimiento.
El Ranger, seguido por el Bárbaro y el Ladrón, fue rápidamente a buscar suministros, una tabla de quesos y un poco de jamón del país antes de escuchar atentamente las reglas del juego.
La Maga, encantada de ver que su idea había sido tan bien recibida, rebuscó en su bolso y sacó un pergamino grande. Contenía las leyes fundamentales que debían leerse antes de jugar. Estaban escritas de una manera peculiar, pareciendo runas que solo la Maga podía descifrar, pero aquí está la nota transcrita mágicamente a nuestro idioma:
Querido mortal, ten cuidado, pues te iniciaré en los profundos misterios que gobiernan estos dados sagrados. Están sujetos a leyes enigmáticas que debes comprender antes de desatarlos sobre la mesa. Sigue mis palabras con cuidado y descubrirás el poder oculto detrás de cada lanzamiento. Aquí tienes la más importante, aquella que los define a todos.
Sea (\(\Omega\), A) un espacio medible, donde \(\Omega\) es el universo y A es una sigma-álgebra. Una medida de probabilidad es una medida con una masa total de 1 y cumple con los siguientes tres axiomas:
• Para cualquier conjunto E en A, la probabilidad \(\mathbb{P}\)(E) es un número real entre 0 y 1.
• La probabilidad del universo \(\Omega\) es igual a 1, es decir, \(\mathbb{P}(\Omega) = 1\).
• La probabilidad es \(\sigma\)-aditiva, lo que significa que para cualquier familia finita o numerable de conjuntos mutuamente disjuntos \((E_i, i \in I)\) en A, la probabilidad de su unión es igual a la suma de las probabilidades individuales:
\begin{equation*}\mathbb{P}\left(\bigcup_{i\in I} E_i\right) = \sum_{i\in I} \mathbb{P}(E_i)\end{equation*}
En particular, la probabilidad del conjunto vacío (\(\emptyset\)) es igual a 0, es decir, \(\mathbb{P}(\emptyset) = 0\).
El Elfo, el Bárbaro y el Guardabosques se rascan la cabeza confundidos, mientras que el Enano, siempre atento a la perspectiva de ganar oro, asiente en silencio. La Maga, al ver que sus explicaciones no han sido comprendidas por todos, decide simplificar aún más.
Saca un pequeño trozo de papel de su bolsillo y comienza a explicar de manera más concisa: «De acuerdo, olvidemos los términos complicados. El universo es simplemente todos los resultados posibles. Por ejemplo, cuando lanzamos un dado, los resultados posibles son 1, 2, 3, 4, 5 y 6. Eso es el universo, que representamos como \(\Omega=\{1, 2, 3, 4, 5, 6\}\).
Luego, un sigma-álgebra es el conjunto de todos los subconjuntos del universo, es decir, todos los posibles grupos de resultados que podemos obtener. Por ejemplo, un subconjunto podría ser el conjunto de números pares, que es \(\{2, 4, 6\}\).
¿Me siguen hasta ahora?
Pasemos a los axiomas. El primero es simple: simplemente dice que la probabilidad de un evento siempre está entre 0 y 1. En otras palabras, esto significa que la probabilidad de obtener un resultado siempre es o cero (imposible) o uno (cierto).
El segundo axioma es aún más simple. Dice que la probabilidad total de todos los resultados posibles siempre es 1. Entonces, si sumamos la probabilidad de obtener cada número en nuestro dado, siempre debe ser igual a 1.
El tercer axioma, un poco más complejo, significa que si tenemos dos eventos que no pueden ocurrir al mismo tiempo (disjuntos), entonces la probabilidad de que ocurra cualquiera de ellos es simplemente la suma de las probabilidades de cada uno. Por ejemplo, la probabilidad de obtener un 1 o un 6 al lanzar un dado justo es la suma de la probabilidad de obtener un 1 y la probabilidad de obtener un 6.
Espero que esto aclare un poco las cosas.»
La Maga, consciente de que sus compañeros están empezando a impacientarse con los términos técnicos, decide simplificar aún más las explicaciones para hacer que los conceptos sean más accesibles.
Continúa su narración: «Ahora, olvidemos los términos complejos por un momento. Las leyes de la probabilidad se pueden describir en tres categorías principales de características, como se indica en este pergamino:»
•«Hay parámetros de posición que influyen en la tendencia central de la distribución de probabilidad. Estos determinan los valores alrededor de los cuales la probabilidad está más concentrada, es decir, donde la mayoría de los resultados se agrupan. Entre estos parámetros, tenemos la esperanza, que es una medida del promedio, la mediana, que es el valor central, y la moda, que es el valor más frecuente.»
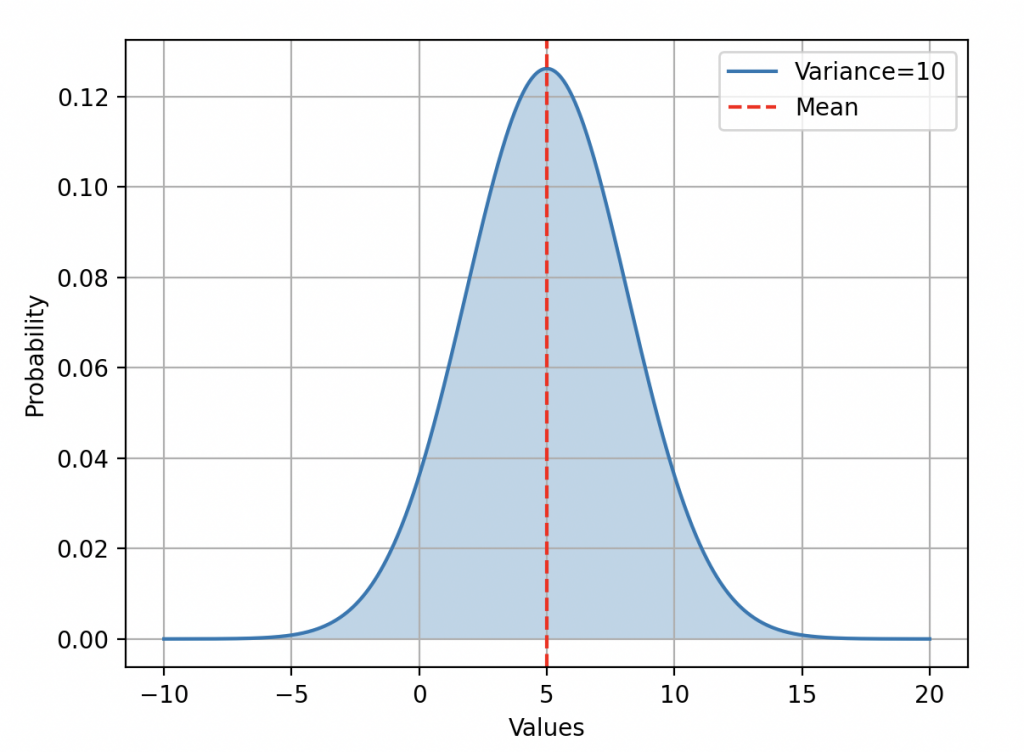
Distribución normal con una media de 5 y una varianza de 10.

• «Luego, existen parámetros de escala que miden qué tan dispersos o agrupados están los valores alrededor de esos valores centrales. La varianza, la desviación estándar y el rango intercuartil son ejemplos de estos parámetros. A menudo nos enfocamos en la varianza, que funciona de la siguiente manera:
Si está cerca de cero, sugiere que los valores individuales son similares y se agrupan estrechamente alrededor de la media.
Por otro lado, una varianza alta indica que los valores individuales están más alejados de la media, con una mayor dispersión en general.»


Dos leyes de distribución normal con una media igual a 5 y una varianza igual a 2, y la otra con una media igual a 20.
• «Finalmente, tenemos los parámetros de forma. Describen cómo cambian las probabilidades a medida que nos alejamos de los valores centrales.
Por ejemplo, la asimetría mide si la distribución está inclinada hacia un lado u otro, y el curtosis, o el coeficiente de curtosis, examina cuán cerca están concentrados los valores cerca de la media.«

Distribución normal con asimetría cero y distribución normal con asimetría igual a 10.

La Ley del Dado
La Maga hizo una pausa antes de concluir: «Ahora que hemos repasado estos conceptos, adentrémonos en el meollo de lo que parece interesarles: la distribución de probabilidad discreta uniforme.»
Elfo: (susurrándole al Bárbaro) Ya era hora; casi es hora de dormir.
Bárbaro: (riendo) Sí, espero que esta lección magistral termine antes de medianoche.
Ranger: (sonriendo) Tal vez deberíamos preparar algunas mantas para nuestros compañeros cansados.
La Maga, mirándolos con una expresión divertida, decide continuar a pesar de las bromas de sus compañeros.
La Maga: La distribución discreta uniforme es quizás la distribución de probabilidad más importante que necesitan entender aquí. Asegura la equiprobabilidad, lo que significa que cada resultado tiene una probabilidad igual para cada modo en un conjunto finito de modos posibles.
El Enano pierde la paciencia con toda la jerga y arrebata el pergamino de las manos de la Maga.
El Enano: (frunciendo el ceño) Espera… ¿dice este viejo pergamino que debería darte una moneda de oro? No estoy seguro de por qué debería hacerlo.
El Bárbaro: (riendo) ¡Jaja! ¡El pergamino predice el futuro! Vamos, Enano, dale la moneda.
El Enano se niega a entregar su moneda, pero el impaciente Bárbaro le da un puñetazo en la cabeza.
El Bárbaro: (riendo) ¡Vamos, Enano, hazlo por la educación! Solo cuesta una moneda.
El Ogro: (golpeando la mesa y riendo a carcajadas), Zog zog.
La Elfa: Bien hecho.
El Enano, ligeramente aturdido por el golpe, a regañadientes entrega una moneda de oro a la Maga junto con el pergamino.
Maga: Perfecto, gracias por tu contribución. Entonces, para entender mejor, imaginen una moneda justa. Cuando la lanzas, cada lado tiene una probabilidad igual de aparecer, que es 1/2.
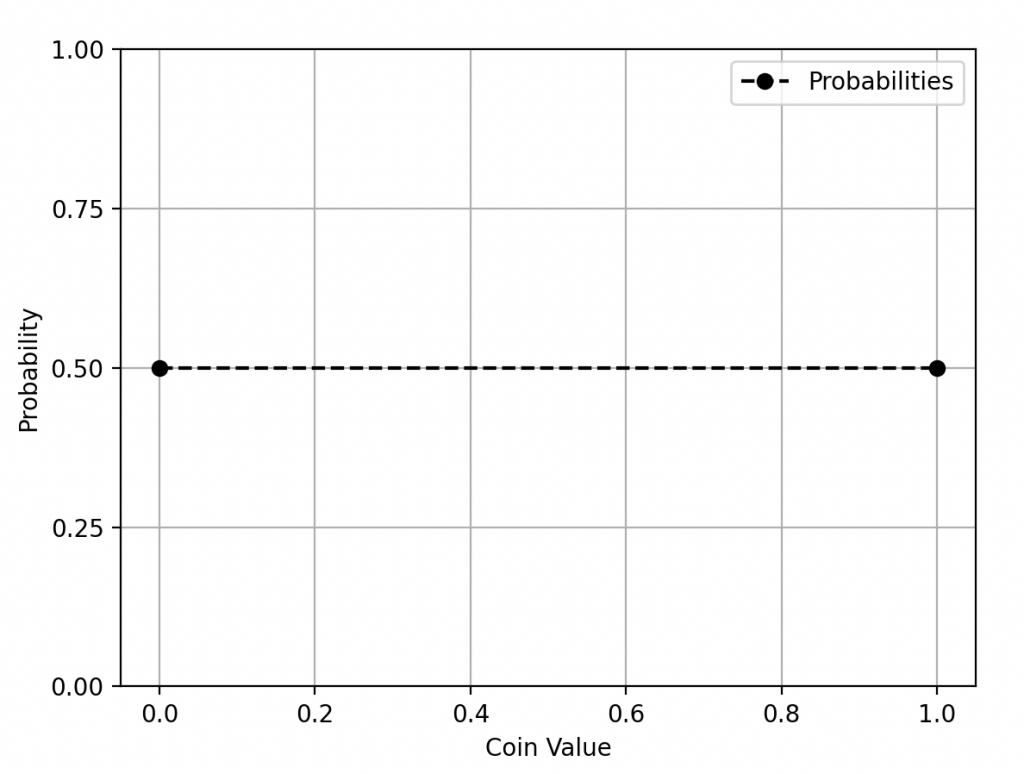
Distribución uniforme discreta con dos resultados (lanzamiento de moneda).

Para mis dados, es lo mismo. Un dado estándar tiene 6 caras, lo que corresponde a 6 modos, y si está equilibrado, decimos que todos son equiprobables.

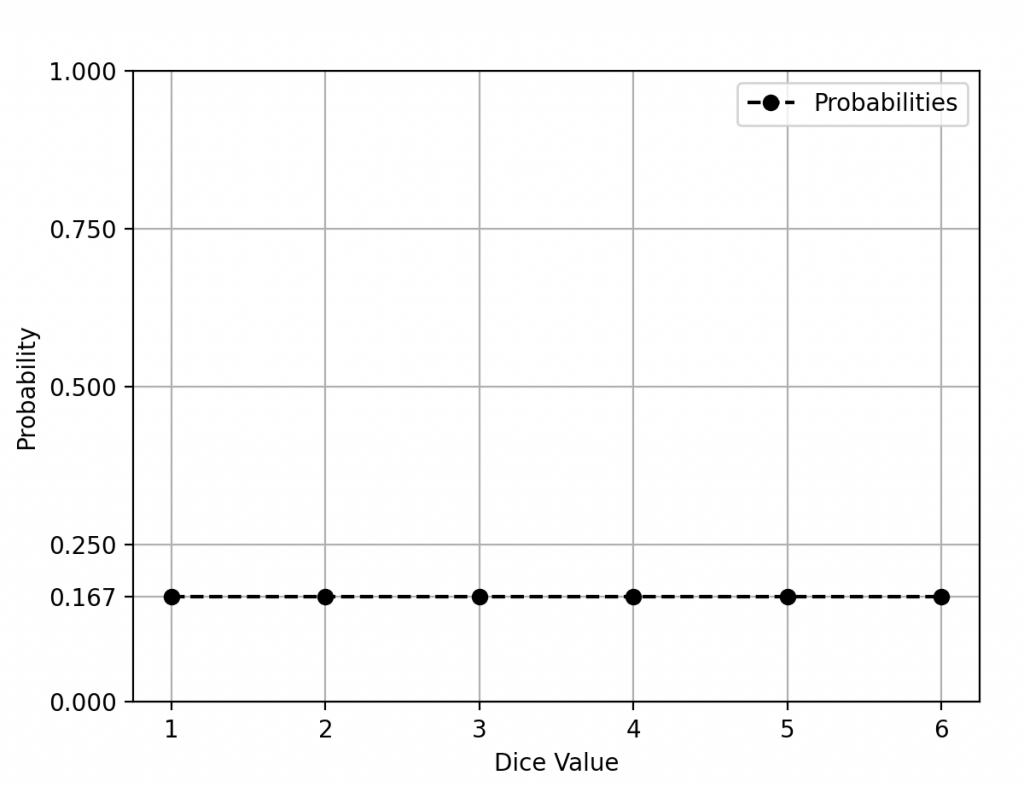
Distribución uniforme discreta con seis resultados (lanzamiento de un dado).
El Ladrón: (curioso) Muéstrame esa moneda, me gustaría examinarla de cerca para entender mejor el cara o cruz.
La Maga: (entregándole la moneda) Claro, aquí está la moneda. Está equilibrada, por lo que cada lado tiene una probabilidad igual de caer.
La Elfa: (levantando la mano) Espera, ¿qué podemos decir sobre el dado también?
La Maga: (sonriendo) Muchas cosas. Aquí están las principales características de estos dados:
Llamamos \(X\) a la variable aleatoria que sigue la distribución uniforme discreta (el lanzamiento de un dado).
• La esperanza: es como el promedio, y para un dado estándar, es \(\mathbb{E}(X)= \frac{6+1}{2}=3,5\)
• La mediana: es el valor del medio, también \(m(X)= \frac{6+1}{2}=3,5\) para un dado justo.
• La moda: aquí no hay una porque cada cara tiene la misma probabilidad de aparecer.
• La varianza: mide la dispersión de los resultados, y para un dado justo, es aproximadamente \(V(X)=\frac{6^{2}-1}{12}\approx2.91\)
• La asimetría es cero, y la curtosis…
El Ranger: (interrumpiendo) Perdón, pero ¿no es suficiente con las reglas? Ya entendimos lo básico.
La Maga: Bueno, hay algunas leyes más en este pergamino, la distribución triangular de probabilidad, la…
El Enano: (gruñón) ¡Por las barbas de nuestros antepasados, no vinimos aquí para una clase de matemáticas! Queremos tirar esos dados y jugar, no escuchar discursos interminables.
El Bárbaro: (golpeando la mesa) ¡Tiene razón! Todo esto está muy bien, pero queremos acción, no números.
El Ladrón: (examinando la moneda de cerca) Sí, estoy con ellos. ¿Podemos empezar a jugar ahora?
El Enano: ¡Devuélveme mi moneda!
La Maga: (tratando de mantener la calma) Está bien, está bien, veo que todos están impacientes. Pero antes de tirar los dados, déjame echar un último vistazo a esta nota al pie de la página. Quiero asegurarme de que estamos siguiendo todas las reglas.
La Maga comienza a leer rápidamente la nota al pie de la página, pero de repente se detiene.
La Maga: (sorprendida) Espera, ¡hay algo importante aquí que no había notado! Dice, «No voltees la moneda antes de jugar con los dados porque…»
Antes de que pueda terminar su frase, el Ladrón lanza la moneda de oro al aire para devolvérsela al Enano. Pero en lugar de caer en su mano, la moneda comienza a girar en el aire de manera misteriosa, emitiendo un brillo mágico.
El Enano: (sorprendido) ¡Por las barbas de nuestros antepasados, ¿qué está pasando?!
La moneda continúa girando en el aire, cada vez más rápido, y de repente desaparece por completo, dejando a todos desconcertados.
La Elfa: (asombrada) ¿Dónde fue la moneda?
La Maga: (impactada) No lo sé. Parece que los dados son más misteriosos de lo que pensaba.
El Bárbaro: (emocionado) Sea lo que sea, ¡parece divertido! ¡Vamos a lanzar los dados ahora!
El Enano: (molesto) ¿Dónde está mi moneda?
Fue una noche de juerga, discusiones acaloradas y alboroto en la antigua taberna. Los aventureros se detuvieron para relajarse después de un largo día de exploración y, como era su costumbre, se dejaron llevar por la emoción de la noche.
El Enano, que ya estaba de mal humor, decidió que todo era siempre culpa de la Elfa. Había tomado a la Elfa como chivo expiatorio, atribuyendo todas las desgracias del grupo a ella, repitiendo constantemente que «era culpa de la Elfa que todo saliera mal». Esta actitud deplorable solo empeoró a medida que avanzaba la noche.
Mientras jugaban a los dados y apostaban dinero, el Ladrón decidió animar la noche robando discretamente las bragas de una camarera. Fue un acto tan audaz como arriesgado, pero logró llevar a cabo esta hazaña con una destreza notable.
El Bárbaro, por otro lado, cedió a su impulsividad y golpeó al portero de la taberna en la entrada después de una pequeña discusión. El portero no perdió el tiempo y llamó a refuerzos, que rápidamente sometieron al bárbaro a base de golpes. Esto sumió al grupo en una situación aún más complicada.
El Ogre, siempre hambriento y curioso, decidió satisfacer su apetito tragándose una bola de billar. Esto provocó muchas risas entre los clientes de la taberna, pero también mucha preocupación por el bienestar del Ogre.
Finalmente, el Enano, completamente borracho, terminó vomitando su cerveza sobre el tabernero, desencadenando una pelea general entre los aventureros y los demás clientes.
El caos resultante solo podía llevar a una conclusión inevitable: todos los aventureros terminaron en el calabozo, donde tendrían que enfrentar nuevas aventuras para escapar de esta situación. Era el comienzo de una aventura que los llevaría mucho más lejos de lo que podrían haber imaginado en esa noche de excesos y desorden.
El Calabozo
El Ranger, conocido por su sabiduría (o al menos eso afirmaba), reunió al variopinto grupo de aventureros en un rincón oscuro de su sucia celda. El tenue destello de una antorcha titilante añadía una atmósfera pintoresca a su ya desagradable situación.
«Escúchenme, camaradas», comenzó el guardabosques con voz firme, aunque algo nerviosa. «Estamos en una situación desesperada, pero no somos cualquiera. Somos una tropa de élite, y no podemos resignarnos a quedarnos encerrados aquí como ratas comunes en una alcantarilla. Lo que necesitamos es un plan.»
Ante esto, la Elfa y el Enano empezaron a pelear como niños, llamándose mutuamente «chupadores de líquenes» y «comedores de rocas». El Enano, con la piel más gruesa que la Elfa (literalmente), respondió insultando las orejas puntiagudas del elfo y sugiriendo que volviera a tocar su flauta en el bosque.
El Bárbaro, que parecía increíblemente aburrido, interrumpió la disputa y decidió utilizar su fuerza hercúlea para intentar derribar la puerta. Desafortunadamente, había recibido un fuerte golpe en la cabeza durante el arresto y todavía estaba mareado por el impacto.
El Maestro de Juego le pidió que hiciera su tirada con desventaja, lo que significaba que lanzaría el dado dos veces y mantendría el resultado menos favorable. Además, la puerta estaba hecha de acero y diseñada para resistir los esfuerzos de los prisioneros que intentaban escapar de sus condenas.
Selecciona:
Number of dice = 1
Type of dice = 6
Lanza el dado dos veces y elige el resultado más pequeño.
Number of dice
Type of die:
Modifier
Result:

¿ Qué resultado obtuviste ?
Bibliografía
P. Barbé et M. Ledoux, Probabilité, Les Ulis, EDP Sciences, 2007.
P. Bogaert, Probabilités pour scientifiques et ingénieurs : Introduction au calcul des probabilités, Paris, Éditions De Boeck, 2006.
M. Lejeune, Statistique : la théorie et ses applications, Springer Science et Business Media, 2004.
F. Caravenna, P. Dai Pra et Q. Berger, Introduction aux probabilités : Modèles et applications : mathématiques, physique, informatique, sciences de l’ingénieur, biologie, Dunod, 1er septembre 2021.
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import norm
# Parameters for normal distributions
mean = 5 # Common mean for both distributions
variance1 = 10 # Variance for the first example
variance2 = 20 # Variance for the second example
# Generate data for the two distributions
x = np.linspace(-10, 20, 1000)
pdf1 = norm.pdf(x, loc=mean, scale=np.sqrt(variance1))
pdf2 = norm.pdf(x, loc=mean, scale=np.sqrt(variance2))
# Plot probability density functions with transparent fill color
plt.plot(x, pdf1, label=f'Variance={variance1}')
plt.fill_between(x, pdf1, alpha=0.3)
#plt.plot(x, pdf2, label=f'Variance={variance2}')
#plt.fill_between(x, pdf2, alpha=0.3)
# Calculate the mean for both cases (they should be equal)
mean1 = mean
mean2 = mean
# Draw vertical lines for the means
plt.axvline(x=mean1, color='r', linestyle='--', label=f'Mean')
plt.xlabel('Values')
plt.ylabel('Probability')
plt.legend()
plt.grid(True)
plt.show()
print(f"Mean (Var={variance1}): {mean1:.2f}")
print(f"Mean (Var={variance2}): {mean2:.2f}")
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import norm
# Parameters for normal distributions
mean = 5 # Common mean for both distributions
variance1 = 10 # Variance for the first example
variance2 = 20 # Variance for the second example
# Generate data for the two distributions
x = np.linspace(-10, 20, 1000)
pdf1 = norm.pdf(x, loc=mean, scale=np.sqrt(variance1))
pdf2 = norm.pdf(x, loc=mean, scale=np.sqrt(variance2))
# Plot probability density functions with transparent fill color
plt.plot(x, pdf1, label=f'Variance={variance1}')
plt.fill_between(x, pdf1, alpha=0.3)
plt.plot(x, pdf2, label=f'Variance={variance2}')
plt.fill_between(x, pdf2, alpha=0.3)
# Calculate the mean for both cases (they should be equal)
mean1 = mean
mean2 = mean
# Draw vertical lines for the means
plt.axvline(x=mean1, color='r', linestyle='--', label=f'Mean')
plt.xlabel('Values')
plt.ylabel('Probability')
plt.legend()
plt.grid(True)
plt.show()
print(f"Mean (Var={variance1}): {mean1:.2f}")
print(f"Mean (Var={variance2}): {mean2:.2f}")
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import skewnorm
# Parameters for the normal distribution
mean1 = 5
std_dev1 = 2
skewness1 = 0
# Parameters for the asymmetric normal distribution
mean2 = 5
std_dev2 = 2
skewness2 = 10 # Positive skewness (right-skewed)
# Create a range of x values
x = np.linspace(0, 10, 1000)
# Calculate the probability density functions (PDFs) for both distributions
pdf1 = skewnorm.pdf(x, skewness1, loc=mean1, scale=std_dev1)
pdf2 = skewnorm.pdf(x, skewness2, loc=mean2, scale=std_dev2)
# Plot the PDFs as curves
plt.plot(x, pdf1, label=f'Skewness={skewness1}')
plt.fill_between(x, pdf1, alpha=0.3)
plt.plot(x, pdf2, label=f'Skewness={skewness2}')
plt.fill_between(x, pdf2, alpha=0.3)
plt.xlabel('Values')
plt.ylabel('Probability')
plt.legend()
plt.grid(True)
plt.show()
import matplotlib.pyplot as plt
# Define possible values (coin faces)
values = [0, 1]
# Calculate uniform probabilities (each face has a 1/2 probability)
probabilities = [1/2] * 2
# Set the values to display on the y-axis
plt.yticks([0, 0.25, 1/2, 0.75, 1])
# Create the scatter plot
plt.plot(values, probabilities, marker='o', color='black', label='Probabilities', ls='--')
# Limit the y-axis scale from 0 to 1
plt.ylim(0, 1)
# Label the axes and add a title
plt.xlabel('Coin Value')
plt.ylabel('Probability')
# Display the plot
plt.grid(True)
plt.legend(loc='upper right')
plt.show()
import matplotlib.pyplot as plt
# Define possible values (dice faces)
values = [1, 2, 3, 4, 5, 6]
# Calculate uniform probabilities (each face has a 1/6 probability)
probabilities = [1/6] * 6
# Create the scatter plot
plt.plot(values, probabilities, marker='o', color='black', label='Probabilities', ls='--')
# Set the values to display on the y-axis
plt.yticks([0, 1/6, 0.25, 0.5, 0.75, 1])
# Label the axes and add a title
plt.xlabel('Dice Value')
plt.ylabel('Probability')
# Display the plot
plt.grid(True)
plt.legend(loc='upper right')
plt.show()

