Wall-E: El Compactador Terrestre de Basura
Episodio III
Por Jordan Moles el 2 de Diciembre, 2023

En calidad de robot fiel a su misión y entre algunas estimaciones de oro, Wall-E no olvida su tarea principal: clasificar los desechos. Fue durante sus expediciones a lugares remotos del planeta que descubrió el desafío definitivo que estimula su mente curiosa. Entre los objetos que recopila, Wall-E se encuentra con una variada colección de antiguos componentes electrónicos, algunos en buen estado que lleva de vuelta a la base, y otros defectuosos que almacena en un rincón.
Apasionado por tales objetos, se pone a desenroscar, arrancar y clasificar cuidadosamente cada componente en dos categorías distintas (clasificación binaria): por un lado, las piezas de metal valiosas que clasificará más adelante (clasificación multiclase) y, por otro lado, el plástico sin valor. La pregunta fundamental es: ¿cómo lleva a cabo tal misión?
Es muy recomendable haber leído los episodios I y II antes de continuar !
Los Nuevos Horizontes de Wall-E: La Clasificación
La épica de nuestro intrépido robot solitario, Wall-E, toma una nueva dimensión fascinante en su exploración del vasto reino de la clasificación. Después de dominar brillantemente el arte de la regresión en el episodio anterior (ver el artículo Wall-E el pequeño minero de oro), Wall-E emprende valientemente una nueva fase al adentrarse en la clasificación binaria entre metales preciosos y plásticos. Esta primera etapa preparatoria marca el comienzo de una búsqueda más compleja, donde Wall-E despliega con audacia sus habilidades de clasificación para navegar entre los diversos metales que pueblan su camino.
Basándose en sus éxitos iniciales, Wall-E decide ampliar su alcance al abordar la clasificación multiclase de los metales, convirtiendo así al algoritmo de K-Nearest Neighbors (KNN) en su aliado preferido. Este nuevo desafío exige de Wall-E una comprensión más profunda, ya que no solo debe distinguir entre dos categorías, sino también clasificar diferentes tipos de metales como bronce, oro y plata.
Esta nueva fase de su aventura marca la metamorfosis de Wall-E hacia horizontes de clasificación más amplios y sofisticados. Cada etapa de esta exploración le confiere una nueva dimensión a sus habilidades, preparando a Wall-E para enfrentar desafíos más complejos que la simple clasificación binaria. En este proceso, la selección del modelo resulta crucial para garantizar la precisión de sus predicciones. Wall-E comprende la importancia del proceso de validación cruzada y explora con minuciosidad las sutilezas de la ajuste de hiperparámetros, asegurando así la robustez y eficacia de su modelo.
El Elemento Clave: Siempre los Datos
En su exploración para descifrar la naturaleza de los componentes electrónicos, Wall-E se basa en la información almacenada durante su aprendizaje con sus creadores. Este enfoque busca construir un conjunto amplio y variado de muestras, alineándose con sus desafíos asociados a la regresión.
A la búsqueda de las muestras
Cada ejemplo \(k\) era un elemento con características específicas, como la densidad \(x^{(k)}\), la conductividad térmica \(x_2^{(k)}\), eléctrica \(x_3^{(k)}\), etc. Para ilustrar nuestro caso de manera simple, consideraremos únicamente y exclusivamente la variable densidad \(x^{(k)}\).
Así, para cada muestra \(k\), Wall-E registra si es un metal (etiquetado como \(y^{(k)}=1\)) o un plástico (etiquetado como \(y^{(k)}=0\)). Estas muestras y sus etiquetas forman su conjunto de datos de entrenamiento. Aquí tienes un ejemplo concreto de 5 muestras (de las 650 que ya conoce).
| Densidad | Tipo de Componente | |
|---|---|---|
| Muestra 1 | 2.165747 | Plástico |
| Muestra 2 | 7.151579 | Metal |
| Muestra 3 | 0.901240 | Plástico |
| Muestra 4 | 19.24357 | Metal |
| Muestra 5 | 12.54564 | Metal |
Las Fronteras de Decisión
La diferencia con el problema anterior es que aquí es necesario definir lo que llamamos una frontera de decisión. Expliquemos este concepto de manera simple. En lugar de mirar cada objeto individualmente, Wall-E decide dividir este espacio en diferentes regiones. Cada región estaría destinada a recibir un tipo específico de objeto, ya sea metal o plástico. Los límites de estas regiones definirán las fronteras, y aquí radica el corazón del problema de clasificación.
Cuando Wall-E dibuja estas fronteras, quiere asegurarse de que los objetos similares estén en la misma región. Esto significa que los objetos cercanos en densidad tienden a tener la misma etiqueta, ya sea metal o plástico. Idealmente, le gustaría que estos dos grupos estuvieran perfectamente separados, como si estuvieran en cajas distintas. Una simple línea podría ser suficiente.
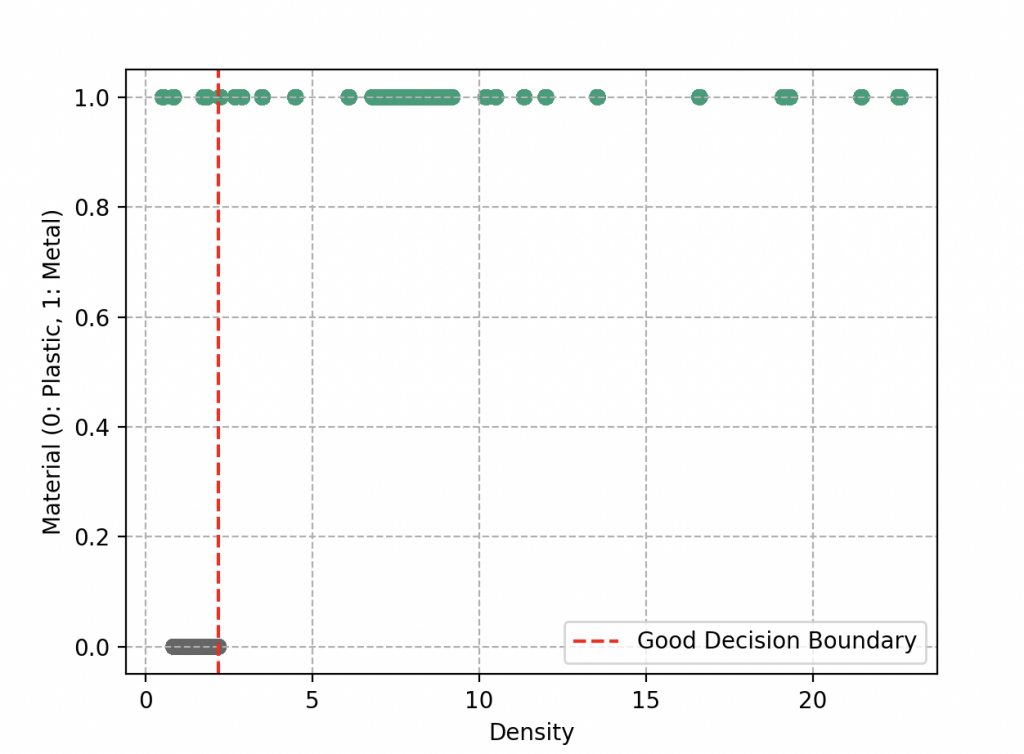

Sin embargo, la realidad no siempre es tan simple. A veces, hay objetos que están mal ubicados y terminan al otro lado de la línea. Esto ocurre cuando, en nuestro ejemplo, algunos plásticos tienen una densidad mayor que algunos metales (como el caucho y el litio que terminan a la izquierda de la frontera de decisión). Esto plantea un desafío para Wall-E. Ahora debe evaluar su trabajo en función de la calidad de la separación. Cuanto más clara sea la separación, mejor. Los objetos mal clasificados son como errores en su hoja de clasificación, y como de costumbre, quiere minimizar esos errores.
Wall-E también es consciente de que no debe complicarse la tarea dibujando fronteras zigzagueantes y complejas. Estas fronteras complicadas podrían capturar todos los objetos, pero también podrían llevarlo a una clasificación excesiva, donde cada objeto está en su propia región. Esto se llama sobreajuste (veremos eso en algunas secciones más adelante).
Creación del Modelo de Clasificación Binaria
Impulsado por el deseo de dar sentido a estos componentes electrónicos, Wall-E se embarca en la creación de un modelo de clasificación binaria. Este modelo tomará las características de un componente como entrada y proporcionará una predicción sobre su naturaleza como salida. Después de explorar diferentes enfoques, incluida la regresión lineal que sabe hacer con la función \(f(x)= ax+b\) (con los parámetros a y b) que no se ajusta en absoluto a los datos,


Wall-E opta por un modelo clásico de regresión logística, cuya función asociada (que oscila entre 0 y 1) se expresa de la siguiente manera:
\begin{align*}
\sigma(x)=\frac{1}{1+\exp{(-x)}}
\end{align*}
Se llama función logística o sigmoidal (debido a su forma en «S», ver a continuación).
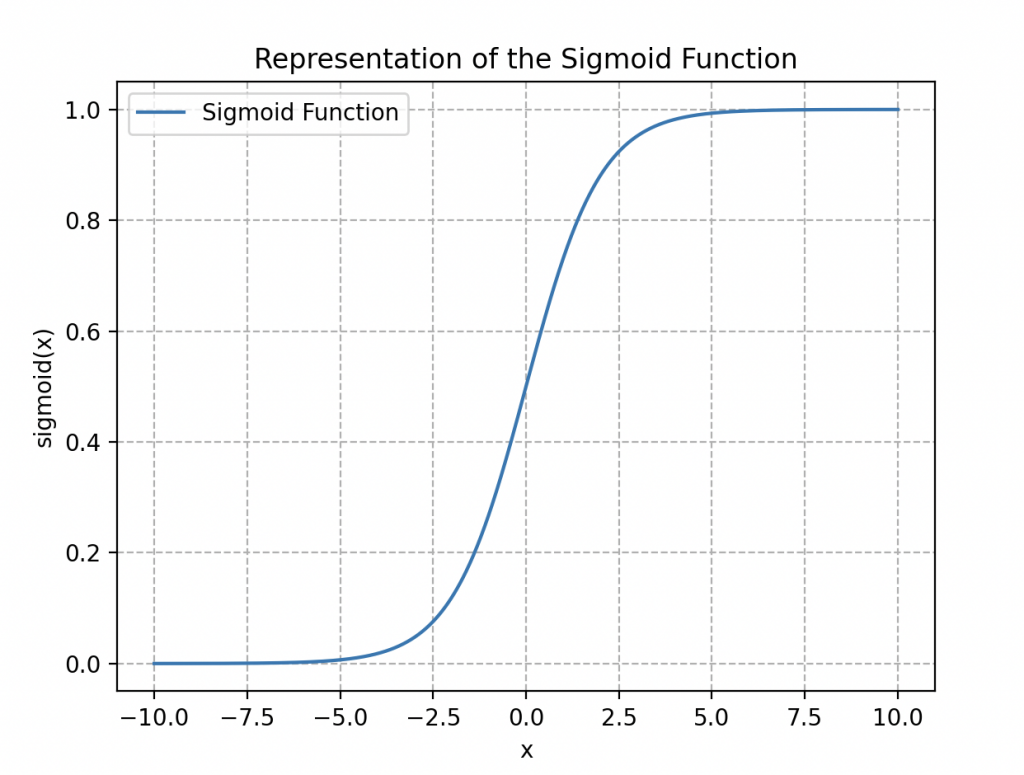
Aplicando esta función a nuestro conjunto de datos, obtenemos:
\begin{align*}
\sigma(z)=\frac{1}{1+\exp{(-z)}}
\end{align*}
donde \(z\) puede ser una función lineal como \(ax+b\) o polinómica, por ejemplo, \(ax^2 + bx + c\) (un polinomio de grado 2), con \(a\), \(b\) y \(c\) como parámetros a ajustar.
La gran ventaja de tal función es que podemos definir muy fácilmente una frontera de decisión fijando lo que llamamos un umbral de decisión.


Para entender formalmente por qué introducimos tal función, es necesario comprender que en el mundo de la clasificación, la idea para Wall-E es estimar la probabilidad de pertenencia de una muestra a cada categoría (metal o plástico), permitiendo así clasificar con confianza cada nueva observación en la categoría asociada a la probabilidad más alta. Así que cuando está cerca de la respuesta correcta, la probabilidad debe ser muy cercana a 1 y viceversa, si su respuesta se aleja de la realidad, entonces la probabilidad es casi nula.
El robot se inspira en esta noción fundamental cuando aborda el concepto de la función sigmoide. Entiende que esta función puede ser utilizada para transformar los resultados de la Regresión Logística en probabilidades. Como si aplicara una especie de filtro matemático a su evaluación, la función sigmoide asigna a cada componente una probabilidad de pertenecer a una categoría dada. Así que si esta probabilidad es mayor a 0.5, clasificamos el objeto en la categoría «metal»; si es menor a 0.5, será plástico.
Evaluación de Predicciones: La Función de Costo
Wall-E ha desarrollado su modelo, pero desea evaluar la precisión de sus predicciones. Para hacerlo, decide utilizar una de las funciones de costo de regresión, la MSE (consultar el artículo Wall-E el pequeño minero de oro), definida de la siguiente manera:
\begin{align*}
MSE(a, b) =\frac{1}{n} \sum_{k=1}^{n} \left(\sigma(x^{(k)})- y^{(k)}\right)^2.
\end{align*}
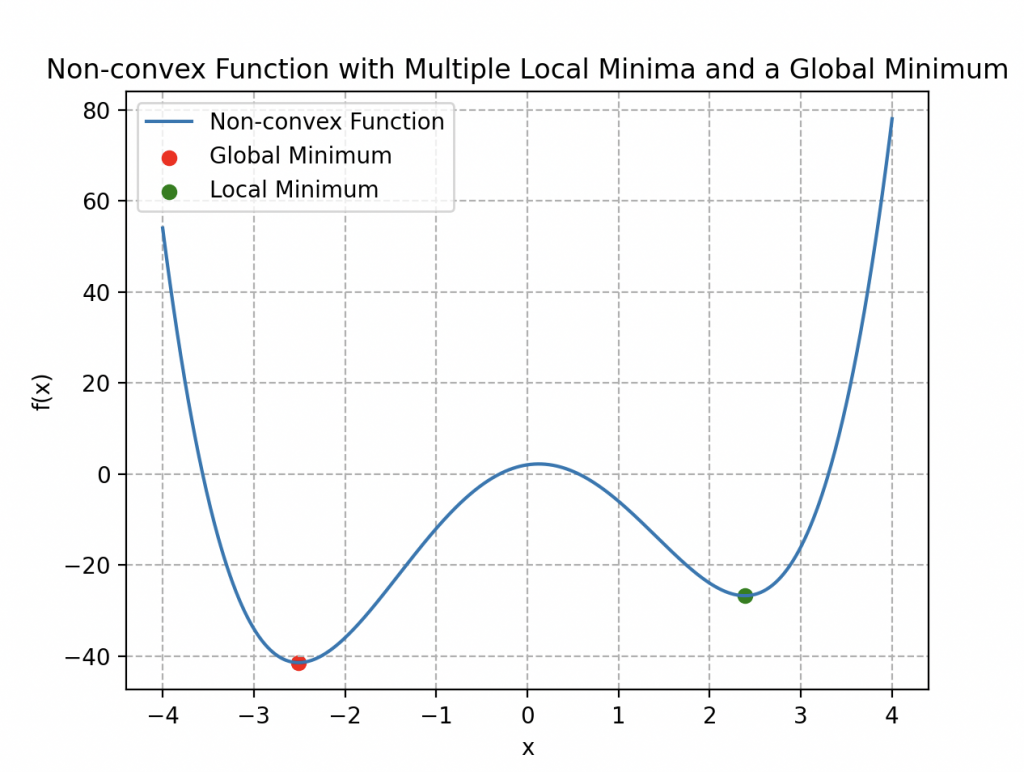
Sin embargo, se encuentra enfrentando un nuevo desafío considerable, como se ilustra en la imagen adjunta.
Esta función de costo no tiene un carácter convexo; de hecho, presenta varios mínimos locales. Esta característica hace que el algoritmo de descenso de gradiente sea menos eficiente, ya que, usando la analogía de un relieve montañoso, Wall-E corre el riesgo de quedar atrapado en un mínimo local que no necesariamente es el mínimo global de la curva.
Por lo tanto, introduce una nueva función de costo utilizando la función logaritmo:
\begin{align*}
L(a,b)=-\frac{1}{n}\sum_{k=1}^n\left[y^{(k)}\log{\left\{\sigma\left(ax^{(k)}+b\right)\right\}}+\left(1-y^{(k)}\right)\log{\left\{1-\sigma\left(ax^{(k)}+b\right)\right\}}\right]
\end{align*}
Esta función de costo compleja, aunque pueda parecer intimidante a primera vista, es en realidad una herramienta poderosa para evaluar el rendimiento del modelo. Permítame profundizar para explicar por qué Wall-E eligió esta función y cómo funciona.
El objetivo principal de una función de costo es medir cuán bien coinciden las predicciones del modelo con los valores reales. Cuanto más precisa sea esta correspondencia, menor será el valor de la función de costo. En el caso de la primera función de costo, Wall-E utilizó un enfoque más directo, donde comparaba las predicciones del modelo (obtenidas aplicando la función sigmoide a las entradas ponderadas) con los valores reales. Sin embargo, notó que este enfoque podría tener problemas durante la optimización.
La nueva función de costo introducida por Wall-E utiliza el logaritmo por una razón específica. Se compone de dos partes: una para los casos en que la etiqueta de clase es 1 (metal) y otra para los casos en que la etiqueta es 0 (plástico). Veamos en detalle cómo funcionan estas partes.
La primera parte de la función de costo, cuando una etiqueta es 1, está representada por el siguiente término:
\begin{align*}
-y^{(k)}\log{\left\{\sigma\left(x^{(k)}\right)\right\}}
\end{align*}
Aquí, \(y^{(k)}\) es el valor real de la clase para el ejemplo de entrenamiento \(k\) y \(x^{(k)}\) es la entrada correspondiente. Cuando \(y^{(k)}\) es igual a 1 (el ejemplo pertenece a la clase de metal) y la predicción \(\sigma\left(x^{(k)}\right)\) se acerca a 1, el valor de \(-\log{\left\{\sigma\left(x^{(k)}\right)\right\}}\) tiende hacia 0, contribuyendo así a un bajo valor de costo para ese ejemplo (el error es bajo porque la predicción es buena). En cambio, si la predicción se acerca a 0, el valor de \(-\log{\left\{\sigma\left(x^{(k)}\right)\right\}}\) se vuelve muy grande, lo que resulta en un aumento del costo.

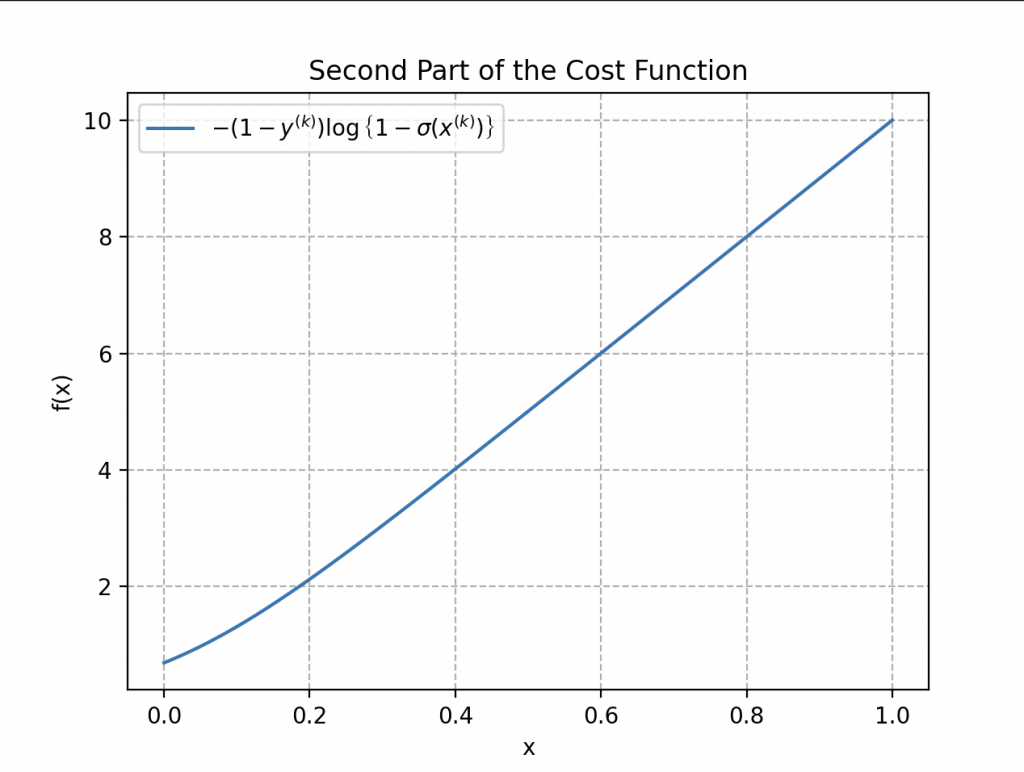
La segunda parte de la función de costo aborda los casos en los que la etiqueta es 0:
\begin{align*}
-\left(1-y^{(k)}\right)\log{\left\{1-\sigma\left(x^{(k)}\right)\right\}}
\end{align*}
Cuando \(y^{(k)}\) es igual a 0 (el ejemplo pertenece a la clase de plástico) y la predicción \(\sigma\left(x^{(k)}\right)\) está cerca de 0, el término \(\log{\left\{1-\sigma\left(x^{(k)}\right)\right\}}\) tiende hacia 0, contribuyendo a un costo bajo. Sin embargo, si la predicción se acerca a 1, \(\log{\left\{1-\sigma\left(x^{(k)}\right)\right\}}\) se vuelve grande, aumentando así el costo.
Así, cuando en la función de costo \(y^{(k)}\) es igual a 1, solo actúa la primera parte de la función, y si es igual a 0, entra en juego la otra.
La función de costo total es el promedio de estas dos partes, tomado sobre el conjunto de ejemplos de entrenamiento \(n\), para obtener una medida global del ajuste del modelo a los datos de entrenamiento. Esto permite evaluar los errores de predicción del modelo de una manera que penaliza más los errores importantes.
Ahora bien, ¿por qué elegir una función de costo tan compleja? El objetivo es permitir una optimización más eficiente del modelo. Esta función de costo tiene la ventaja de poseer una propiedad de convexidad, lo que significa que tiene un único mínimo global y no tiene mínimos locales. Esto facilita considerablemente el uso de algoritmos de optimización como el descenso de gradiente para ajustar los parámetros del modelo. Al evitar los mínimos locales, Wall-E puede tener más confianza en que la optimización conducirá a una solución de mejor calidad.
La Descenso de Gradiente, de Nuevo
¿Recuerdas el descenso de gradiente para la regresión? Hacemos exactamente lo mismo pero con la nueva función de costo. Algorítmicamente, tenemos:
• Nuestro robot calcula los gradientes de la función de costo en cada iteración, expresados matemáticamente de la siguiente manera:
\begin{align*}
\frac{\partial L(a, b)}{\partial a}&=\frac{1}{n}\sum_{k=1}^n\left(\sigma\left(ax^{(k)}+b\right)-y^{(k)}\right)x^{(k)},\\
\frac{\partial L(a, b)}{\partial b}&=\frac{1}{n}\sum_{k=1}^n\left(\sigma\left(ax^{(k)}+b\right)-y^{(k)}\right).
\end{align*}
Afortunadamente, tenemos una forma similar a la anterior.

• Actualiza los parámetros con los nuevos parámetros \(a^*\) y \(b^*\) de la siguiente manera:
\begin{align*}
a^*&=a-\delta\times\frac{\partial L(a, b)}{\partial a}\\
b^*&=b- \delta\times\frac{\partial L(a, b)}{\partial b}
\end{align*}
• Repite el proceso hasta encontrar el mínimo de la función de costo.
El Poder del Pequeño Clasificador de Residuos
Así es como nos encontramos en el corazón de su misión de clasificación de residuos. Las tablas de datos se extienden ante él, decoradas con vectores y matrices que revelan los misterios de las muestras de componentes electrónicos. Encontramos el vector \(\mathbf{Y}\) compuesto por n elementos correspondientes a las n muestras de componentes electrónicos.
Junto a este vector, aparece una matriz \(\mathbf{X}\) compuesta por n filas y m+1 columnas. Esta matriz contiene las características precisas de cada muestra, aquí solo una característica de densidad y su columna de sesgo.
Recuerda que, de manera general, tenemos:
También encontramos un vector «parámetro» \(\mathbf{P}\) que reúne los parámetros del modelo \(a\) y \(b\) que utilizaremos para minimizar la función de costo.
Esta tarea de clasificación se puede comparar con un problema que ya resolvió, donde estimaba el precio del oro en función de su pureza. Para resolver este nuevo desafío, Wall-E utiliza un enfoque similar basado en la función sigmoide, traduciendo sus cálculos a forma matricial.
• La recolección se realiza mostrando los datos en una matriz: cada muestra, con sus características de densidad y su clase, encuentra su lugar en esta matriz.
• La Creación del Modelo es el proceso donde Wall-E define los parámetros mostrados en la columna \(\mathbf{P}\) tomados al azar, que se utilizan para establecer la relación entre la densidad y la naturaleza del componente mediante la sigmoide en forma matricial un tanto compleja (donde se aplica la sigmoide a cada coordenada):
\begin{equation*}
\mathbf{\sigma(X\times P)}=\left[
\begin{array}{c}
\frac{1}{1+\exp{(-ax^{(1)}+b)}}\\
\frac{1}{1+\exp{(-ax^{(2)}+b)}} \\
\vdots \\
\frac{1}{1+\exp{(-ax^{(n)}+b)}} \\
\end{array}
\right].
\end{equation*}
• La Función de Costo se redefine de la siguiente manera:
\begin{align*}
L(\mathbf{P})=-\frac{1}{n}\left[\mathbf{Y\cdot\log{\left\{\sigma(X\times P)\right\}}}+\mathbf{(1-Y)\cdot\log{\left\{1-\sigma(X\times P)\right\}}}\right].
\end{align*}
donde \(\cdot\) es el producto escalar.
• Encontrar el mínimo implica calcular el gradiente:
\begin{align*}
\frac{\partial }{\partial \mathbf{P}} L(\mathbf{P})=\frac{1}{n}\mathbf{X\cdot\left(\sigma(X\times P)-Y\right)}
\end{align*}
y aplicar iterativamente el descenso de gradiente para actualizar el parámetro \(\textbf{P}\):
\begin{align*}
\mathbf{P^*}=\mathbf{P}-\delta \frac{\partial }{\partial \mathbf{P}}L(\mathbf{P})
\end{align*}
donde \(\mathbf{P^*}\) es el nuevo parámetro.
Wall-E, gracias a una ejecución rigurosa de todos los pasos necesarios, ha perfeccionado su capacidad para clasificar el plástico del metal. ¡Ahora está listo para clasificar cada material que le proporcionen! Descubre la curva final que ha obtenido.
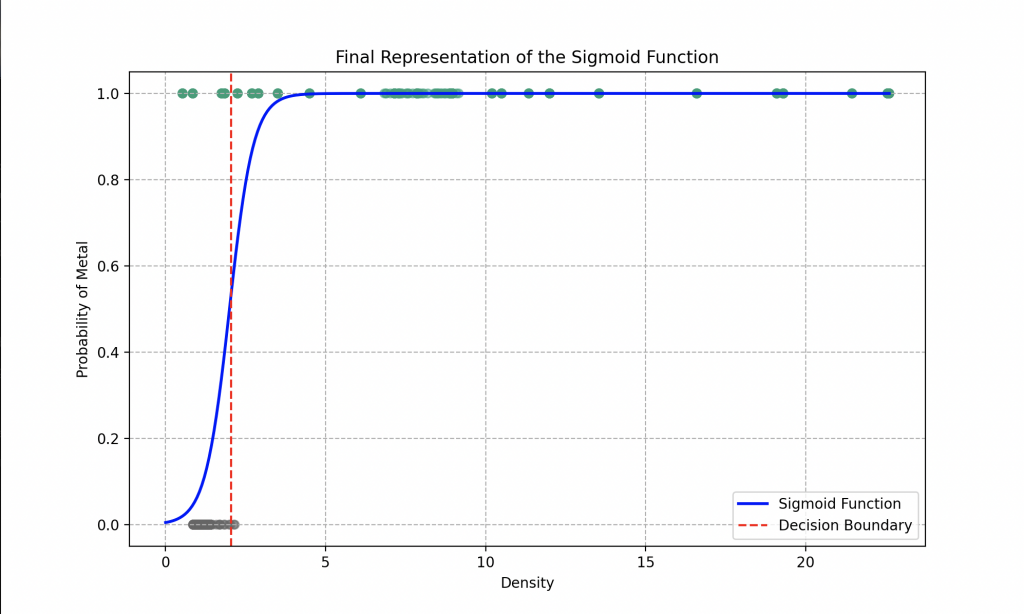
Nuestro robot favorito ha optado por utilizar una función lineal en su regresión logística. Los parámetros óptimos que determinó después de la descenso de gradiente son \(a = 16.85\) y \(b = 9.71\).
El análisis del gráfico revela que si el robot encuentra un objeto en la naturaleza con una densidad de 1.5, por ejemplo, puede afirmar con una precisión de aproximadamente 80% que se trata de un plástico. Para una densidad de 0.5, puede identificar el material como plástico con una precisión del 98%, mientras que una densidad de 4 lo lleva a concluir que es metal con una precisión del 99%.
A través de su modelo de regresión logística, el robot puede, en términos generales, determinar con una precisión del 93% si el material proporcionado es metal o plástico. Sin embargo, para refinar aún más sus predicciones, sería beneficioso explorar características más complejas en la función sigmoide, como el uso de polinomios con un mayor número de parámetros para ajustar, por ejemplo.
Además, el modelo podría mejorarse considerablemente al adoptar algoritmos más sofisticados que la regresión logística. Enfoques como Random Forest, Support Vector Machines (SVM) o incluso k vecinos más cercanos (que exploraremos en las próximas secciones) podrían ofrecer un rendimiento optimizado.
Otra estrategia para fortalecer la capacidad del modelo sería proporcionarle un conjunto más amplio de características, como la conductividad eléctrica, térmica, etc., o aumentar la cantidad de datos. Al enriquecer así el conjunto de datos, el robot podría mejorar su comprensión de las sutilezas existentes entre diferentes tipos de materiales, lo que conduciría a clasificaciones más precisas y robustas.
Más allá de la Clasificación de Residuos: Determinación de Tipos de Metales
Explorando más profundamente en el campo de la clasificación de metales, Wall-E se enfrenta a un desafío más complejo: determinar el tipo específico de metal entre una variedad de aleaciones que incluyen bronce, oro, plata, y muchos otros.
Para abordar este desafío, la herramienta preferida de Wall-E se convierte en el algoritmo de los K vecinos más cercanos (KNN), también conocido como K-nearest neighbor.
Es importante destacar que creamos el conjunto de datos desde cero seleccionando las características de las muestras de manera aleatoria, pero lo suficientemente cerca de los valores fijos de densidad y conductividad eléctrica de los metales puros (una medida de la capacidad de un metal para conducir electricidad). Aquí está la lista de todos los metales puros que hemos registrado para Wall-E con sus características respectivas.
| Tipo de Metal | Conductividad Eléctrica (en Giga S/m) | Densidad |
|---|---|---|
| Acero | 1.5 | 7.500 - 8.100 |
| Aluminio | 37.7 | 2.700 |
| Plata | 63 | 10.500 |
| Berilio | 31.3 | 1.848 |
| Bronce | 7.4 | 8.400 - 9.200 |
| Carbono (grafito) | 61 | 2.250 |
| Cobre | 59.6 | 8.960 |
| Estaño | 9.17 | 7.290 |
| Hierro | 9.93 | 7.860 |
| Iridio | 19.7 | 22.560 |
| Litio | 10.8 | 5.30 |
| Magnesio | 22.6 | 1.750 |
| Mercurio | 1.04 | 13.545 |
| Molibdeno | 18.7 | 10.200 |
| Níquel | 14.3 | 8.900 |
| Oro | 45.2 | 19.300 |
| Osmio | 10.9 | 22.610 |
| Paladio | 9.5 | 12.000 |
| Platino | 9.66 | 21.450 |
| Plomo | 4.81 | 11.350 |
| Potasio | 13.9 | 0.850 |
| Tantalio | 7.61 | 16.600 |
| Titanio | 2.34 | 4.500 |
| Tungsteno | 8.9 | 19.300 |
| Uranio | 3.8 | 19.100 |
| Vanadio | 4.89 | 6.100 |
| Zinc | 16.6 | 7.150 |
Esto simula aleaciones metálicas, donde cada aleación se considera compuesta por un metal puro a determinar e impurezas que modifican ligeramente sus características. La base de datos de Wall-E consta de 300 muestras para cada tipo de aleación metálica. Aquí hay cinco, cada una caracterizada por sus propiedades distintivas.
| Tipo de Metal | Conductividad Eléctrica (En Giga S/m) | Densidad |
|---|---|---|
| Acero | 2.7093 | 7.7446 |
| Vanadio | 5.8000 | 7.5000 |
| Hierro | 9.2600 | 8.4000 |
| Oro | 43.000 | 18.500 |
| Bronce | 7.51320 | 8.7000 |
Por lo tanto, el objetivo de Wall-E será clasificar cada muestra metálica que encuentre según su densidad y conductividad eléctrica en una categoría de metales puros.
Contraste con la Clasificación Binaria y Complejidades de la Clasificación Multiclase
Wall-E, después de dominar la clasificación binaria para distinguir entre metales preciosos y plásticos, se da cuenta de que el siguiente paso, la clasificación multiclase, representa un desafío más complejo. Mientras que la clasificación binaria simplemente divide los objetos en dos categorías distintas, como metal o plástico, Wall-E ahora debe diferenciar entre tipos específicos. La simplicidad de una frontera de decisión como una línea, utilizada en la clasificación binaria, ya no es suficiente.
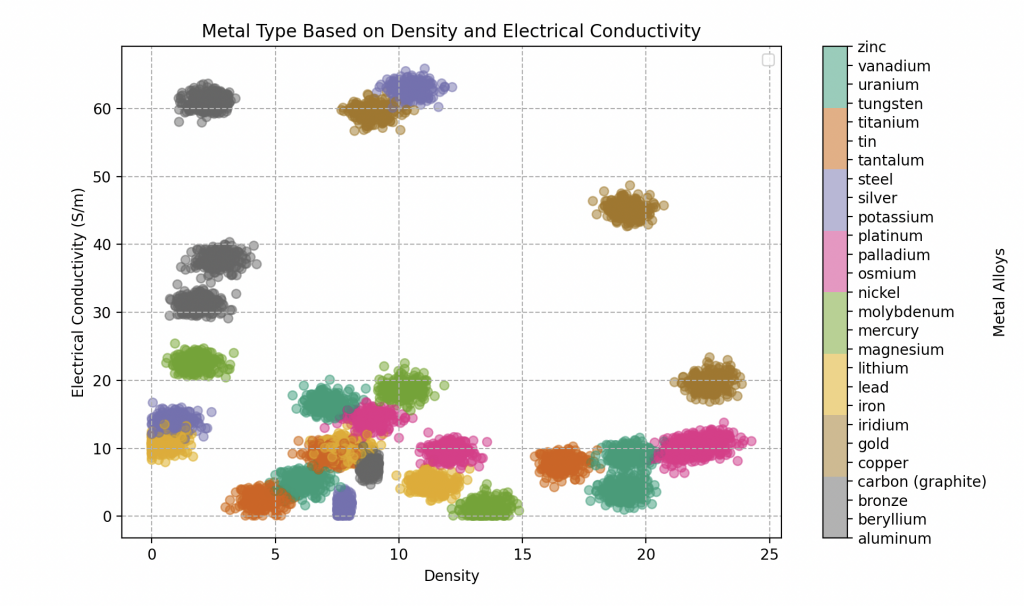
En este nuevo territorio, Wall-E debe navegar en un espacio característico complejo donde los metales pueden superponerse. Esta complejidad, por lo tanto, requiere un enfoque más refinado, y es aquí donde Wall-E recurre a un método que tiene en cuenta las sutilezas de las relaciones entre los metales.
El Poder de la Proximidad: K Nearest Neighbors
En esta búsqueda, Wall-E recurre al algoritmo KNN, o K vecinos más cercanos, que es un método de clasificación basado en el concepto fundamental de proximidad en el espacio de características.
La idea esencial detrás de KNN consiste en agrupar objetos similares en el espacio de características. En nuestro contexto, esto significa que si un trozo de bronce comparte características similares con otros trozos de bronce, estos objetos estarán cercanos entre sí en este espacio multidimensional. Wall-E aprovecha hábilmente esta noción para asignar a cada trozo de metal una etiqueta correspondiente a su tipo.
Su proceso de funcionamiento es bastante intuitivo. Cuando se debe clasificar un nuevo trozo de metal, Wall-E mide sus características específicas, como la densidad, la conductividad eléctrica, etc., posicionándolo así en el espacio de características. Luego, el algoritmo identifica los k vecinos más cercanos a este nuevo trozo en este espacio. Estos vecinos son los trozos de metal que comparten características similares.
Una vez identificados los vecinos, KNN asigna al nuevo trozo el tipo de metal que recibe la mayoría de votos entre estos vecinos cercanos. Es como si cada vecino votara por la categoría a la que pertenece, y el tipo de metal con el mayor número de votos se asigna al nuevo trozo.

Esta aproximación flexible y basada en la proximidad permite que Wall-E clasifique con precisión los metales, incluso sin tener una comprensión profunda de las características específicas de cada tipo. Así, KNN se convierte en un aliado eficaz en la búsqueda de Wall-E para determinar el tipo de metal, aprovechando el poder de la cercanía en el espacio de características.
Proceso de Clasificación Metálica: los Vecinos en Acción
Wall-E busca en su base de datos relativamente extensa, que incluye diversos tipos de metales y aleaciones, cada uno asociado con características específicas como la conductividad eléctrica, la densidad y otras propiedades únicas. Estas características constituyen las dimensiones del espacio de características donde cada metal está representado. Desafortunadamente, no ha tenido tiempo de medir todas las propiedades de cada metal y, por lo tanto, debe conformarse solo con la densidad y la conductividad eléctrica.
Cuando aparece un nuevo trozo de metal, Wall-E activa el algoritmo KNN para determinar su tipo. El proceso se desarrolla de la siguiente manera:
• Medición de Características: Wall-E mide las características del nuevo trozo de metal, colocándolo así en el espacio de características.
• Identificación de Vecinos Cercanos: KNN identifica los k vecinos más cercanos al nuevo trozo en este espacio. Estos vecinos son los trozos de metal que comparten características similares.
• Mayoría de Votos: Al examinar los tipos de metal de los vecinos, Wall-E asigna al nuevo trozo el tipo que recibe la mayoría de votos entre los vecinos cercanos, es decir, el tipo de metal mayoritario.

Este proceso de vecindario y votación permite que Wall-E clasifique con precisión el nuevo trozo de metal, incluso sin un conocimiento profundo de las características específicas de cada tipo. ¡Lo logra de manera excepcional!
En una misión en busca de artefactos electrónicos a bordo de su nave espacial, nuestro intrépido explorador se embarca en un proceso meticuloso de desmontaje y medición, examinando la densidad y la conductividad eléctrica de cada componente desconocido. Gracias al algoritmo KNN, finamente ajustado con un parámetro k óptimo de 20 vecinos, elegido después de pruebas exhaustivas (ver la próxima sección), puede afirmar con una seguridad cercana al 95% su capacidad para identificar cualquier aleación metálica.
Un logro tecnológico que atestigua la precisión de sus clasificaciones.

El primer objeto sometido a su análisis revela una densidad de 18.5 y una conductividad eléctrica de 43 gigasiemens por metro. Nuestro explorador se llena de entusiasmo al darse cuenta de que ha encontrado oro.
Mejor aún, su certeza alcanza una puntuación impresionante del 100% (como sugiere claramente el gráfico adjunto).
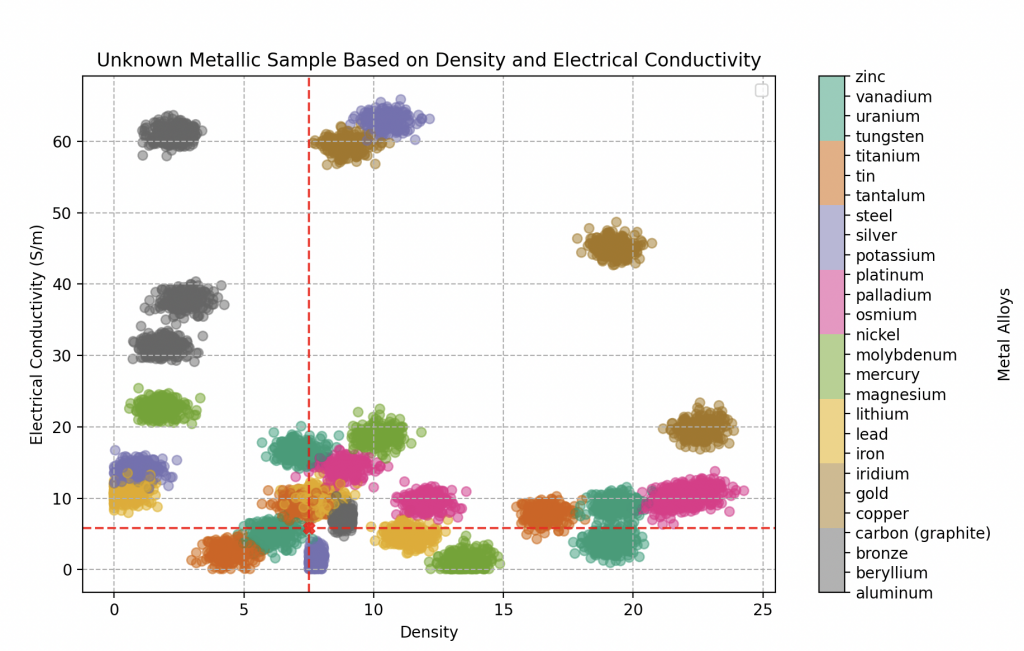
El segundo componente que captura su atención es una placa metálica grisácea, con rastros de óxido. Las mediciones revelan una densidad de 8.4 y una conductividad eléctrica de 9.26 gigasiemens por metro.
La aplicación de su algoritmo KNN sugiere una alta probabilidad de una aleación de hierro, con una certeza del 70%. Sin embargo, persiste cierta incertidumbre, llevándolo a considerar también posibilidades como bronce (20% probable) o estaño (10% probable). El misterio persiste, revelando la complejidad de los elementos metálicos descubiertos.
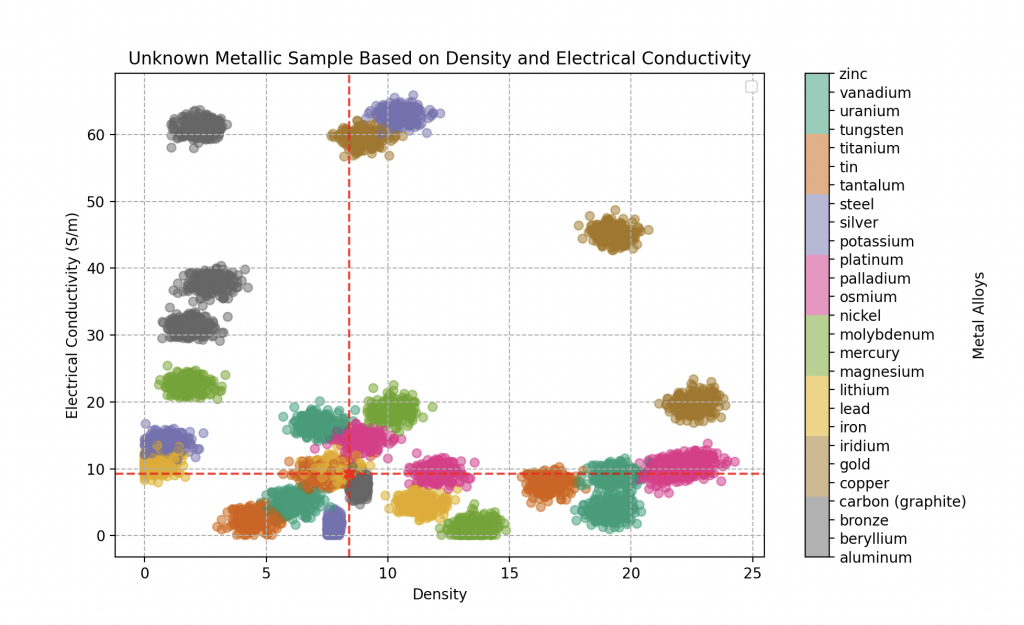
Finalmente, el último componente, con una densidad de 7.5 y una conductividad eléctrica de 5.8 gigasiemens por metro, revela una composición metálica compleja.
El análisis detallado del algoritmo KNN indica una predominancia de un metal particularmente raro: el vanadio, probable en aproximadamente un 70%. Le sigue de cerca el estaño con un 25%, y finalmente, el hierro con un 5%.
Wall-E asimila rápidamente las sutilezas del proceso de análisis, especialmente la complejidad que surge cuando los metales se superponen en el gráfico. Reconoce que predecir con una certeza absoluta del 100% puede volverse complicado en estas situaciones. Sin embargo, a pesar de estos desafíos, los resultados obtenidos por el algoritmo KNN siguen siendo excepcionales.
El rendimiento del algoritmo en la clasificación de metales, incluso en escenarios donde las características se superponen, testimonia su eficacia y robustez. Así, Wall-E puede aprovechar esta técnica poderosa para explorar y clasificar diversos componentes metálicos con una confianza aumentada.
El Arte de la Selección del Modelo
En el corazón de su búsqueda de clasificación de componentes electrónicos (clasificación) e incluso de la estimación del precio del oro (regresión), el pequeño robot se da cuenta de la necesidad de navegar con precaución.
Exploración de Nuevos Horizontes: Entrenamiento y Prueba
Rápidamente comprende la importancia de nunca evaluar su modelo en los mismos datos que se utilizaron para su entrenamiento.
Para ilustrar este punto, imaginemos que Wall-E enseña a jóvenes robots a analizar meteoritos, dando varios cursos y proporcionando ejercicios prácticos para su entrenamiento con el objetivo de evaluarlos al final de su ciclo escolar.
Sin embargo, Wall-E es consciente de que si controla el rendimiento de sus aprendices en los mismos meteoritos utilizados durante su clase, esto haría la tarea demasiado fácil. Los robots simplemente se limitarían a reconocer características específicas ya encontradas, sin una comprensión real.

Para evitar este sesgo, Wall-E implementa un enfoque ingenioso: divide el conjunto de ejercicios (su conjunto de datos) en dos partes distintas, creando así el conjunto de entrenamiento (train set) y el conjunto de prueba (test set).
El conjunto de entrenamiento, que generalmente representa el 80 por ciento de los datos, está destinado al entrenamiento del modelo; Wall-E guía a los jóvenes robots a través de clases y ejercicios utilizando estos datos. Por otro lado, el conjunto de prueba, que consta del 20 por ciento de los datos, se reserva para la evaluación final del modelo.
Así, cuando Wall-E prueba los conocimientos adquiridos por los robots en nuevos meteoritos, se asegura de que puedan aplicar sus habilidades a situaciones inéditas, evitando simplemente la memorización de los datos de entrenamiento. Este proceso garantiza que el modelo sea capaz de generalizar y proporcionar predicciones precisas incluso en datos no vistos anteriormente.
Elevación hacia la Excelencia: Validación del Modelo
Firme de sus habilidades en entrenamiento y evaluación de modelos de aprendizaje automático, Wall-E, como experimentado científico de datos, se embarca ahora en mejorar la precisión de su modelo. Para lograrlo, debe ajustar los hiperparámetros del modelo, una tarea similar a afinar los ajustes de una antena de radio para una recepción óptima. Por ejemplo, en el caso de su modelo anterior, ajustar el número de vecinos de su clasificador KNN.
Sin embargo, Wall-E es consciente de las trampas que podrían surgir si optimiza el rendimiento de su modelo en el conjunto de prueba. Esto haría que los datos del conjunto de prueba fueran inutilizables para la evaluación final. Para evitarlo, Wall-E introduce una tercera sección en su conjunto de datos: el conjunto de validación. Esta sección le permite explorar las configuraciones del modelo que ofrecen el mejor rendimiento, al tiempo que preserva los datos del conjunto de prueba para una evaluación imparcial.
Al comparar diferentes modelos, como los clasificadores KNN con 2, 3, 20 o incluso 100 vecinos, Wall-E sigue una metodología rigurosa. Comienza entrenando estos modelos en el conjunto de entrenamiento. Luego, selecciona el modelo que ofrece el mejor rendimiento en el conjunto de validación. Finalmente, para estimar el rendimiento real en situaciones del mundo real, evalúa este modelo seleccionado en el conjunto de prueba.
Wall-E ilustra estas elecciones trazando dos curvas esenciales: el rendimiento en el conjunto de entrenamiento y el rendimiento en el conjunto de validación.
Las curvas aquí representan las puntuaciones de entrenamiento y validación en función de los diferentes valores del parámetro explorado, como el número de vecinos en el caso de los clasificadores KNN.
Esta visualización permite detectar tendencias cruciales, como el sobreajuste (overfitting) o el subajuste (underfitting) del modelo según los valores del parámetro.
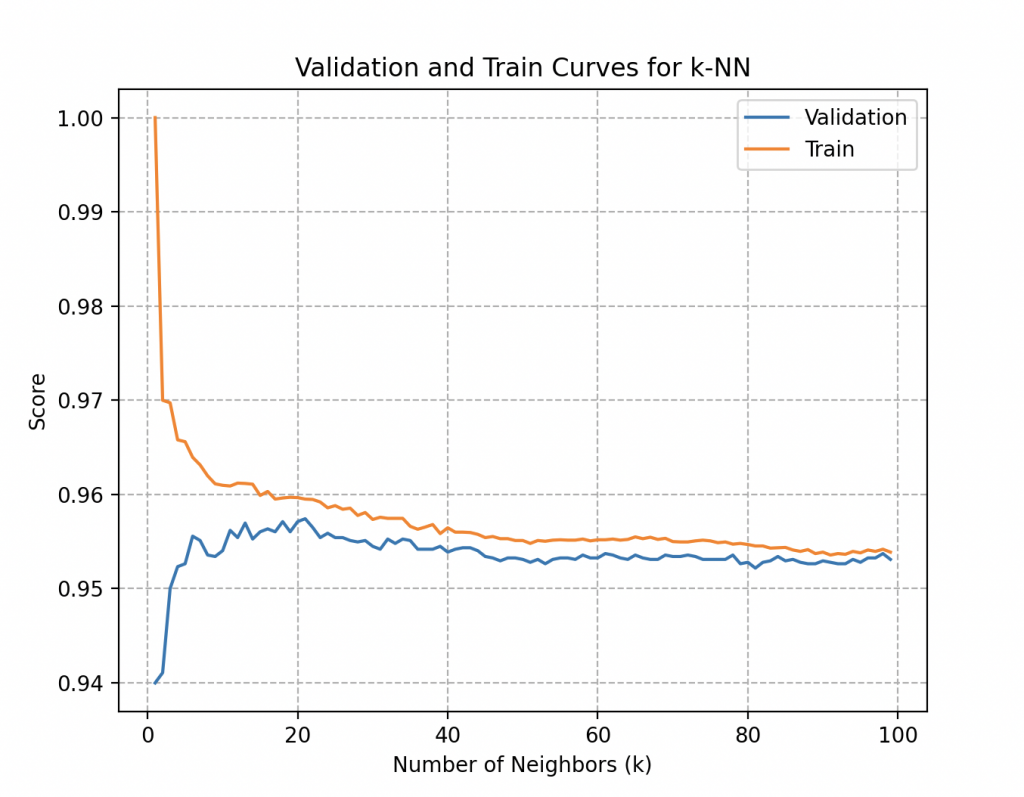
Más específicamente, la curva de validación para el número de vecinos (k) en el KNN proporciona respuestas a preguntas clave.
– Sobreajuste: La diferencia significativa entre la puntuación de entrenamiento y la puntuación de validación puede indicar sobreajuste, lo que significa que el modelo es demasiado complejo y pierde generalización. El sobreajuste es un comportamiento indeseable en el aprendizaje automático que ocurre cuando el modelo de aprendizaje hace predicciones precisas para los datos de entrenamiento, pero no para nuevos datos.
– Subajuste: Por otro lado, cuando un modelo no ha aprendido bien los patrones en los datos de entrenamiento y no logra generalizar correctamente a nuevos datos, se habla de subaprendizaje. Un modelo de subaprendizaje tiene un rendimiento deficiente en los datos de entrenamiento y conduce a predicciones no confiables.
– Sensibilidad a la Elección del Parámetro: Observar las variaciones en el rendimiento del modelo con diferentes valores del número de vecinos permite a Wall-E elegir un valor óptimo de k, maximizando así el rendimiento del modelo.
Adoptando este enfoque metódico, Wall-E se asegura de tomar decisiones informadas para la configuración óptima de su modelo, evitando así las trampas del sobreajuste o el subajuste y garantizando un rendimiento óptimo en situaciones del mundo real.
En su caso, ambas curvas alcanzan rápidamente una precisión del 95,7% a partir de alrededor de 20 a 25 vecinos y se estancan alrededor de ese valor a medida que aumenta el número de vecinos. Un análisis más profundo de las curvas (que no detallaremos aquí) indicaría que la cantidad óptima de vecinos es 20.
Aunque tiene una comprensión profunda del proceso, Wall-E sabe que queda un último detalle crucial: ¿cómo garantizar que la partición del conjunto de datos sea la mejor? Encuentra la solución en la validación cruzada.
La Danza de los Modelos: Validación Cruzada
Wall-E utiliza una metodología de validación cruzada ingeniosa para fortalecer la robustez de la selección de su modelo. En particular, adopta el método K-fold, donde el conjunto de datos se divide en K partes (en este caso, 5 partes). Durante el entrenamiento, el modelo de Wall-E se entrena sistemáticamente en K-1 de estas particiones y se valida en la partición restante, repitiendo este proceso K veces. Esto garantiza una evaluación más confiable y estable del rendimiento del modelo, asegurándose de que ninguna partición en particular influya excesivamente en los resultados.
Además, Wall-E también aprovecha el Stratified K-fold, una variante inteligente del K-fold, que tiene en cuenta la distribución de las clases en el conjunto de datos. Este enfoque garantiza que cada fold mantenga una representación proporcional de todas las clases, lo cual es crucial cuando las clases no están distribuidas de manera equitativa. Así, Wall-E asegura una selección de modelo robusta, resistente a las variaciones en la división de los datos, al tiempo que tiene en cuenta la distribución de las clases para una evaluación aún más precisa.
Obviamente, existen otros métodos de partición que se adaptan de manera más o menos eficaz según los datos disponibles, los cuales discutiremos en un próximo artículo.
Las Olas del Aprendizaje: Curvas de Aprendizaje
Curioso por determinar si su modelo puede beneficiarse de una mejora mediante la adición de datos adicionales, Wall-E se embarca en una exploración más profunda al examinar las curvas de aprendizaje.
Estas curvas ofrecen una representación visual de la evolución del rendimiento del modelo en función de la cantidad de datos de entrenamiento proporcionados. Aunque la adición de datos puede conducir inicialmente a una mejora en el rendimiento, Wall-E tiene la perspicacia de reconocer que estos beneficios eventualmente alcanzan un umbral. Comprender el momento en que el modelo alcanza sus límites se convierte así en una sabiduría invaluable, permitiendo un uso prudente del tiempo y los recursos.

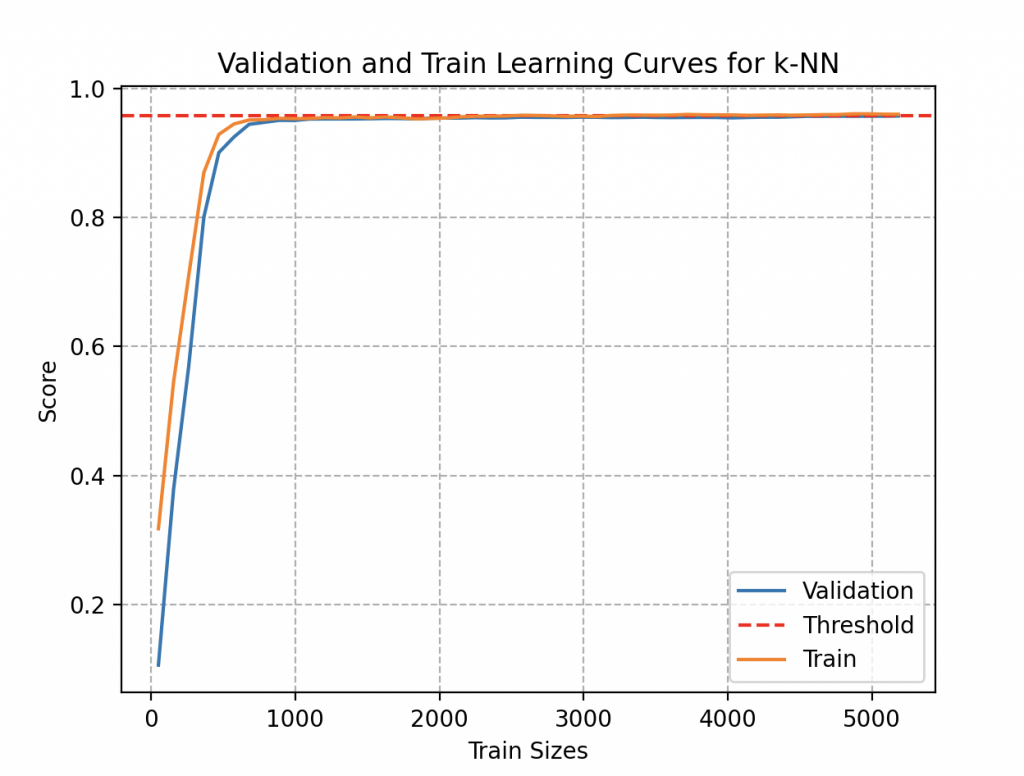
Al examinar esta curva, nota que se podría haber obtenido una estimación lo suficientemente precisa utilizando menos de 1000 muestras de metales, aproximadamente 37 aleaciones de cada tipo. Incluso acumulando 300 muestras de metales para cada tipo (300 veces 27, es decir, 8100 objetos), observa que esto apenas aporta una mejora significativa a su modelo (su precisión se estanca en 95,7%). ¡Afortunadamente, él recopila datos por placer!
Así, Wall-E baila con agilidad al ritmo de las olas del aprendizaje, navegando con destreza en el complejo paisaje de la selección del modelo. Al dominar las sutilezas de las curvas de aprendizaje, Wall-E asegura aprovechar al máximo su proceso de mejora del modelo.
El Fin de una Trilogía, el Comienzo de una Era Tecnológica
Esta última entrega marca la conclusión conmovedora de la cautivadora saga del pequeño robot Wall-E, una aventura que comenzó con los fundamentos del aprendizaje automático y el aprendizaje supervisado. Desde sus primeros pasos en el reino de la inteligencia artificial, Wall-E evolucionó a través de diversos capítulos, explorando los principios básicos del aprendizaje automático, sumergiéndose en el estudio detallado de la regresión y, finalmente, escalando las cumbres complejas de la clasificación.
La primera etapa vio a Wall-E aprender los entresijos del aprendizaje supervisado, una disciplina que le permitió comprender cómo utilizar una base de datos para entrenar un modelo. Esta fase inaugural sentó las bases de su búsqueda para entender el complejo mundo de los datos y los algoritmos.
El segundo acto de esta saga sumergió al robot en el universo de la regresión, donde aprendió a predecir valores continuos en función de variables de entrada (el oro en función de su pureza). Este capítulo amplió sus horizontes, llevándolo a dominar conceptos como el descenso de gradiente y la función de costo, herramientas esenciales en su caja de herramientas de aprendizaje automático.
Finalmente, el último episodio vio a nuestro aspirante a científico de datos enfrentarse a la clasificación, un desafío aún más complejo que implicaba la distinción entre diferentes tipos de componentes electrónicos. Desde sus humildes comienzos con la clasificación binaria (metal-plástico), evolucionó hacia una audaz exploración de la clasificación multiclase (selección de metales preciosos), destacando técnicas como el algoritmo de los k vecinos más cercanos y la selección cuidadosa de modelos.
Así, esta conmovedora conclusión de la saga de Wall-E simboliza no solo el fin de una historia excepcional, sino también la realización de un aprendizaje progresivo y metódico en el vasto reino del aprendizaje automático. El pequeño robot clasificador de desechos ha recorrido un camino impresionante, desde la comprensión de los conceptos básicos hasta la maestría de técnicas sofisticadas, dejando atrás un legado de aprendizaje y perseverancia. Esta saga, rica en lecciones, se cierra con la certeza de que Wall-E está ahora listo para enfrentar nuevos desafíos en el complejo mundo de la inteligencia artificial. Quién sabe, tal vez algún día logre igualar a EVE, abriendo así el camino a nuevas exploraciones y descubrimientos.

Bibliografía
G. James, D. Witten, T. Hastie et R. Tibshirani, An Introduction to Statistical Learning, Springer Verlag, coll. « Springer Texts in Statistics », 2013.
D. MacKay, Information Theory, Inference, and Learning Algorithms, Cambridge University Press, 2003.
T. Mitchell, Machine Learning, 1997.
F. Galton, Kinship and Correlation, Statistical Science, Institute of Mathematical Statistics, vol. 4, no 2, 1989, p. 80–86, 1989.
C. Bishop, Pattern Recognition And Machine Learning, Springer, 2006.
G. Saint-Cirgue, Machine Learnia, Youtube Channel.
J. Tolles, W-J. Meurer, Logistic Regression Relating Patient Characteristics to Outcomes. JAMA. 316 (5): 533–4, 2016.
B-V. Dasarathy, Nearest Neighbor (NN) Norms: NN Pattern Classification Techniques, 1991.
G. Shakhnarovich, T. Darrell, P. Indyk, Nearest-Neighbor Methods in Learning and Vision, 2005.
Hastie, Tibshirani, Friedman, The elements of statistical learning. Springer. p. 195, 2009.
S. Konishi, G. Kitagawa, Information Criteria and Statistical Modeling, Springer, 2008.
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import os
print("Current Working Directory:", os.getcwd())
from sklearn.pipeline import make_pipeline
from sklearn.preprocessing import StandardScaler
from sklearn.linear_model import LogisticRegression
from sklearn.model_selection import train_test_split, GridSearchCV
from sklearn.preprocessing import OrdinalEncoder
# Replace 'path/to/your/excel/file.xlsx' with the actual path to your Excel file
excel_file_path = 'PlasticMetal_data.xlsx'
# Read the Excel file
result_df = pd.read_excel(excel_file_path)
# Display the Pandas DataFrame
print(result_df)
X = result_df['Density']
y = result_df['Material']
# Data preparation
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)
# Convert labels to the appropriate format for binary classification
ordinal_encoder = OrdinalEncoder(categories=[['Plastic', 'Metal']])
y_train_encoded = ordinal_encoder.fit_transform(y_train.values.reshape(-1, 1))
y_test_encoded = ordinal_encoder.transform(y_test.values.reshape(-1, 1))
# Reshape y_train and y_test
y_train_reshaped = y_train_encoded.ravel()
y_test_reshaped = y_test_encoded.ravel()
# Reshape X_train and X_test
X_train_reshaped = X_train.values.reshape(-1, 1)
X_test_reshaped = X_test.values.reshape(-1, 1)
# Create the model
model = make_pipeline(StandardScaler(), LogisticRegression(random_state=42))
print(model)
# Create parameter dictionary
params = {
'logisticregression__penalty': ['l2', None],
'logisticregression__solver': ['lbfgs'],
'logisticregression__max_iter': [100, 200, 300, 500, 1000]
}
# Create a search grid
grid = GridSearchCV(model, param_grid=params, cv=5)
# Train the model
grid.fit(X_train_reshaped, y_train_reshaped)
print(grid.best_params_)
print(grid.best_score_)
modelB = grid.best_estimator_
# Model evaluation
accuracy = modelB.score(X_test_reshaped, y_test_reshaped)
print(f"Model accuracy: {accuracy}")
# Predictions
predictions = modelB.predict(X_test_reshaped)
print(predictions)
print(ordinal_encoder.inverse_transform(np.array([[1], [0]])))
coefficients = modelB.named_steps['logisticregression'].coef_
intercept = modelB.named_steps['logisticregression'].intercept_
print("Coefficients:", coefficients)
print("Intercept:", intercept)
# Plot the sigmoid function with normalized data
density_values = np.linspace(0, X_train_reshaped.max(), 300).reshape(-1, 1)
probabilities = modelB.predict_proba(density_values)[:, 1]
# Find the density corresponding to a probability of 0.5
decision_boundary = density_values[np.argmax(probabilities >= 0.5)]
# Plot the sigmoid function
plt.figure(figsize=(10, 6))
plt.scatter(X_train_reshaped, y_train_reshaped, c=y_train_reshaped, cmap='Dark2_r', alpha=0.5)
plt.plot(density_values, probabilities, color='blue', linewidth=2, label='Sigmoid Function')
# Add the vertical line corresponding to a probability of 0.5
plt.axvline(x=decision_boundary, color='red', linestyle='--', label='Decision Boundary')
plt.title('Final Representation of the Sigmoid Function')
plt.xlabel('Density')
plt.ylabel('Probability of Metal')
plt.grid(ls='--')
plt.legend()
plt.show()
# Suppose you have a new material with a certain density
new_material_density = 4 # Replace this value with the actual density of your new material
new_material_density_reshaped = np.array(new_material_density).reshape(-1, 1)
print(modelB.predict(new_material_density_reshaped))
# Make the prediction with the model
probability_of_metal = modelB.predict_proba(new_material_density_reshaped)[:, 1]
# Display the result
print("Probability of being metal:", probability_of_metal)
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import os
print("Current Working Directory:", os.getcwd())
from sklearn.pipeline import make_pipeline
from sklearn.preprocessing import MinMaxScaler
from sklearn.neighbors import KNeighborsClassifier
from sklearn.model_selection import train_test_split, GridSearchCV, validation_curve, learning_curve
from sklearn.preprocessing import LabelEncoder
# Replace 'path/to/your/excel/file.xlsx' with the actual path to your Excel file
excel_file_path = 'metals_samples.xlsx'
# Read the Excel file
result_metals_df = pd.read_excel(excel_file_path)
# Display the Pandas DataFrame
print(result_metals_df)
X = result_metals_df[['Density', 'Electrical Conductivity']]
y = result_metals_df['Metal Type']
# Data preparation
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)
# Convert labels to the appropriate format for binary classification
label_encoder = LabelEncoder()
y_train_encoded = label_encoder.fit_transform(y_train)
y_test_encoded = label_encoder.transform(y_test)
# Create the model
model = make_pipeline(MinMaxScaler(), KNeighborsClassifier())
print(model)
# Create parameter dictionary
params = {
'kneighborsclassifier__n_neighbors': [2,3,4,5,6,7,8,9,10, 15, 20, 25, 30, 40, 100],
'kneighborsclassifier__weights': ['uniform', 'distance'],
'kneighborsclassifier__p': [1, 2]
}
# Create a search grid
grid = GridSearchCV(model, param_grid=params, cv=5)
# Train the model
grid.fit(X_train, y_train_encoded)
print(grid.best_params_)
print(grid.best_score_)
modelB = grid.best_estimator_
# Model evaluation
accuracy = modelB.score(X_test, y_test_encoded)
print(f"Model Accuracy: {accuracy}")
# Predictions
predictions = modelB.predict(X_test)
#for i in range(0, 32):
#print(label_encoder.inverse_transform(np.array([i])))
# Sample
X_sample = pd.DataFrame({'Density': [7.5], 'Electrical Conductivity': [5.8], 'Metal Type' : [np.NaN]})
X_sample = X_sample[['Density','Electrical Conductivity']]
# Predict using the scaled sample
prediction = modelB.predict(X_sample)
prediction_proba = modelB.predict_proba(X_sample)
print("Predicted Metal Type:", label_encoder.inverse_transform(prediction))
print("Prediction Probabilities:", prediction_proba)
# Probability Prediction
prediction_proba = modelB.predict_proba(X_sample)
# Validation Curves
k_range = np.arange(1,100)
#train_score, val_score = validation_curve(model, X_train, y_train_encoded, param_name='kneighborsclassifier__n_neighbors',param_range=k_range, cv =5)
#plt.plot(k_range,val_score.mean(axis=1), label='Validation')
#plt.plot(k_range,train_score.mean(axis=1), label='Train')
#plt.xlabel('Number of Neighbors (k)')
#plt.ylabel('Score')
#plt.grid(ls='--')
#plt.legend()
#plt.title('Validation and Train Curves for k-NN')
#plt.show()
# Learning curves
#N, learn_train_score, learn_val_score = learning_curve(modelB, X_train, y_train_encoded, train_sizes=np.linspace(0.01, 1.0, 50), cv = 5)
#print(N)
#plt.plot(N,learn_val_score.mean(axis=1), label='Validation')
#plt.axhline(y=0.957, c='red', ls='--', label = 'Threshold')
#plt.plot(N,learn_train_score.mean(axis=1), label='Train')
#plt.xlabel('Train Sizes')
#plt.ylabel('Score')
#plt.grid(ls='--')
#plt.legend()
#plt.title('Validation and Train Learning Curves for k-NN')
#plt.show()
# Displaying probabilities with class names
for i, metal_class in enumerate(label_encoder.classes_):
print(f"Probability for class '{metal_class}': {prediction_proba[0, i]}")
plt.figure(figsize=(10, 6))
scatter = plt.scatter(X_train['Density'], X_train['Electrical Conductivity'], c=y_train_encoded, cmap='Dark2_r', alpha=0.5)
plt.scatter(X_sample['Density'], X_sample['Electrical Conductivity'], c='red', s=50, marker='X', alpha=0.8)
plt.axvline(x=tuple(X_sample['Density']), c='red', ls='--', alpha=0.8)
plt.axhline(y=tuple(X_sample['Electrical Conductivity']), c='red', ls='--', alpha=0.8)
plt.xlabel('Density')
plt.ylabel('Electrical Conductivity (S/m)')
plt.grid(ls='--')
# Configure the colorbar correctly
cbar = plt.colorbar(scatter, ticks=range(len(label_encoder.classes_)))
cbar.set_label('Metal Alloys')
cbar.set_ticklabels(label_encoder.classes_)
plt.title('Unknown Metallic Sample Based on Density and Electrical Conductivity')
plt.legend()
plt.show()



