Wall-E: El Pequeño Minero de Oro
Episodio II
Por Jordan Moles el 2 de noviembre, 2023

A diferencia de sus homólogos robóticos del pasado, Wall-E se destacaba por su curiosidad insaciable y su deseo de aprender. Cada día, se aventuraba en los rincones olvidados del planeta, en busca de tesoros enterrados y pasados por alto. Durante una de sus expediciones, en una antigua mina abandonada, Wall-E hizo un descubrimiento notable: muestras de oro centelleantes, ocultas bajo capas de tierra y roca. Intrigado por estos destellos dorados, se preguntó si podría divertirse estimando su valor.
Como un erudito robótico, sabía que la evaluación del precio de estas pepitas dependía de su pureza. Fue en ese preciso momento que se dispuso a explorar un problema de extrema simplicidad: la Regresión Lineal.
Se recomienda encarecidamente haber leído el Episodio I antes de continuar !
En las Profundidades del Conocimiento: la Regresión
La historia de nuestro intrépido robot solitario continúa y se enfrenta a una categoría fascinante de problemas: la regresión. Estos enigmas lo impulsan a desarrollar nuevas habilidades para estimar valores numéricos en función de datos de entrada, y ocupan un lugar destacado en su amplio repertorio de exploraciones.
Wall-E, el pequeño robot recolector de basura, se encuentra con problemas de regresión cada vez que desea predecir un valor numérico basado en ciertas características o variables continuas. Imagínenlo analizando los datos que ha recopilado mientras se esfuerza por determinar el precio de una pepita de oro en función de su pureza. En esta búsqueda, debe establecer una relación matemática entre los datos que tiene, como la pureza del oro, y los valores que desea predecir, es decir, los precios de estas valiosas pepitas.
Una de las dificultades que enfrenta Wall-E es elegir el modelo de regresión adecuado. Se pregunta si debe optar por una regresión lineal simple, lo que significa que supone una relación lineal entre la pureza del oro y su precio, o si debe explorar modelos más complejos, como una regresión polinómica. La elección del modelo es crucial ya que afectará la precisión de sus predicciones.
Otro problema que Wall-E debe resolver es cómo evaluar el rendimiento de su modelo. No puede permitirse cometer errores en sus estimaciones, ya que un error en la estimación del precio del oro podría tener consecuencias potencialmente desastrosas. Por lo tanto, explora diversas medidas de error, como el error absoluto medio y la raíz cuadrada del error cuadrático medio (por ahora, es un galimatías), para evaluar la precisión de sus predicciones.
Uno de los desafíos más intrigantes a los que se enfrenta Wall-E en los problemas de regresión es la optimización de los parámetros del modelo. Debe recorrer un proceso iterativo de ajuste de estos parámetros para minimizar el error entre sus predicciones y los valores reales. Wall-E se embarca en la descenso del gradiente, una técnica que lo ayuda a encontrar los parámetros óptimos al minimizar una función de costo que recopila los errores del modelo.
Cada problema de regresión que Wall-E aborda es único, ya que los datos y los objetivos varían. Sin embargo, su perseverancia e ingenio, combinados con sus habilidades en Aprendizaje Automático, le permiten superar estos desafíos y estimar con precisión los valores numéricos, ya sea el precio del oro u cualquier otra tarea de regresión.
La Cosecha
Poco después de la fuga de la humanidad, el joven robot sintió como un viento de soledad invadía sus circuitos impresos. Para pasar el tiempo, después de un día de arduo trabajo, recorre terrenos lejanos, busca en los escombros de las grandes reservas de oro, analiza cada uno de los aleaciones preciosas, examina cada pequeña pepita de oro para determinar su pureza y enumera todos los ejemplos de oro terrestre mostrándolos en una tabla con sus respectivos precios (aquí están los primeros 5 ejemplos de los 150).
| Pureza del oro | Precio del oro | |
|---|---|---|
| Muestra 1 | 0.3745 | 1028.1347 |
| Muestra 2 | 0.9507 | 1456.2091 |
| Muestra 3 | 0.7320 | 1260.2042 |
| Muestra 4 | 0.5987 | 1145.5583 |
| Muestra | 0.1560 | 958.0828 |
Cuando se indican, esta tabla constituye una base de datos de entrenamiento. Cada muestra \(k\) está caracterizada por dos elementos: su pureza \(x^{(k)}\), que varía entre 0 (no es oro) y 1 (es oro puro), y su precio \(y^{(k)}\) (que puede ir de 0 a infinito).
La recopilación de estas muestras representa un momento crucial en la vida de este robot científico. Aquí hay dos aspectos esenciales que debe tener en cuenta para realizar estimaciones precisas.
Amplio rango de datos: Wall-E se da cuenta rápidamente de que para obtener estimaciones confiables, debe tener un gran número de muestras en su base de datos.
De hecho, si solo se consideran dos muestras, como se ilustra aquí, es imposible determinar si el comportamiento de los precios es lineal o no.
Muchas curvas de estimación podrían pasar por estos dos puntos sin reflejar la realidad. Como las dos curvas a continuación, por ejemplo.

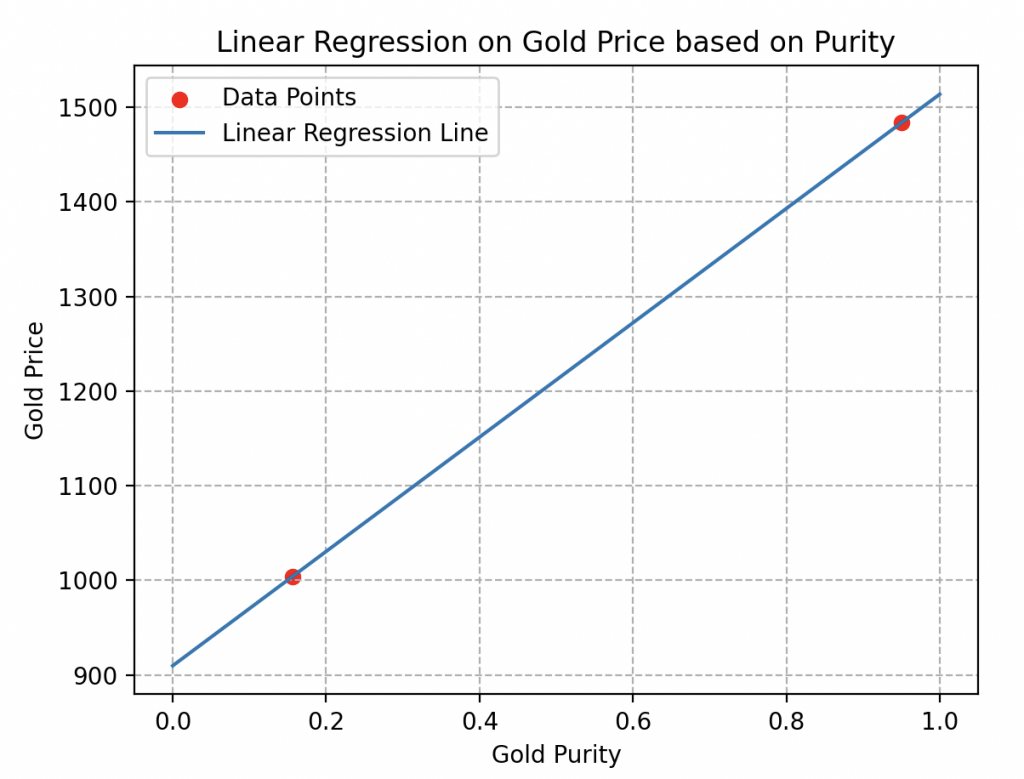


Diversidad de datos: otro detalle crucial a tener en cuenta durante la recolección es la variedad de datos.
Supongamos que Wall-E solo tiene en cuenta muestras puras o muestras con pureza extremadamente cercana (ver la figura adjunta).
En esta situación, todas las muestras tendrán casi el mismo precio, lo que le impediría estimar el precio de otras aleaciones de oro.

Conclusión de la recolección: es imperativo reunir una multitud de muestras seleccionadas al azar para evitar estas limitaciones y garantizar la obtención de estimaciones precisas para una amplia variedad de aleaciones de oro.
Creación del modelo lineal
A partir de estos datos, Wall-E elabora lo que hemos llamado un modelo lineal \(f(x)=ax+b\), donde \(a\) y \(b\) son los parámetros del modelo.
Un modelo eficiente minimiza las discrepancias entre las predicciones de Wall-E \(f(x)\) y los valores reales \(y\) de las muestras. Como una especie de buscador de oro moderno, Wall-E ajusta estos parámetros para alinear mejor sus estimaciones con la realidad, creando así una ecuación que vincula sutilmente la pureza y el valor del oro. Aquí está su intento inicial, que no es asombroso en absoluto.


Medir los Tesoros de Oro: La Función de Costo
La siguiente etapa en el aprendizaje de Wall-E implica evaluar el rendimiento de este modelo, es decir, medir los errores entre sus predicciones y los valores en el conjunto de datos.
Para el pequeño robot, el procedimiento es simple: cada estimación, denotada como k, en el conjunto de datos se enfrenta a la realidad. Según el enfoque elegido, el programa de Wall-E devuelve el error correspondiente a cada predicción que llamaremos \(err(k)\).
Cada una de las estimaciones de Wall-E está así asociada con su propia margen de error. Con el tiempo, estos errores se acumulan hasta alcanzar el número total de ejemplos n en el conjunto de datos.
Entonces, se reúnen todos estos errores en una función que llamamos función de costo, denotada como \(Γ(a, b)\). Es una función que depende de los parámetros a ajustar y simplemente calcula el promedio de todos los errores. Se escribe de la siguiente manera:
\[
\Gamma(a, b) = \frac{err(1) + err(2) + \cdots + err(n)}{n} = \frac{1}{n}\sum_{k=1}^n err(k)
\]
Una propiedad importante a tener en cuenta sobre esta función es su convexidad, es decir, que su curva «mira hacia arriba en todas partes». Más específicamente, esto significa que si trazamos una línea entre dos puntos de la curva, esta siempre estará por encima o al nivel de la curva. ¡Tales curvas siempre tienen un mínimo global! Esto es lo que nos será útil más adelante.

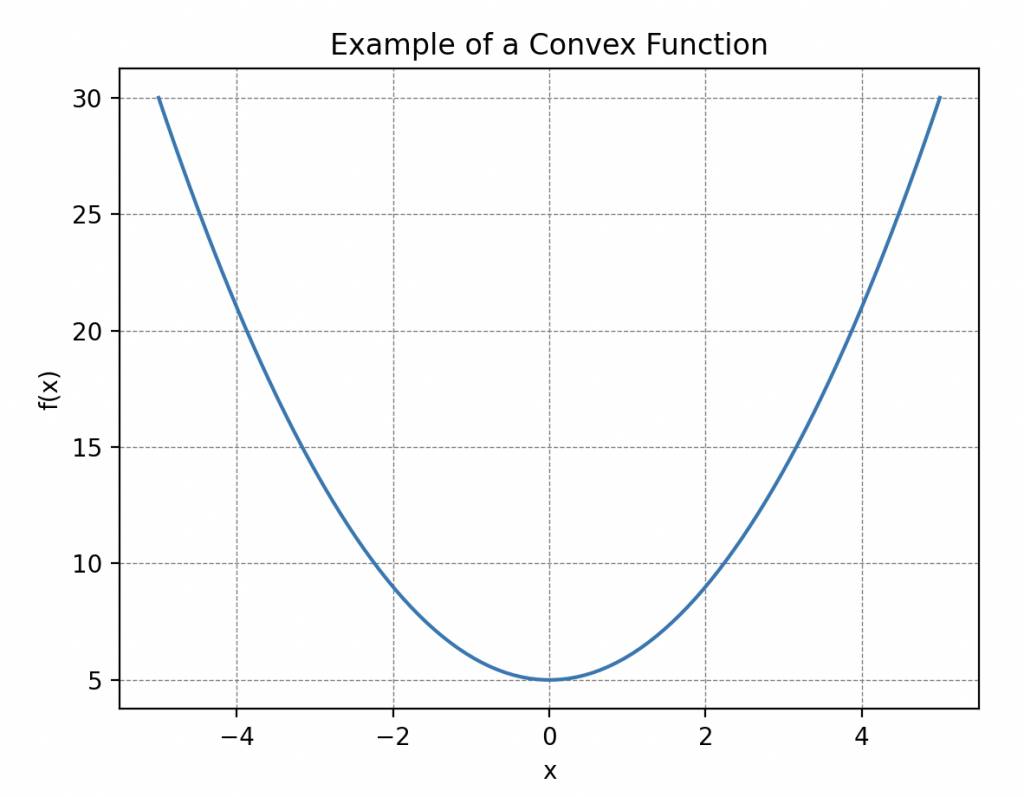
Sin embargo, ¿qué es el error? ¿Cómo se puede definir? Antes de abordar estas preguntas, es crucial hablar sobre un concepto matemático: la distancia, que permite cuantificar la separación entre dos puntos dados.
Las Distancias Explicadas por Hal
Wall-E, en pleno momento de reflexión, buscaba entender por qué debía prestar atención al concepto de distancia. La perplejidad lo invadía mientras observaba a Hal, su leal compañero cucaracha, deslizarse sigilosamente entre los rincones del laboratorio.
¿Qué significado podría tener esta exploración minuciosa y metódica del espacio por parte de Hal?

Estaba lejos de imaginar que detrás de esos movimientos silenciosos y discretos, Hal compartía, a su manera, las sutilezas de las distancias. Cada desplazamiento entre los objetos de la habitación ilustraba una regla matemática esencial. Eran un total de cuatro.
La Positividad. En esta coreografía, Hal demostraba la primera: la positividad de las distancias. Explicaba a su manera que la distancia entre su escondite favorito y la despensa de desechos siempre era positiva, un hecho simplemente ilustrado por su trayectoria (una longitud no es negativa).
Wall-E, como buen científico, lo expresó en términos matemáticos: la distancia entre dos puntos A y B cualesquiera debe ser positiva o nula. Esto se escribe,
\begin{align*}
\forall A, B \in E, \quad d(A,B)\geq 0.
\end{align*}
Este símbolo «\(\forall\)» significa «para todo» y «\(\in\)» significa «en». Esto se lee, para todos los elementos A y B (aquí se trata de puntos) en E, la distancia entre A y B es positiva o nula.
La Simetría. El concepto de simetría fue luego destacado por Hal, demostrando cómo sus desplazamientos de un punto A a un punto B eran siempre idénticos, ya fuera de B a A o de A a B. Sus idas y venidas sutiles marcaban así la idea de simetría en esta danza entre los puntos.
El pequeño robot introdujo esta idea en sus circuitos: la distancia entre A y B debe ser la misma que entre B y A. Matemáticamente,
\begin{align*}
\forall A, B \in E, \quad d(A,B)=d(B,A).
\end{align*}
La Separación. Sin embargo, la demostración más sorprendente para Wall-E fue la de la separación. Hal fue a buscar dos semillas que colocó en dos lugares diferentes de la habitación. Luego, comenzó una danza frenética dejando una semilla quieta y llevando la otra hacia ella en una serie de idas y venidas rápidas, para finalmente unir las dos semillas.
De esta manera, Hal quiso ilustrar a Wall-E que si la distancia entre estos dos puntos era nula, entonces los dos puntos coincidían. Una representación impresionante y clara de la regla de separación.
Wall-E entendió la lección, que tradujo a su propio lenguaje: si la distancia entre A y B es cero, entonces A y B coinciden.
\begin{align*}\forall A, B \in E, \quad d(A,B)=0 ⇒ A=B.\end{align*}
El símbolo «⇒» significa «implica».
La Desigualdad Triangular. Sin embargo, la lección de Hal no se detuvo ahí, ya que aún quedaba una regla esencial por analizar. Hal continuó su exploración ilustrando la desigualdad triangular.
Al moverse entre su escondite, Wall-E y la despensa, Hal mostró que la distancia entre su escondite y Wall-E siempre es menor que la distancia entre su escondite y la despensa más la distancia entre la despensa y Wall-E. Esta astuta demostración, que enseñaba que el camino más corto entre dos puntos era una línea recta, cautivó a Wall-E.
Se apresuró a transcribir todo esto: Si tomo tres puntos A, B y C que no coinciden, entonces la distancia entre A y B siempre es menor o igual a la distancia entre A y C más la distancia entre C y B.
\begin{align*}
\forall A, B, C \in E, \quad d(A,B)\leq d(A,C)+d(C,B).
\end{align*}
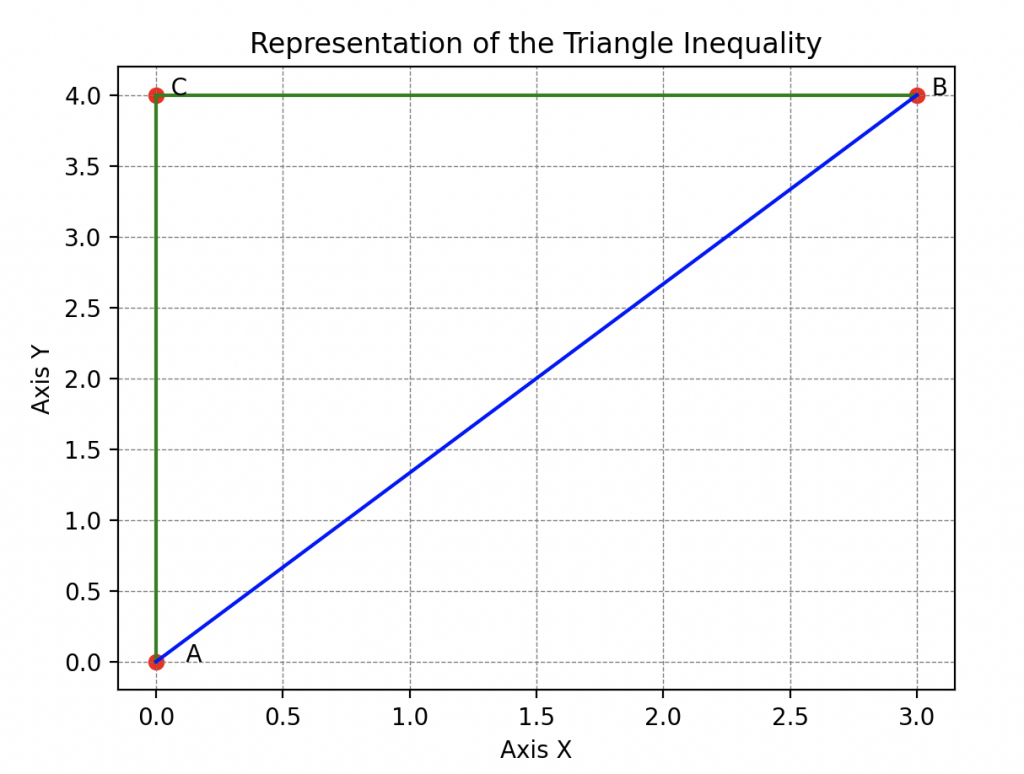

Gracias a Hal, Wall-E asimila formalmente que una distancia es una función que compara dos puntos en un espacio dado, asignándoles un número real no negativo que expresa la «longitud» entre estos dos puntos, y que sigue reglas bien definidas.
Este espacio puede ser el plano familiar de dos dimensiones, como lo mostró la cucaracha, o nuestro espacio tridimensional, e incluso espacios mucho más exóticos.
Sus habilidades de abstracción también le permiten comprender que existen diferentes tipos de distancias, entre las cuales la más conocida es la distancia euclidiana (también conocida como la 2-distancia).
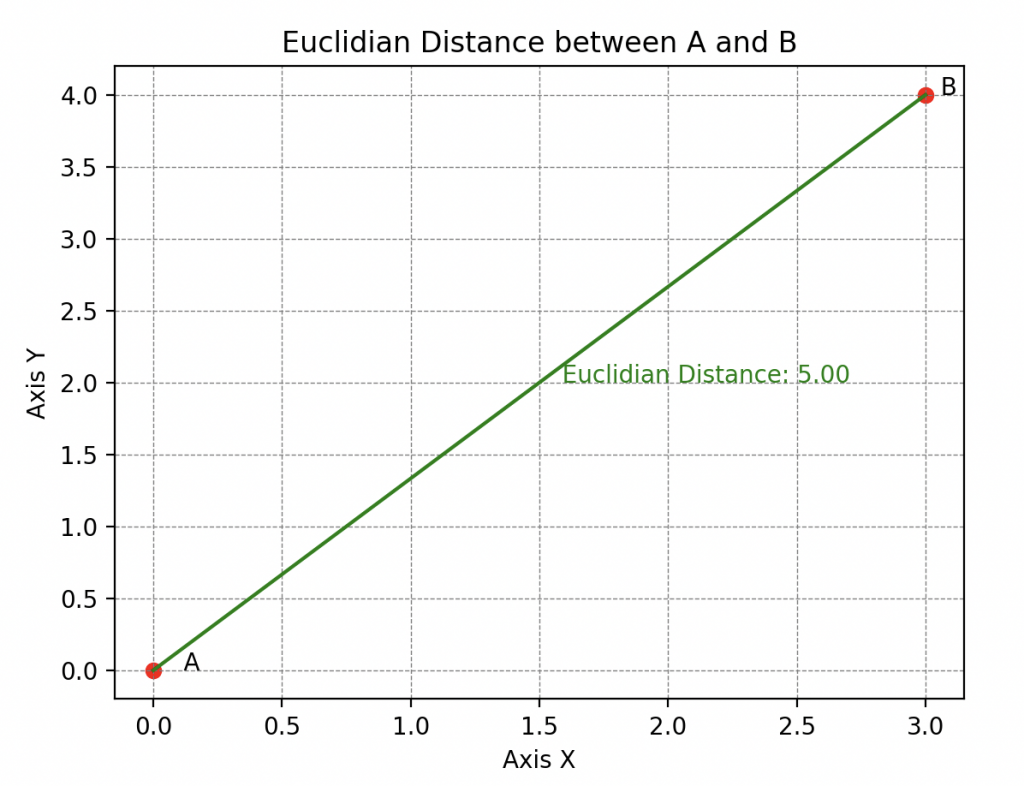

o incluso la distancia \(\infty\) (se dice distancia infinito) que evalúa la distancia máxima entre estos puntos a lo largo de cualquier dimensión.
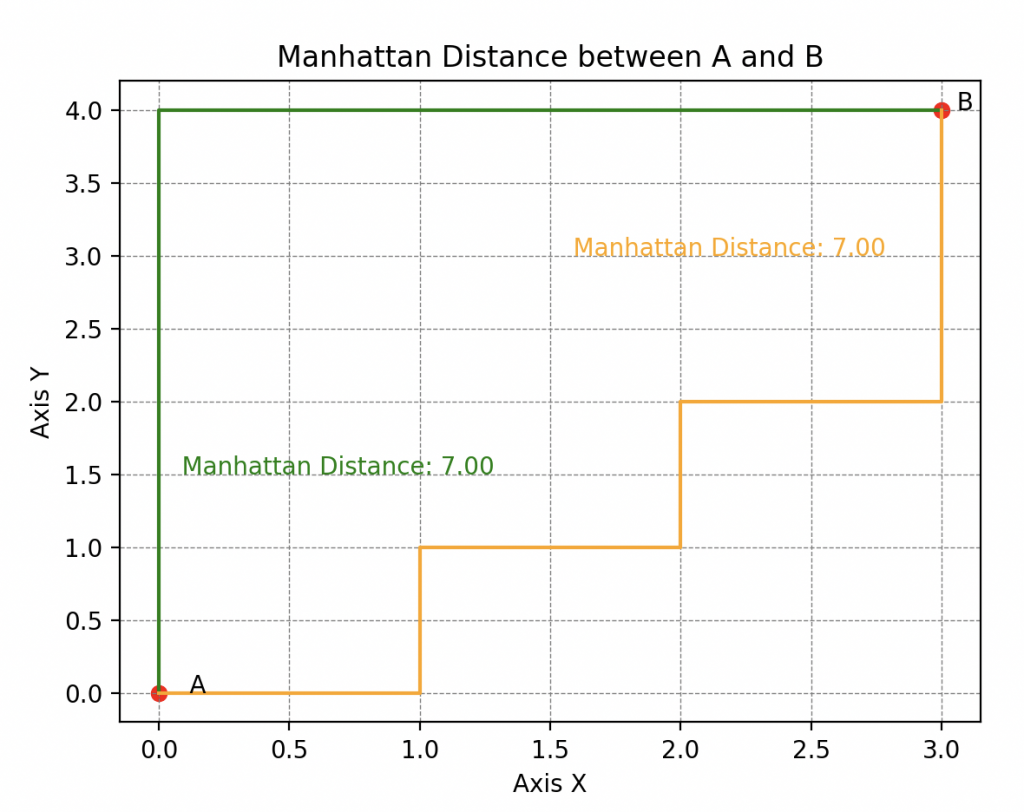
Pero también encontramos la distancia de Manhattan (o 1-distancia para los puristas) que se llama así porque refleja la distancia que debería recorrer un taxi en una red de calles que forman cuadrículas ortogonales (típico de la disposición de las calles en Manhattan, de ahí su nombre).
Exploraremos en detalle estas particularidades en un próximo artículo.
Un Error Fatal
Ahora, ¿por qué abordar el concepto de distancia en el contexto de la evaluación de las predicciones de Wall-E? De hecho, esto nos lleva a reflexionar sobre cuáles son realmente los errores entre las predicciones y los valores reales del conjunto de datos.
Imagina que Wall-E evalúa la primera muestra, una aleación de oro de un kilo con una pureza de 0.72 y un precio real de 1231 pernos, pero predice 1331 pernos. Observas una diferencia de -130 pernos. Aquí obtenemos un valor negativo, pero en otro ejemplo podría ser positivo. Esta dualidad entre valores positivos y negativos no es práctica.
Para resolver este problema, tenemos dos opciones:
• La primera opción es considerar el valor absoluto de cada diferencia (eliminamos el signo negativo cuando está presente). El error resultante se llama error absoluto, notado AE (Absolute Error en inglés).
En el ejemplo anterior, tendríamos \(AE(1) = | 1231-1331| = |-130|=130\).
• La segunda opción es calcular el cuadrado de cada diferencia. Este error se llama error cuadrático, notado SE (Squared Error en inglés).
En este caso, tendríamos un error cuadrático \(SE(1)= (1231-1331)^2=(-130)^2=16900\).
Se observa que la segunda opción amplifica enormemente los errores, pero veremos cómo equilibrar estas diferencias más adelante.
Así que, al aplicar una u otra de estas opciones, elegimos la forma en que queremos medir los errores, es decir, una distancia. La \(\infty\)-distancia para la primera o la distancia euclidiana para la segunda.
Ahora, el procedimiento es sencillo: cada estimación, denotada como k, en el Dataset se compara con la realidad. Según el enfoque elegido, el programa de Wall-E devuelve el error correspondiente. Además, según la distancia elegida, la función de costo tiene un nombre diferente:
Para volver a la escala original nuestros errores calculados por esta función, simplemente tomaremos su raíz cuadrada. La función resultante se llama la raíz cuadrada del error cuadrático medio, notada RMSE (Root Mean Squared Error en inglés).
Aquí tienes un ejemplo para ilustrar el cálculo donde Wall-E estima el valor de solo cinco ejemplos (con cinco diferencias).
| Diferencias | -100 | 7 | -2 | 42 | 13 |
| Errores AE | 100 | 7 | 2 | 42 | 13 |
| Errores SE | 10 000 | 49 | 4 | 1764 | 169 |
Cálculo de la MAE
Cálculo de la RMSE
\begin{align*}MAE(a, b) =\frac{100 + 7 + 2 + 42 + 13}{5} = 32.8.\end{align*}
\begin{align*}RMSE(a, b) =\sqrt{\frac{10000 + 49 + 4 + 1764 + 169}{5} }= 48.96.\end{align*}
¿Por qué elegir una u otra? Para responder a esta pregunta, presentemos a Eve.

Además de su capacidad para distinguir objetos orgánicos, ella tiene un sistema de autodefensa sofisticado. Se le ha entrenado para estimar la distancia (en centímetros) entre el impacto de sus disparos y el centro del objetivo. Eve entrena dos modelos para encontrar aquel que minimizará los errores.
| Error 1 | Error 2 | Error 3 | Error 4 | MAE | |
|---|---|---|---|---|---|
| Modelo 1 | 20 | 0 | 0 | 0 | 5 |
| Modelo 2 | 6 | 5 | 6 | 4 | 5.25 |
| Error 1 | Error 2 | Error 3 | Error 4 | RMSE | |
|---|---|---|---|---|---|
| Modelo 1 | 20 | 0 | 0 | 0 | 10 |
| Modelo 2 | 6 | 5 | 6 | 4 | 5.31 |
Aquí observamos que la MAE del modelo 1 es más pequeña que la del modelo 2, por lo que Eve elegirá el modelo 1 para estimar sus disparos.
Sin embargo, en el primer modelo observamos que Eve comete prácticamente ningún error, excepto en su primer disparo donde se equivoca por 20 cm. Una cantidad no despreciable y peligrosa, ya que podría herir a alguien si su arsenal no es lo suficientemente preciso.
En esta tabla, es completamente diferente; observamos que la RMSE del modelo 1 es mucho peor que la del modelo 2, ya que muestra un error mucho más grande.
Eve tenderá a elegir el modelo 2 en este caso. De hecho, la RMSE penaliza mucho más los errores grandes que la MAE.
Si Eve favorece la Mean Absolute Error (MAE), significa que quiere minimizar las diferencias absolutas entre el impacto de su disparo y el objetivo. Esto sugiere que, para Eve, cada diferencia tiene la misma importancia. Una diferencia de 20 unidades se considera veinte veces más importante que una diferencia de 1 unidad.
Por otro lado, si Eve elige favorecer la Root Mean Squared Error (RMSE), significa que quiere centrarse en las grandes diferencias. En este caso, los errores más importantes tienen un peso más significativo. De hecho, una diferencia de 20 unidades es 400 veces más importante que una diferencia de una unidad. Entonces, si Eve quiere eliminar los disparos con diferencias muy grandes, el modelo basado en RMSE sería más adecuado.
Estas elecciones de funciones de costo dependen de los objetivos de Eve: si quiere reducir las grandes diferencias, favorecerá el MSE. Por otro lado, si busca una evaluación equilibrada de todas las diferencias, optará por el MAE. También existen otras formas de medir los errores, pero no las discutiremos aquí.
Un Pequeño Paso para el Robot, un Gran Paso para el Algoritmo
Lo que más le gusta a Wall-E es aprender por sí mismo cuáles son los parámetros que minimizan la función de costo, es decir, los parámetros que nos ofrecen el mejor modelo posible. Para encontrar estos parámetros óptimos, Wall-E utiliza un conocido algoritmo de optimización llamado descenso de gradiente. Imaginen esta etapa como si Wall-E ajustara meticulosamente los botones de su modelo matemático para alcanzar el nivel de experiencia necesario en la tarea de predecir el precio del oro en función de su pureza
¡Descendemos!
La idea de la descente de gradiente es simple: imagina a Wall-E perdido en las laderas de una montaña de desechos en una densa niebla, reciclando lo que le queda por hacer. Desafortunadamente, sus baterías están empezando a agotarse peligrosamente y debe llegar a su pequeña nave que se encuentra en el punto más bajo, pero solo puede ver las pendientes inmediatas a su alrededor. Así que, con cada paso de longitud \(\delta\) (es la letra delta en griego), elige la dirección que le hace descender lo más rápido posible. A medida que avanza, ajusta su dirección según las pendientes que percibe, acercándose gradualmente al punto más bajo.
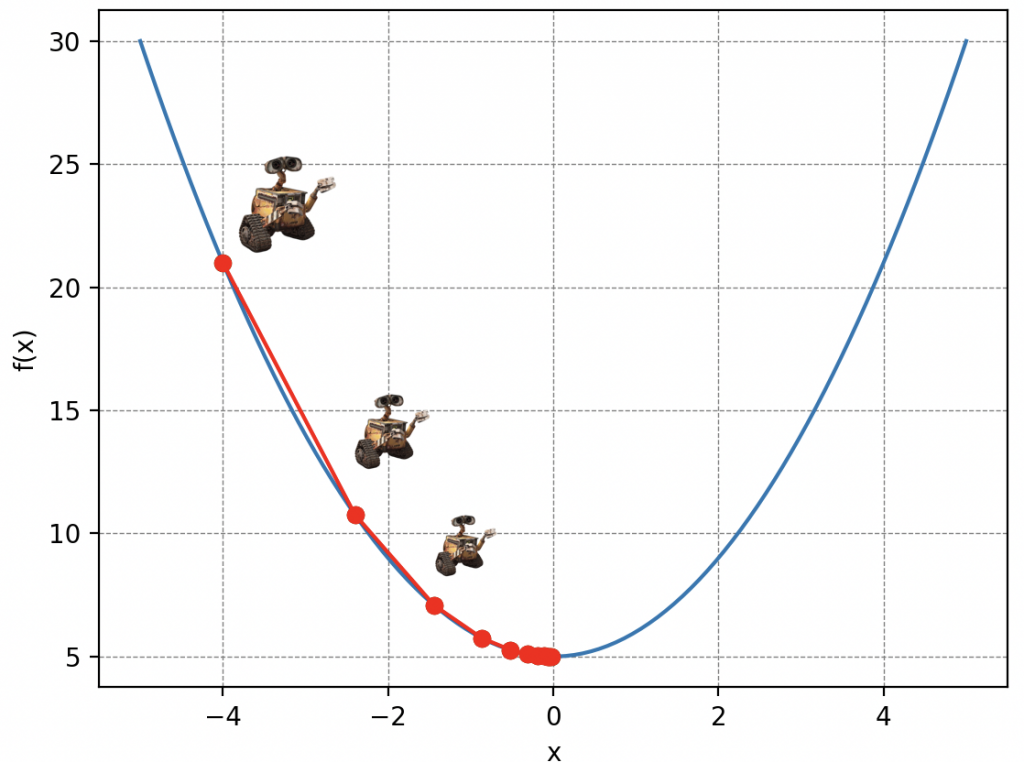

Por supuesto, la elección del valor \(\delta\) es crucial en la descente de gradiente. Si Wall-E da pasos demasiado pequeños, tardará demasiado en llegar abajo, o si usa su jetpack para volar distancias muy grandes, podría pasar por encima de su refugio.

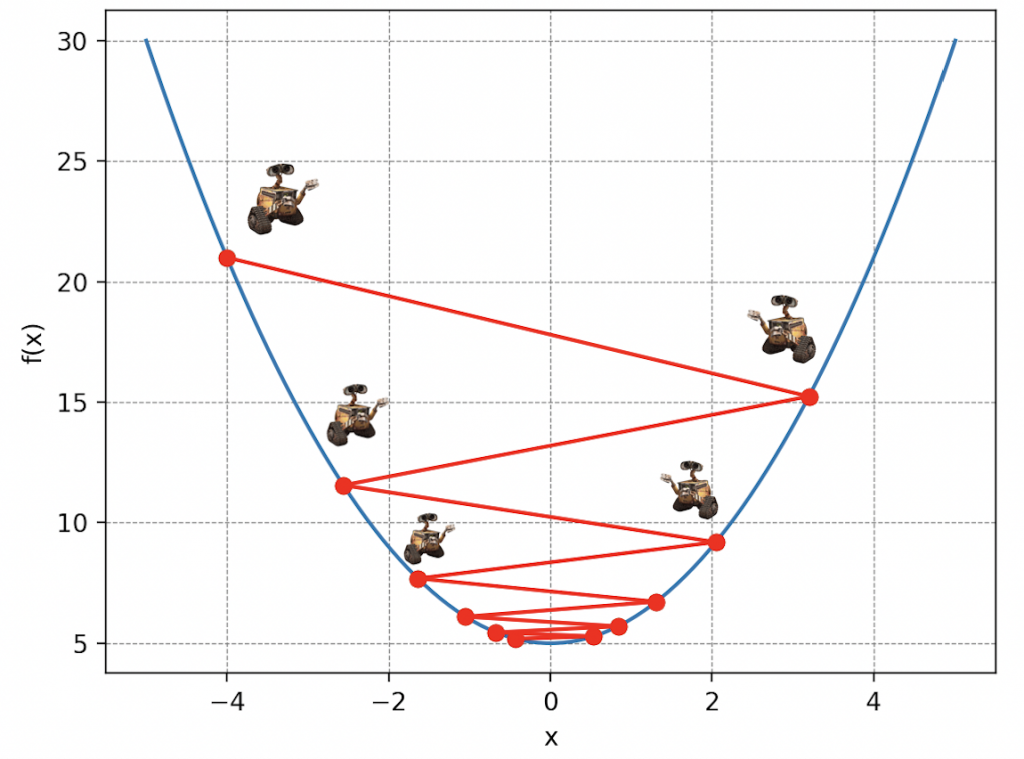
Volviendo a nuestro problema inicial. La montaña de desechos simboliza nuestra función de costo, los parámetros de la posición de Wall-E en la montaña representan los parámetros de nuestro modelo de regresión lineal y los pasos traducen lo que se llama la tasa de aprendizaje de Wall-E (Learning Rate en inglés). Así que, descomponiendo las acciones de Wall-E, algorítmicamente tenemos:
• Nuestro robot calcula los gradientes, es decir, la inclinación de la pendiente a lo largo de los dos ejes (a y b) de la función de costo en cada iteración. Matemáticamente, esto significa calcular estas dos cantidades:
\[
\frac{\partial \Gamma(a, b)}{\partial a} \quad\text{y}\quad \frac{\partial \Gamma(a, b)}{\partial b}
\]
Los matemáticos lo habrán entendido bien, esto no es más que el cálculo de la derivada de una función de varias variables.
• Actualiza los parámetros, acercándose cada vez más al mínimo de la función de costo. Llamamos a los nuevos parámetros \(a^*\) y \(b^*\) y se escriben de la siguiente manera:
\[
\begin{align*}
a^* &= a – \delta \times \frac{\partial \Gamma(a, b)}{\partial a} \\
b^* &= b – \delta \times \frac{\partial \Gamma(a, b)}{\partial b}
\end{align*}
\]
Así, los nuevos parámetros simplemente se definen como la posición anterior a la que restamos la tasa de aprendizaje \(\delta\) multiplicada por el valor de la pendiente. Por analogía, es la posición de Wall-E después de dar un paso en la dirección donde la pendiente es más pronunciada.
• Repite este proceso hasta encontrar el mínimo de la función de costo.
Es importante entender que la descenso de gradiente es un proceso iterativo, lo que significa que se repite muchas veces hasta que Wall-E alcance un punto donde la función de costo sea mínima y sus predicciones sean lo más precisas posible.
En cuanto a la tasa de aprendizaje, denotada como \(\delta\), algunos detalles merecen ser aclarados. Como en la metáfora anterior, la elección del valor de \(\delta\) es esencial.
Un \(\delta\) demasiado pequeño podría ralentizar la convergencia, ya que los ajustes a los parámetros serían minúsculos en cada paso, mientras que un \(\delta\) demasiado grande podría causar oscilaciones o incluso evitar la convergencia, ya que los ajustes podrían superar el mínimo deseado. Elegir sabiamente el valor de \(\delta\) es esencial para que el algoritmo de Wall-E converja de manera efectiva hacia la solución óptima.
¿Cuándo llegamos?
Hace un tiempo ya que nuestro valiente robot avanza desesperadamente a tientas, cegado por la madre naturaleza. Se pregunta cuándo llegará al pie de la montaña. Al igual que en esta situación, en aprendizaje automático, llegar al mínimo de la función de costo, el equivalente del refugio para Wall-E, puede parecer complicado. Su posición es incierta y para llegar allí, Wall-E debe ajustar su progreso teniendo en cuenta la longitud de sus pasos y la cantidad de estos.
Para orientarse, Wall-E debe registrar escrupulosamente cada una de sus posiciones a lo largo del flanco de la montaña, lo que llamamos la historia de la descenso. Al llevar un registro preciso de cada paso, puede luego trazar su trayectoria, creando así una ‘curva de descenso’. Esto le permite visualizar su camino recorrido, medir sus progresos y determinar si está cerca del punto más bajo. Aquí tienes un ejemplo, suponiendo que Wall-E esté colocado al azar en la montaña.


En el campo del aprendizaje automático, la historia de la bajada se llama, de hecho, la historia del costo, ya que proporciona los valores de la función de costo en función de variables clave como la tasa de aprendizaje y el número de iteraciones del algoritmo de descenso de gradiente.
De hecho, su representación gráfica, que llamamos curva de descenso, se llama en realidad curva de aprendizaje y es esencial para evaluar el rendimiento de un modelo, ya que ilustra de manera dinámica la evolución de la precisión del modelo.
En este caso particular, después de unas diez etapas, Wall-E parece dejar de descender más, indicando que ha llegado a su refugio. Los 40 pasos adicionales son, por lo tanto, inútiles. Esta información es crucial en informática, ya que nos permite evitar ejecutar innecesariamente el algoritmo, lo que puede ahorrar tiempo y recursos, especialmente cuando algunas simulaciones pueden llevar mucho tiempo, desde días hasta semanas.
Dentro de sus Circuitos Impresos: la Estimación del Precio del Oro
Pero, ¿qué sucede exactamente en el cerebro electrónico de nuestro adorable robot? Antes de realizar la más mínima adición, Wall-E traduce no solo el conjunto de datos en forma de tabla, sino también los parámetros del modelo y los gradientes: una especie de lenguaje cifrado para las máquinas conocido como forma matricial que simplifica enormemente los cálculos. Más precisamente, esto da lugar a un vector \(\mathbf{Y}\) compuesto por \(n\) elementos correspondientes al precio de los \(n\) ejemplares de oro.
acompañado de una matriz \(\mathbf{X}\) con \(n\) filas y \(m+1\) columnas que abarca con precisión cada característica \(m\) (aquí solo hay una característica, \(m=1\)) y una columna que contiene solo unos, llamada «sesgo».
Esta última nos permite realizar los cálculos matriciales necesarios para el aprendizaje. Es importante tener en cuenta que, en general, tenemos:
En paralelo, entra en escena un vector «parámetro» \(\mathbf{P}\) (una columna), que agrupa cuidadosamente todos los parámetros de nuestro modelo, es decir, \(a\) y \(b\).
No olvides que estamos buscando \(\mathbf{P}\) de manera que minimice la función de costo. Con esto, Wall-E puede expresar todas las etapas de aprendizaje fácilmente y estimar el precio de una pepita de oro con precio desconocido:
• La cosecha se realiza mostrando los datos en una matriz: cada muestra, con sus características de pureza y precio, encuentra su lugar en esta matriz.
• La Creación del Modelo es el proceso en el cual Wall-E define los parámetros mostrados en la columna \(\mathbf{P}\) tomados al azar, que sirven para establecer la relación lineal entre la pureza y el precio del oro \(\mathbf{F(\mathbf{X})}=\mathbf{X\times P}\).
• La Función de Costo se redefine de la siguiente manera: \begin{align*} \Gamma(\mathbf{P})=\frac{1}{n}\left(\mathbf{F(X)-y}\right)\cdot\left(\mathbf{F(X)-y}\right) \end{align*} donde \(\cdot\) es el producto escalar.
• Encontrar el mínimo implica calcular el gradiente:
\begin{align*}\frac{\partial }{\partial \mathbf{P}} \Gamma(\mathbf{P})=\frac{1}{n}\mathbf{X\cdot\left(F(X)-y\right)}\end{align*}
y aplicar iterativamente la descenso de gradiente para actualizar el parámetro P:
\begin{align*}\mathbf{P^*}=\mathbf{P}-\delta \frac{\partial }{\partial \mathbf{P}}\Gamma(\mathbf{P})\end{align*}
donde \(\mathbf{P^*}\) es el nuevo parámetro.
Wall-E, aplicando cuidadosamente todos los pasos, ¡está ahora listo para estimar el precio del oro según la pureza que le proporciones! Aquí está la curva final que obtiene.
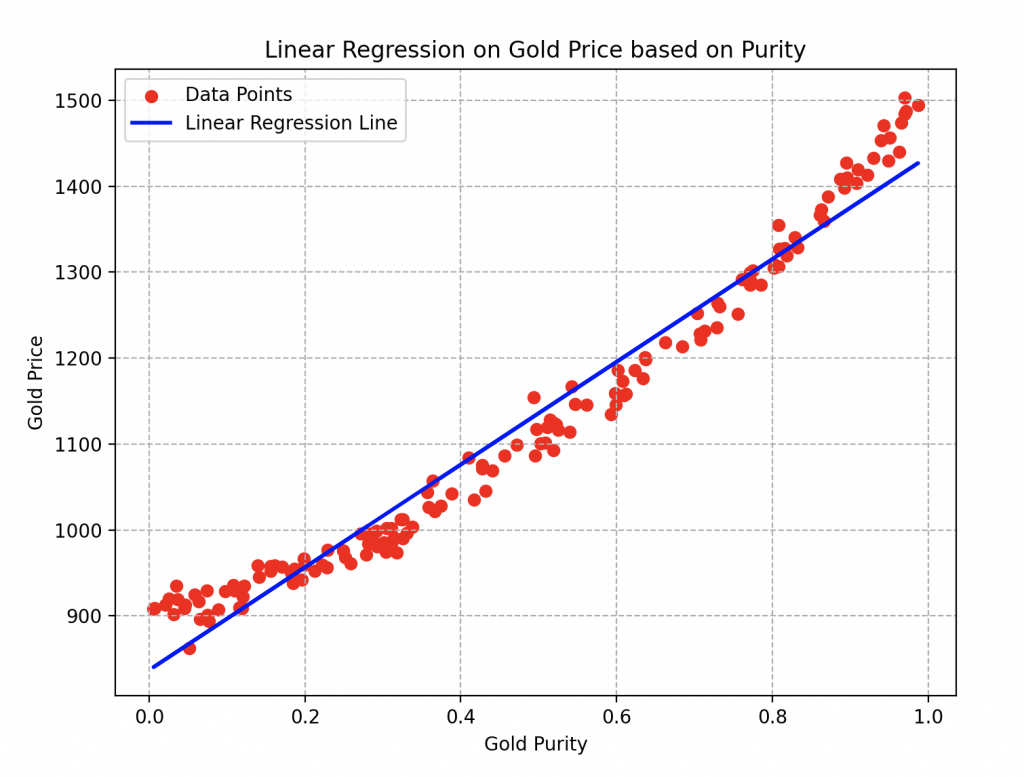
Los parámetros a y b de la recta en azul son respectivamente 493.56 y 886.18. Para la descenso de gradiente, de hecho, utilizó una tasa de aprendizaje igual a 0.2 y realizó alrededor de veinte iteraciones del algoritmo.
Así que podemos observar fácilmente que al elegir una aleación de oro con una pureza de 0.6, su precio se estimaría en alrededor de 1200 tornillos.
Transferencia de Conocimientos y Rendimiento del Modelo: Lecciones Aplicables a Todas las Regresiones
Todos los pasos y cálculos realizados para estimar el precio del oro en función de su pureza a través de una regresión lineal son fundamentalmente similares a los realizados para la regresión no lineal u otros tipos de modelos de aprendizaje automático.
Wall-E, el pequeño robot apasionado por la estimación del precio del oro, realiza una secuencia bien definida para entrenar su modelo, minimizar el error y ajustar los parámetros para predecir el precio del oro en función de su pureza. El proceso implica la transformación de los datos en matrices, la creación del modelo, la definición de la función de costo para evaluar los errores, la minimización de esta función ajustando iterativamente los parámetros y, finalmente, la obtención del parámetro óptimo para estimar con precisión el precio del oro.
Este proceso es flexible y se puede aplicar a diferentes situaciones y tipos de modelos de aprendizaje, adaptándose a problemas más complejos que requieren modelos más sofisticados. El éxito de Wall-E en la estimación del precio del oro muestra la potencia y eficacia de estos métodos, abriendo la puerta a aplicaciones más amplias y diversas del aprendizaje automático en contextos variados.
Pero aún queda una última cosa por ver: el coeficiente de determinación, también conocido como \(R^2\). Juega un papel crucial en la evaluación del rendimiento del modelo de Wall-E porque mide qué tan bien el modelo se ajusta a los datos en comparación con las variaciones de estos. En términos matemáticos, se escribe de la siguiente manera:
\[R^2 = 1 – \frac{\sum_{k=1}^{n} \left(y^{(k)}- f(x^{(k)})\right)^2}{\sum_{k=1}^{n} (y^{(k)}- \bar{y})^2}\]
donde \(\bar{y}\) es simplemente el promedio de los valores de nuestras muestras (en nuestro caso, simplemente el precio promedio). Bajo su apariencia complicada, simplemente se trata de una fracción fácil de entender. Reescribiéndolo de manera más comprensible, obtenemos:
\[R^2 = 1 – \frac{\text{Errores}}{\text{Varianza}}.\]
Recuerde (ver el artículo «Battre le Maître du Jeu») que la varianza es una medida de la dispersión de los valores de la muestra.
Así que, para Wall-E, obtener un \(R^2\) cercano a 1 sería ideal, lo que implicaría que la fracción a la derecha es cercana a 0. Esto significa que los errores son ampliamente despreciables en comparación con la forma en que se dispersan los datos y que el modelo propuesto por Wall-E se ajusta bien a los valores de la muestra.
Por otro lado, si \(R^2\) está cerca de 0, indicaría que el modelo no explica bien la variabilidad de los datos, y las predicciones pueden ser menos confiables porque los errores tienen el mismo orden de magnitud que la varianza.
Con todas estas explicaciones, Wall-E se embarcó en el cálculo del coeficiente de determinación \(R^2\) para evaluar la calidad de su modelo anterior.
El resultado es bastante gratificante, con una puntuación honorable de 0.93. En otras palabras, el modelo se ajusta notablemente bien a los datos, cubriendo aproximadamente el 93% de la variabilidad observada.
Un rendimiento que confirma la eficacia de su enfoque en la estimación del precio del oro en función de su pureza.

Sin embargo, Wall-E, como perfeccionista incansable, no se conforma con los éxitos ya obtenidos. Busca constantemente formas de mejorar su modelo.
Así que decide trascender el modelo lineal inicial optando por un enfoque polinómico (de grado 2). Modifica la función de referencia a \(f(x))=ax^2+bx+c\) y repite meticulosamente todos los pasos del algoritmo, dejando nada al azar. Aquí están los resultados que obtuvo.
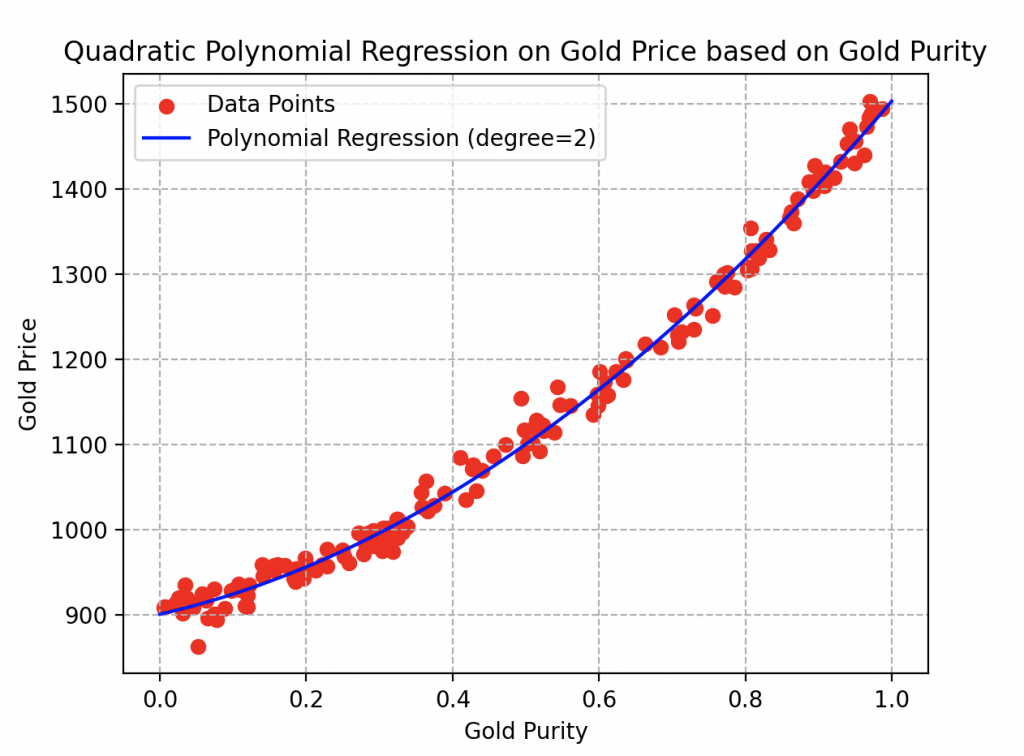
La curva se ajusta realmente bien a los datos y, como era de esperar, con parámetros que valen respectivamente 273.84, 404.43 y 837.08, ¡obtiene un notable coeficiente de determinación del 97 %!
Observa aquí que una muestra de oro con una pureza de 0.6 valdría aproximadamente 1160 pernos.
Al contemplar este éxito, no podemos dejar de anticipar con entusiasmo las futuras exploraciones de Wall-E en el complejo mundo de la modelización y el aprendizaje automático.
Exploración exitosa de los entresijos de la regresión: próximo paso, el fascinante mundo de la clasificación.
En esta fascinante exploración de los problemas de regresión, nos sumergimos en el apasionante universo de la modelización matemática, con Wall-E como intrépido guía. Desde las descensos de gradiente hasta las curvas de aprendizaje, pasando por la definición de errores, desmitificamos los aspectos clave de la regresión, revelando la magia subyacente del aprendizaje automático.
Mientras dejamos que Wall-E descanse sus circuitos después de sus hazañas en la regresión, prepárense para embarcarse en una nueva aventura en nuestro próximo artículo. Nos sumergiremos en los misterios de los problemas de clasificación, explorando cómo los modelos pueden aprender a categorizar y tomar decisiones en un mundo de datos complejos. ¡Manténganse conectados para sumergirse aún más en el dinámico universo del aprendizaje automático con Wall-E como su fiel compañero de viaje!
Bibliografía
G. James, D. Witten, T. Hastie et R. Tibshirani, An Introduction to Statistical Learning, Springer Verlag, coll. « Springer Texts in Statistics », 2013
D. MacKay, Information Theory, Inference, and Learning Algorithms, Cambridge University Press, 2003
T. Mitchell, Machine Learning, 1997
F. Galton, Kinship and Correlation (reprinted 1989), Statistical Science, Institute of Mathematical Statistics, vol. 4, no 2, 1989, p. 80–86
C. Bishop, Pattern Recognition And Machine Learning, Springer, 2006
G. Saint-Cirgue, Machine Learnia, Youtube Channel
D.V. Lindley, Regression and correlation analysis, 1987
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression
# Parameters of the quadratic function
a = 400
b = 200
c = 900
# Generate 150 points between -100 and 100
np.random.seed(42)
X = np.random.uniform(0, 1, 150)
# Create Y values based on the quadratic function with Gaussian noise
Y = a * X**2 + b * X + c + np.random.normal(0, 15, 150)
# Reshape the data for modeling
X = X.reshape(-1, 1)
Y = Y.reshape(-1, 1)
# Perform linear regression
model = LinearRegression()
model.fit(X, Y)
# Display the data
plt.figure(figsize=(8, 6))
plt.scatter(X, Y, color='red',label='Data Points')
plt.plot(X, 500 * X + c, color='blue', linewidth=2, label='Linear Regression Line')
#plt.plot(X, model.predict(X), color='blue', linewidth=2, label='Linear Regression Line')
plt.title('Linear Regression on Gold Price based on Purity')
plt.xlabel('Gold Purity')
plt.ylabel('Gold Price')
plt.legend()
plt.grid(ls='--')
plt.show()
import numpy as np
import matplotlib.pyplot as plt
# Parameters of the quadratic function
a = 400
b = 200
c = 900
# Generate random data
np.random.seed(42)
x = np.random.uniform(0, 1, 150)
y = a * x**2 + b * x + c + np.random.normal(0, 15, 150)
y = y.reshape(y.shape[0], 1) # Reshaping y to fit the required shape
# Create the feature matrix X
X = np.vstack((x, np.ones(len(x)))).T
# Initialize the theta parameters for the linear model
theta = np.random.randn(2, 1)
# Define the linear model function
def model(X, theta):
return X.dot(theta)
# Define the cost function
def cost_function(X, y, theta):
m = len(y)
return 1 / (2 * m) * np.sum((model(X, theta) - y)**2)
# Define the gradient calculation function
def grad(X, y, theta):
m = len(y)
return 1 / m * X.T.dot(model(X, theta) - y)
# Define the gradient descent function
def gradient_descent(X, y, theta, learning_rate, n_iterations):
cost_history = np.zeros(n_iterations)
for i in range(n_iterations):
theta = theta - learning_rate * grad(X, y, theta)
cost_history[i] = cost_function(X, y, theta)
return theta, cost_history
# Define the learning rate and number of iterations
learning_rate = 0.2
n_iterations = 20
# Perform gradient descent to optimize the parameters
theta_final, cost_history = gradient_descent(X, y, theta, learning_rate, n_iterations)
# Make predictions with the optimized parameters
predictions = model(X, theta_final)
# Plot the data points and the linear model predictions
plt.scatter(x, y, c='r',label='Data Points')
plt.plot(x, predictions, c='blue',label='Linear Regression Line')
plt.xlabel('Gold Purity')
plt.ylabel('Gold Price')
plt.title('Linear Regression on Gold Price and Gold Purity')
plt.legend()
plt.grid(ls='--')
plt.show()
# Plot the cost history during gradient descent
plt.plot(range(n_iterations), cost_history)
plt.xlabel('Number of Steps')
plt.ylabel('Descent')
plt.title('Descent History during Gradient Descent')
plt.grid(ls='--')
plt.show()
# Calculate the coefficient of determination (R-squared)
def coef_determination(y, pred):
u = ((y - pred)**2).sum()
v = ((y - y.mean())**2).sum()
return 1 - u / v
# Print Final theta
print(theta_final)
# Print the R-squared value
print(coef_determination(y, predictions))
# Display the first 5 samples of the data
print("First 5 samples of the data:")
for i in range(5):
print(f"Sample {i + 1} - Gold Purity: {x[i]:.4f}, Gold Price: {y[i][0]:.4f}")
import numpy as np
import matplotlib.pyplot as plt
# Parameters of the quadratic function
a = 400
b = 200
c = 900
# Generate random data
np.random.seed(42)
x = np.random.uniform(0, 1, 150)
y = a * x**2 + b * x + c + np.random.normal(0, 15, 150)
y = y.reshape(y.shape[0], 1) # Reshaping y to fit the required shape
# Create the feature matrix X
X = np.vstack((x**2,x, np.ones(len(x)))).T
print(X.shape)
# Initialize the theta parameters for the linear model
theta = np.random.randn(3, 1)
# Define the polynomial model function
def model(X, theta):
return X.dot(theta)
# Define the cost function
def cost_function(X, y, theta):
m = len(y)
return 1 / (2 * m) * np.sum((model(X, theta) - y)**2)
# Define the gradient calculation function
def grad(X, y, theta):
m = len(y)
return 1 / m * X.T.dot(model(X, theta) - y)
# Define the gradient descent function
def gradient_descent(X, y, theta, learning_rate, n_iterations):
cost_history = np.zeros(n_iterations)
for i in range(n_iterations):
theta = theta - learning_rate * grad(X, y, theta)
cost_history[i] = cost_function(X, y, theta)
return theta, cost_history
# Define the learning rate and number of iterations
learning_rate = 0.2
n_iterations = 20
# Perform gradient descent to optimize the parameters
theta_final, cost_history = gradient_descent(X, y, theta, learning_rate, n_iterations)
# Make predictions with the optimized parameters
predictions = model(X, theta_final)
# Plot the data points and the polynomial regression predictions
plt.scatter(x, y, c='r', label='Data Points')
plt.plot(x, predictions, c='blue', label='Polynomial Regression Line')
plt.xlabel('Gold Purity')
plt.ylabel('Gold Price')
plt.title('Polynomial Regression on Gold Price and Gold Purity')
plt.legend()
plt.grid(ls='--')
plt.show()
# Plot the cost history during gradient descent
plt.plot(range(n_iterations), cost_history)
plt.xlabel('Number of Steps')
plt.ylabel('Descent')
plt.title('Descent History during Gradient Descent')
plt.grid(ls='--')
plt.show()
# Calculate the coefficient of determination (R-squared)
def coef_determination(y, pred):
u = ((y - pred)**2).sum()
v = ((y - y.mean())**2).sum()
return 1 - u / v
# Print Final theta
print(theta_final)
# Print the R-squared value
print(coef_determination(y, predictions))



