Battre le Maître du Jeu
Par Jordan Moles le 02 octobre, 2023

Faisons les Présentations!
Au centre de cette tablée éclectique, le Ranger se tenait, autoproclamé chef de l’équipe.
Sa mission principale était de maintenir la paix au sein du groupe, notamment entre l’Elfe et le Nain, deux individus notoirement en désaccord.
Cependant, malgré ses efforts, il était souvent submergé par le désespoir, surtout lorsque les événements tournaient mal. Le Ranger n’était pas spécialisé dans une compétence particulière, mais plutôt polyvalent.
Il avait l’habitude malheureuse de surestimer ses compétences et de tenter d’utiliser des talents qu’il ne maîtrisait pas vraiment.


À sa gauche, le Barbare occupait sa place.
C’était un colosse aux muscles saillants, arborant une épée comme prolongement de son bras puissant. La vie du Barbare se résumait à deux passions : le combat et la ripaille avec le Nain.
Il ne portait aucune affection pour la magie, qu’il considérait comme une faiblesse. Il était souvent prompt à juger les autres membres du groupe comme des mauviettes ou des lâches s’ils ne partageaient pas sa passion pour la mêlée.
De l’autre côté de la table, l’Elfe se prélassait avec une grâce naturelle. D’une beauté enchanteresse, elle semblait dépourvue de tout souci. Son caractère enjoué et insouciant contrastait fortement avec celui de ses compagnons.
Son comportement était souvent perçu comme excentrique, bien qu’elle ne semblait pas en avoir conscience.
Elle entretenait une relation tumultueuse avec le Nain, une antipathie réciproque étant devenue légendaire parmi les habitués de la taverne.


À côté du Barbare, le Nain, guerrier robuste et colérique, se préparait à entrer dans l’arène du jeu qui allait bientôt débuter. Son obsession première était l’argent, et il était prêt à tout pour remplir sa bourse, même à s’embarquer dans des aventures périlleuses avec des compagnons qu’il ne pouvait pas supporter, en particulier l’Elfe, avec qui il entretenait une relation exécrable.
Le Nain était également un expert en calculs compliqués, en particulier lorsqu’il s’agissait de répartir le butin entre les membres du groupe, prenant en compte divers critères tels que le temps passé ensemble, la dangerosité des situations, et l’expérience acquise lors des combats.
Il ne manquait jamais une occasion de savourer de bons jambons, et de brandir sa petite hache qu’il maniait avec une grande habileté.
Dans l’ombre, le Voleur, habillé de manière discrète, observait la scène. Ses yeux perçants scrutaient la prochaine bourse à dérober.
Son agilité et sa dextérité légendaires faisaient de lui un maître dans l’art du vol, mais cela signifiait aussi qu’il ne pouvait pas s’empêcher de chaparder de petites choses, même parmi ses compagnons.
Son allure sombre et sa tunique en cuir noir ne laissaient que peu de traces lorsqu’il se faufilait dans l’ombre. Ses outils de crochetage, de vol et d’espionnage étaient soigneusement dissimulés sous une ceinture discrète.


Ensuite la magicienne trônait juste à côté de l’elfe. C’était une femme aux cheveux rouge profonds passionnée par les ouvrages en tous genres qui voue une fascination particulière aux grimoires de sorts.
Malheureusement, ses talents en magie sont limités, et elle ne brille pas particulièrement dans ce domaine. Malgré son manque d’aptitude magique, elle compense par sa connaissance approfondie des livres.
Sur le plan vestimentaire, elle porte généralement une robe longue de couleur bleu foncé, ornée de motifs argentés qui rappellent des étoiles scintillantes. Sa tenue est complétée par un chapeau pointu assorti, qui ajoute une touche de mystère à son apparence. Elle porte également une ceinture en cuir avec des poches pour ranger de petits objets magiques et des composants pour ses sorts.
La Magicienne demeure une source de connaissances inestimable pour le groupe et joue un rôle central au sein de la compagnie, partageant effectivement la direction de l’équipe avec le Ranger.
Enfin, à ses coté, l’Ogre se tenait, une créature imposante. Son appétit insatiable se manifestait par des grognements primitifs. Bien qu’il soit de nature gentille, il restait une source constante de tracas, renversant des chaises et cassant des verres à intervalles réguliers.
Ses actions étaient principalement dictées par ses instincts, ce qui le rapprochait du Barbare, avec qui il partageait une passion pour la bonne chère. Cependant, il entretenait une relation spéciale avec la Magicienne, la seule capable de comprendre son langage.

Les Règles du Jeu
Après plusieurs pintes de bière, de disputes enflammées, de blagues douteuses et d’anecdotes épiques, l’atmosphère dans la taverne était à son comble. Les rires bruyants et les chants désaccordés des aventuriers avaient rempli la pièce, tandis que les serveuses débordées tentaient de satisfaire les commandes toujours plus nombreuses.
La Magicienne, échauffée par l’ambiance festive, décida que le moment était venu d’ajouter une touche d’excitation supplémentaire à la soirée. Elle sortit soudainement une série de 14 mystérieux dés de sa besace, 2 chacun, attirant immédiatement l’attention de ses compagnons. Les regards curieux se posèrent sur les dés, tandis que les conversations se calmèrent peu à peu.
Le visage illuminé par un sourire malicieux, elle annonça d’une voix claire : « Mes amis, nous allons pimenter cette soirée avec un jeu de dés ! Qui est prêt à tenter sa chance ? »
L’annonce de la Magicienne suscita une vague d’enthousiasme parmi les aventuriers déjà éméchés.
Le Nain, toujours avide d’opportunités pour gagner de l’or mais sans vouloir parier le sien, frappa la table de ses mains calleuses et s’exclama : « Par les barbes de nos ancêtres, je suis partant ! »
L’Elfe, enjouée malgré ses désaccords fréquents avec le Nain, sourit et dit : « Pourquoi pas ? Cela pourrait être amusant. »
Même l’Ogre, dont l’expression faciale limitée ne laissait pas transparaître grand-chose, émit un grognement de consentement.
Le ranger suivi du barbare et du voleur s’en allèrent vite chercher de quoi se ravitailler, planche de fromage, Jambon de pays avant d’écouter les règles du jeu attentivement.
La Magicienne, ravie de voir que son idée avait été si bien accueillie, fouille dans sa besace et sort un large parchemin. C’était les lois élémentaires qu’il fallait absolument lire avant de jouer. Elles étaient écrites d’une drôle de manière, on aurait dit des runes que seule la magicienne pouvait déchiffrer mais voici la note transcrite magiquement dans notre langage:
Cher mortel, prenez garde car je vais vous initier aux mystères profonds qui gouvernent ces dés sacrés. Ils sont soumis à des lois énigmatiques qu’il vous faut comprendre avant de les libérer sur la table. Suivez mes paroles avec attention, et vous découvrirez le pouvoir caché derrière chaque lancer. Voici la plus importante, celle qui les définies toutes
Soit (\(\Omega\), A) un espace mesurable, où \(\Omega\) est l’univers et A est une tribu. Une loi de probabilité est une mesure dont la masse totale vaut 1 et vérifie les trois axiomes suivants:
• Pour tout ensemble E dans A, la probabilité \(\mathbb{P}\)(E) est un nombre réel compris entre 0 et 1.
• La probabilité de l’univers \(\Omega\) est égale à 1, c’est-à-dire \(\mathbb{P}(\Omega) = 1\).
• La probabilité est \(\sigma\)-additive, ce qui signifie que pour toute famille finie ou dénombrable d’ensembles deux à deux disjoints \((E_i, i \in I)\) de A, la probabilité de leur réunion est égale à la somme des probabilités individuelles :
\begin{equation*}\mathbb{P}\left(\bigcup_{i\in I} E_i\right) = \sum_{i\in I} \mathbb{P}(E_i)\end{equation*}
En particulier, la probabilité de l’ensemble vide (\(\emptyset\)) est égale à 0, c’est-à-dire \(\mathbb{P}(\emptyset) = 0\).
L’Elfe, le Barbare et le Ranger se grattent la tête en signe de confusion, tandis que le Nain, toujours attentif à la perspective de gagner de l’or, acquiesce en silence. La Magicienne, voyant que ses explications n’ont pas été comprises par tous, décide de simplifier davantage.
Elle sort un petit morceau de papier de sa poche et commence à expliquer de manière plus concise : « D’accord, oublions les termes compliqués. L’univers, c’est simplement tous les résultats possibles. Par exemple, lorsque nous lançons un dé, les résultats possibles sont 1, 2, 3, 4, 5 et 6. C’est l’univers, que nous notons \(\Omega=\{1, 2, 3, 4, 5, 6\}\).
Ensuite, une tribu, c’est l’ensemble de tous les sous-ensembles de l’univers, c’est-à-dire tous les groupes possibles de résultats que nous pouvons obtenir. Par exemple, un sous-ensemble pourrait être l’ensemble des nombres pairs, c’est-à-dire \(\{2, 4, 6\}\). Comprenez-vous jusqu’ici ?
Passons aux axiomes. Le premier est simple : il dit juste que la probabilité d’un événement est toujours entre 0 et 1. En d’autres termes, cela signifie que la probabilité d’obtenir un résultat est toujours soit nulle (impossible) ou un (certain).
Le deuxième axiome est encore plus simple. Il dit que la probabilité totale de tous les résultats possibles est toujours de 1. Donc, si nous ajoutons la probabilité d’obtenir chaque nombre de notre dé, elle doit toujours être égale à 1.
Le troisième axiome, un peu plus complexe, signifie que si nous avons deux événements qui ne peuvent pas se produire en même temps (disjoints), alors la probabilité que l’un ou l’autre se produise est simplement la somme des probabilités de chacun. Par exemple, la probabilité d’obtenir un 1 ou un 6 en lançant un dé équilibré est la somme de la probabilité d’obtenir un 1 et la probabilité d’obtenir un 6.
J’espère que cela clarifie un peu les choses ! »
La Magicienne, consciente que ses compagnons commencent à s’impatienter avec les termes techniques, décide de simplifier davantage les explications pour rendre les concepts plus accessibles.
Elle poursuit son récit : « Maintenant, oublions un instant les termes complexes. Les lois de probabilité peuvent être décrites en trois grandes catégories de caractéristiques comme indiqué sur ce parchemin: »
•«Il y a les paramètres de position qui influencent la tendance centrale de la loi de probabilité. Ils déterminent les valeurs autour desquelles la probabilité est la plus concentrée c’est à dire ou la plupart des résultats se regroupent. Parmi ces paramètres, on trouve l’espérance qui est une mesure de moyenne, la médiane qui est la valeur centrale, et le mode qui est la valeur la plus fréquente. »
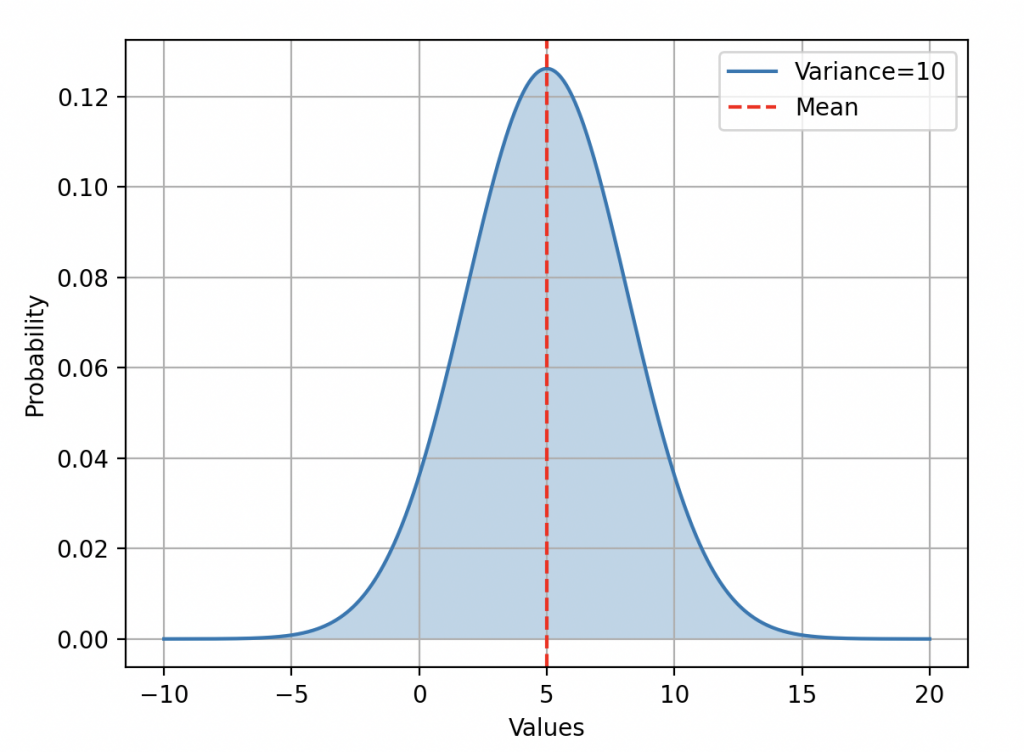
Loi de distribution normale de moyenne égale à 5 et de variance égale à 10.

• « Ensuite, il y a les paramètres d’échelle. Ils mesurent à quel point les valeurs sont étalées ou serrées autour de ces valeurs centrales. La variance, l’écart type et l’écart interquartile sont des exemples de ces paramètres. Nous nous intéresserons souvent à la variance qui fonctionne comme ceci:
Si elle est proche de zéro, cela suggère que les valeurs individuelles sont similaires et se regroupent étroitement autour de la moyenne.
En revanche, une variance élevée indique que les valeurs individuelles sont plus éloignées de la moyenne, avec une plus grande dispersion globale. »


Deux lois de distribution normale de moyenne égale à 5 et de variance égale à 2 et l’autre à 20.
• « Enfin, nous avons les paramètres de forme. Ils décrivent la manière dont les probabilités changent à mesure que l’on s’éloigne des valeurs centrales.
Par exemple, l’asymétrie mesure si la distribution est inclinée d’un côté ou de l’autre, et le kurtosis ou coefficient d’aplatissement examine à quel point les valeurs sont concentrées près de la moyenne. »

Loi de distribution normale d’asymétrie nulle et une loi de distribution normale d’asymétrie égale à 10.

La Loi du dé
La Magicienne marque une pause, avant de conclure : « Maintenant que nous avons survolé ces concepts, plongeons dans le cœur du sujet qui semble vous intéresser : la loi de probabilité uniforme discrète. »
Elfe : (en chuchotant au barbare) Ah, il est pas trop tôt, c’est bientôt l’heure d’aller dormir.
Barbare : (riant discrètement) Ouais, j’espère que ce cours magistral va se terminer avant minuit.
Ranger : (en souriant) Peut-être qu’on devrait préparer des couvertures pour nos camarades fatigués.
La Magicienne, les regardant d’un air amusé, décide de continuer malgré les remarques taquines de ses compagnons.
Magicienne : La loi uniforme discrète est peut-être la loi de probabilité la plus importante que vous devez comprendre ici. Elle garantit l’équiprobabilité, ce qui signifie que chaque réalisation a une probabilité identique pour chaque modalité d’un ensemble fini de modalités possibles.
Le nain perds patience fasse à tant de jargon et arrache le parchemin des mains de la magicienne.
Nain : (fronce les sourcils) Attendez une seconde… ce vieux parchemin dit que je devrais vous donner une pièce d’or ? Je ne suis pas sûr de comprendre pourquoi je devrais faire ça.
Barbare : (riant) Haha ! Le parchemin prédit l’avenir ! Allez, donne-lui la pièce, nain !
Le nain refuse de donner sa pièce, mais le barbare, impatient, lui donne un coup de poing sur la tête.
Barbare : (riant) Allez, nain, fais-le pour l’éducation ! Ça ne coûte qu’une pièce.
L’Ogre: (met un grand coup sur la table en riant), Zog zog.
L’elfe : bien fait.
Le nain, légèrement sonné par le coup, finit par remettre une pièce d’or à contrecœur à la Magicienne et le parchemin.
Magicienne : Parfait, merci pour votre contribution. Donc, pour mieux comprendre, imaginez une pièce de monnaie équilibrée. Lorsque vous la lancez, chaque face a la même chance d’apparaître, soit 1/2.
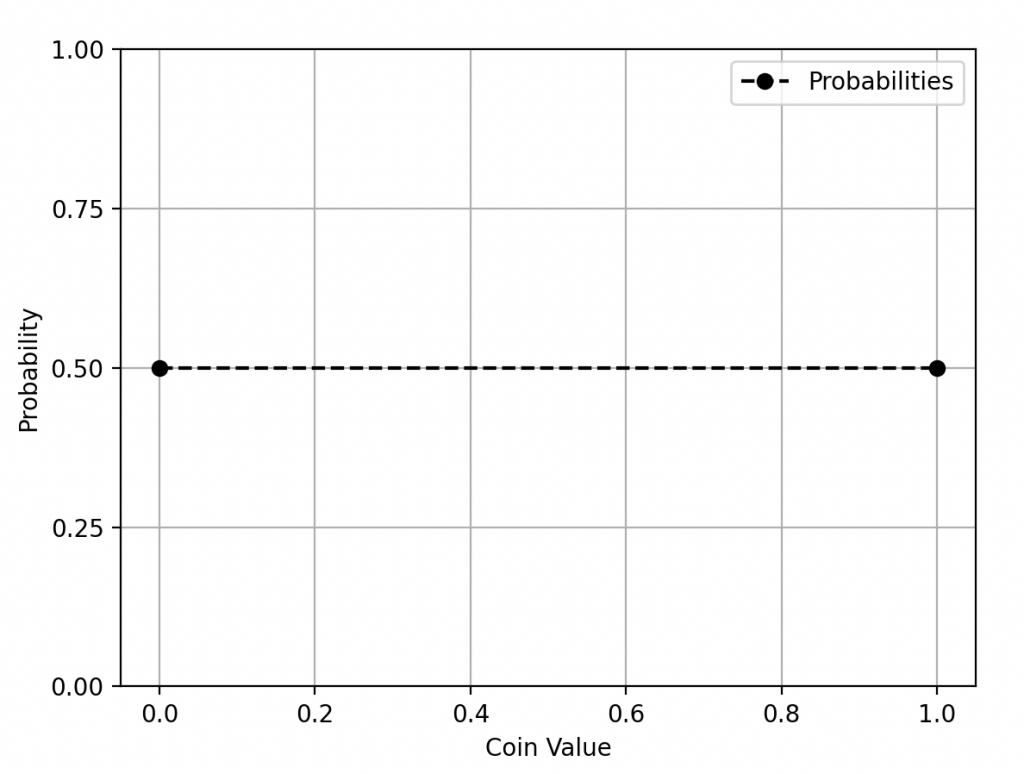
Loi de probabilité uniforme discrète à deux modalités (Lancer de pièce).

Pour mes dés, c’est la même chose. Un dé classique possède 6 faces, ce qui correspond à 6 modalités, et s’il est équilibré on dit qu’elles sont toutes équiprobables.

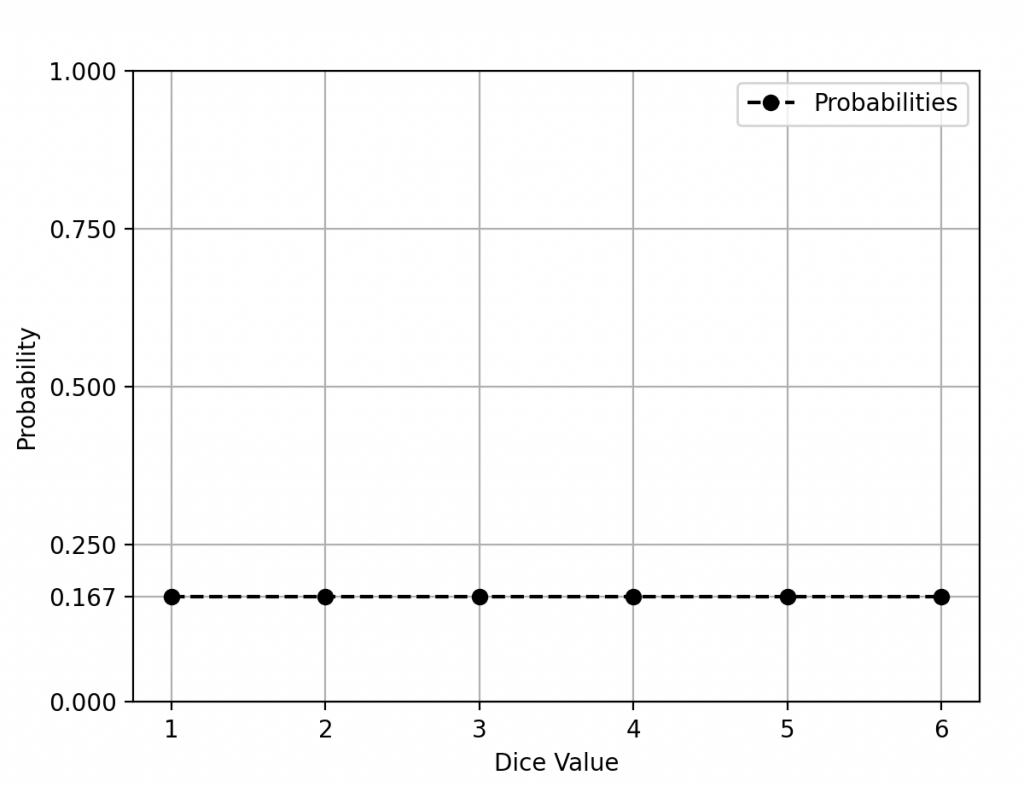
Loi de probabilité uniforme discrète à six modalités (Lancer de dé).
Le voleur : (d’un air curieux) Montre-moi cette pièce, j’aimerais l’examiner de plus près pour mieux comprendre le pile ou face.
Magicienne : (lui tendant la pièce) Bien sûr, voici la pièce. Elle est équilibrée, donc chaque face a une chance égale de tomber.
Elfe : (levant la main) Attendez, pour le dé, on peut dire quoi de plus ?
Magicienne : (souriant) Plein de choses, voici les principales caractéristiques de ces dés :
On appelle \(X\) la variable aléatoire qui suit la loi uniforme discrète (le jet de dé)
• L’espérance : c’est comme la moyenne, et pour un dé classique, c’est \(\mathbb{E}(X)= \frac{6+1}{2}=3,5\)
• La médiane : c’est la valeur centrale, également \(m(X)= \frac{6+1}{2}=3,5\) pour un dé équilibré
• Le mode : il n’y en a pas ici, car chaque face a la même probabilité d’apparaître.
•La variance : elle mesure la dispersion des résultats, et pour un dé équilibré, elle est d’environ \(V(X)=\frac{6^{2}-1}{12}\approx2.91\)
• L’asymétrie est nulle, et le kurtosis…
Ranger : (l’interrompant) Excusez-moi, mais ça suffit pour les règles, non ? On a compris l’essentiel.
La Magicienne: Bon, mais il reste encore deux, trois lois dans ce parchemin, la loi de probabilité triangulaire, la loi ….
Nain : (grincheux) Bon sang, on est pas venus ici pour faire des cours de mathématiques ! On veut lancer ces dés et jouer, pas écouter des discours interminables.
Barbare : (tapant sur la table) Il a raison, tout ça, c’est bien joli, mais on veut de l’action, pas des chiffres !
Le voleur : (en observant la pièce de près) Ouais, je suis d’accord avec eux. On pourrait commencer à jouer maintenant, non ?
Le nain: Rend moi ma pièce!
Magicienne : (tentant de garder son calme) D’accord, d’accord, je vois que vous êtes tous très impatients. Mais avant de lancer les dés, laissez-moi juste jeter un dernier coup d’œil à cette note en bas de page. Je veux m’assurer que nous suivons bien toutes les règles.
La magicienne commence à lire rapidement la note en bas de page, mais soudain, elle s’arrête net.
Magicienne : (surprise) Attendez, il y a quelque chose d’important ici que je n’avais pas remarqué ! Il est écrit : « Ne lancez pas la pièce avant de jouer aux dés, car… »
Avant qu’elle puisse finir sa phrase, le voleur envoie la pièce d’or en l’air pour la rendre au nain. Mais au lieu de retomber dans sa main, la pièce commence à virevolter dans les airs de manière mystérieuse, émettant une lueur magique.
Nain : (surpris) Par les barbes de nos ancêtres, qu’est-ce qui se passe ?
La pièce continue de tournoyer dans les airs, de plus en plus rapidement, et soudain, elle disparaît complètement, laissant tout le monde perplexes.
Elfe : (étonné) Où est passée la pièce ?
Magicienne : (choquée) Je… Je ne sais pas. Il semblerait que les dés soient plus mystérieux que je ne le pensais.
Barbare : (excité) Quoi qu’il en soit, ça a l’air amusant ! Laissez-nous lancer les dés maintenant !
Le nain: (énervé) ou est ma pièce ?
C’était une soirée de beuverie, de paris audacieux et de tumulte dans la vieille auberge. Les aventuriers avaient fait halte pour se détendre après une longue journée d’exploration et, comme à leur habitude, ils s’étaient laissés emporter par l’excitation de la soirée.
Le Nain, déjà de mauvaise humeur, décida que tout était toujours la faute de l’Elfe. Il avait pris l’Elfe comme bouc émissaire, lui attribuant la responsabilité de tous les maux du groupe, répétant sans cesse que « c’était à cause de l’Elfe que tout tournait mal ». Cette attitude exécrable ne faisait qu’empirer à mesure que la soirée progressait.
Pendant qu’ils jouaient aux dés et pariaient de l’argent, le Voleur avait décidé de pimenter la soirée en volant discrètement la culotte d’une serveuse. C’était un acte aussi audacieux que risqué, mais il avait réussi à accomplir cette prouesse avec une dextérité remarquable.
Le Barbare, quant à lui, avait laissé libre cours à son impulsivité en frappant le vigile à l’entrée de l’auberge après une dispute mineure. Le vigile n’avait pas tardé à appeler des renforts qui avait calmé le barbare à grand coup de matraque. Ce qui avait plongé le groupe dans une situation encore plus compliquée
L’Ogre, toujours affamé et curieux, avait décidé de satisfaire son appétit en avalant une boule de billard. Cela avait provoqué un grand éclat de rire parmi les clients de l’auberge, mais aussi beaucoup d’inquiétude quant à l’état de santé de l’Ogre.
Enfin, le Nain, complètement ivre, avait fini par vomir sa bière sur le tenancier de l’auberge, provoquant ainsi une bagarre générale entre les aventuriers et les autres clients.
Le chaos qui s’ensuivit ne pouvait que mener à une seule conclusion inévitable : tous les aventuriers se retrouvèrent finalement au cachot, où ils allaient devoir faire face à de nouvelles péripéties pour s’échapper de cette mauvaise passe. C’était le début d’une aventure qui allait les entraîner bien plus loin que ce qu’ils avaient pu imaginer lors de cette soirée de débauche et de désordre.
Le Donjon
Le ranger, connu pour sa sagesse (du moins, il le prétendait), rassembla le groupe hétéroclite d’aventuriers dans un coin sombre de leur cellule crasseuse. La faible lueur d’une torche vacillante ajoutait une ambiance pittoresque à leur situation déjà pas très reluisante.
« Écoutez-moi, compagnons, » commença le ranger d’une voix ferme, mais qui trahissait une certaine nervosité. « Nous sommes dans une situation critique, mais nous ne sommes pas n’importe qui. Nous formons une troupe d’élite, et nous ne pouvons pas nous résoudre à rester enfermés ici comme de vulgaires rats dans un égout. Ce dont nous avons besoin, c’est d’un plan. »
Là-dessus, l’elfe et le nain commencèrent à se disputer comme des gamins, se traitant mutuellement de « suceurs de lichen » et de « mangeurs de cailloux ». Le nain, ayant la peau plus épaisse que l’elfe (littéralement), rétorqua en insultant les oreilles pointues de l’elfe et en lui suggérant de retourner jouer de la flûte dans la forêt.
Le barbare, qui avait l’air de s’ennuyer ferme, interrompit la querelle et décida de se servir de sa force herculéenne pour enfoncer la porte. Malheureusement, lors de l’arrestation il a reçu un violent coup sur la tête et est encore hébété par le choc.
Le Maître du Jeu lui demande d’effectuer son jet de dé en situation de désavantage, ce qui signifie qu’il tirera 2 fois le dé et ne gardera que le résultat le plus défavorable. De plus, la porte est en acier, faite pour encaisser les efforts de prisonniers voulant se soustraire à leur sentence.
Sélectionnez:
Number of dice = 1
Type of dice = 6
Lancez deux fois le dé et sélectionnez le plus petit résultat.
Number of dice
Type of die:
Modifier
Result:

Bibliographie
P. Barbé et M. Ledoux, Probabilité, Les Ulis, EDP Sciences, 2007.
P. Bogaert, Probabilités pour scientifiques et ingénieurs : Introduction au calcul des probabilités, Paris, Éditions De Boeck, 2006.
M. Lejeune, Statistique : la théorie et ses applications, Springer Science et Business Media, 2004.
F. Caravenna, P. Dai Pra et Q. Berger, Introduction aux probabilités : Modèles et applications : mathématiques, physique, informatique, sciences de l’ingénieur, biologie, Dunod, 1er septembre 2021.
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import norm
# Parameters for normal distributions
mean = 5 # Common mean for both distributions
variance1 = 10 # Variance for the first example
variance2 = 20 # Variance for the second example
# Generate data for the two distributions
x = np.linspace(-10, 20, 1000)
pdf1 = norm.pdf(x, loc=mean, scale=np.sqrt(variance1))
pdf2 = norm.pdf(x, loc=mean, scale=np.sqrt(variance2))
# Plot probability density functions with transparent fill color
plt.plot(x, pdf1, label=f'Variance={variance1}')
plt.fill_between(x, pdf1, alpha=0.3)
#plt.plot(x, pdf2, label=f'Variance={variance2}')
#plt.fill_between(x, pdf2, alpha=0.3)
# Calculate the mean for both cases (they should be equal)
mean1 = mean
mean2 = mean
# Draw vertical lines for the means
plt.axvline(x=mean1, color='r', linestyle='--', label=f'Mean')
plt.xlabel('Values')
plt.ylabel('Probability')
plt.legend()
plt.grid(True)
plt.show()
print(f"Mean (Var={variance1}): {mean1:.2f}")
print(f"Mean (Var={variance2}): {mean2:.2f}")
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import norm
# Parameters for normal distributions
mean = 5 # Common mean for both distributions
variance1 = 10 # Variance for the first example
variance2 = 20 # Variance for the second example
# Generate data for the two distributions
x = np.linspace(-10, 20, 1000)
pdf1 = norm.pdf(x, loc=mean, scale=np.sqrt(variance1))
pdf2 = norm.pdf(x, loc=mean, scale=np.sqrt(variance2))
# Plot probability density functions with transparent fill color
plt.plot(x, pdf1, label=f'Variance={variance1}')
plt.fill_between(x, pdf1, alpha=0.3)
plt.plot(x, pdf2, label=f'Variance={variance2}')
plt.fill_between(x, pdf2, alpha=0.3)
# Calculate the mean for both cases (they should be equal)
mean1 = mean
mean2 = mean
# Draw vertical lines for the means
plt.axvline(x=mean1, color='r', linestyle='--', label=f'Mean')
plt.xlabel('Values')
plt.ylabel('Probability')
plt.legend()
plt.grid(True)
plt.show()
print(f"Mean (Var={variance1}): {mean1:.2f}")
print(f"Mean (Var={variance2}): {mean2:.2f}")
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import skewnorm
# Parameters for the normal distribution
mean1 = 5
std_dev1 = 2
skewness1 = 0
# Parameters for the asymmetric normal distribution
mean2 = 5
std_dev2 = 2
skewness2 = 10 # Positive skewness (right-skewed)
# Create a range of x values
x = np.linspace(0, 10, 1000)
# Calculate the probability density functions (PDFs) for both distributions
pdf1 = skewnorm.pdf(x, skewness1, loc=mean1, scale=std_dev1)
pdf2 = skewnorm.pdf(x, skewness2, loc=mean2, scale=std_dev2)
# Plot the PDFs as curves
plt.plot(x, pdf1, label=f'Skewness={skewness1}')
plt.fill_between(x, pdf1, alpha=0.3)
plt.plot(x, pdf2, label=f'Skewness={skewness2}')
plt.fill_between(x, pdf2, alpha=0.3)
plt.xlabel('Values')
plt.ylabel('Probability')
plt.legend()
plt.grid(True)
plt.show()
import matplotlib.pyplot as plt
# Define possible values (coin faces)
values = [0, 1]
# Calculate uniform probabilities (each face has a 1/2 probability)
probabilities = [1/2] * 2
# Set the values to display on the y-axis
plt.yticks([0, 0.25, 1/2, 0.75, 1])
# Create the scatter plot
plt.plot(values, probabilities, marker='o', color='black', label='Probabilities', ls='--')
# Limit the y-axis scale from 0 to 1
plt.ylim(0, 1)
# Label the axes and add a title
plt.xlabel('Coin Value')
plt.ylabel('Probability')
# Display the plot
plt.grid(True)
plt.legend(loc='upper right')
plt.show()
import matplotlib.pyplot as plt
# Define possible values (dice faces)
values = [1, 2, 3, 4, 5, 6]
# Calculate uniform probabilities (each face has a 1/6 probability)
probabilities = [1/6] * 6
# Create the scatter plot
plt.plot(values, probabilities, marker='o', color='black', label='Probabilities', ls='--')
# Set the values to display on the y-axis
plt.yticks([0, 1/6, 0.25, 0.5, 0.75, 1])
# Label the axes and add a title
plt.xlabel('Dice Value')
plt.ylabel('Probability')
# Display the plot
plt.grid(True)
plt.legend(loc='upper right')
plt.show()

