Comment Construire son Hôte ?
Episode I
Par Jordan Moles le 2 Janvier, 2024

En l’an 2051, un groupe de jeunes scientifiques chanceux se voit offrir l’opportunité exclusive d’explorer les arcanes de WestWorld. Leur voyage dans les coulisses prend une tournure exceptionnelle alors qu’ils sont conviés à une conférence unique, orchestrée par le directeur énigmatique du parc, le Dr. Ford. Au cœur de cette rencontre, une plongée fascinante dans le monde du Deep Learning réserve aux participants une expérience inédite, dévoilant les secrets de la symbiose entre la technologie de pointe et l’imagination audacieuse de WestWorld.
Aux Confins de l'Intelligence
Bienvenue, esprits novateurs, dans WestWorld, un parc d’attractions révolutionnaire où l’innovation technologique et l’audace artistique fusionnent pour créer une expérience immersive sans précédent. Je suis le Dr.Ford et en tant que Directeur de ce parc d’un genre nouveau, je suis ici pour vous dévoiler les rudiments computationels et la vision mathématique qui sous-tendent ce projet extraordinaire.


Notre ambition va bien au-delà d’une simple récréation de l’Ouest sauvage. WestWorld repousse les limites de l’imagination en introduisant des hôtes, des androïdes d’une sophistication inégalée, capables d’interagir de manière indiscernable avec nos visiteurs. Ce n’est pas simplement un divertissement ; c’est une exploration des recoins les plus profonds de l’intelligence artificielle: le Deep Learning.
Au cœur de ce paradis forgé par la technologie, notre quête vise à repousser sans cesse les frontières du possible. Nos hôtes ne se bornent pas à reproduire des actions préprogrammées ; ils réagissent, apprennent et évoluent en temps réel. Nourris pendant des années par une imposante base de données, nous les avons entraînés, validés et soumis à des tests (apprentissage supervisé), assurant ainsi qu’ils offrent une expérience unique et aient la capacité d’apprendre de manière autonome par la suite.
Les réseaux de neurones qui les alimentent, s’inspirant de la complexité du cerveau humain, les dotaient de la polyvalence nécessaire pour accomplir une variété de tâches, de la conduite d’une charrette à la montée à cheval, de la lecture à l’écriture, de la reconnaissance de leurs semblables à l’expression de l’empathie via la reconnaissance d’émotions. Cette union sublime entre la machine et la pensée humaine va bien au-delà des modèles classiques de Machine Learning tels que les K-Nearest Neighbors, les arbres de décision ou les machines à vecteurs de support. Chaque interaction avec un visiteur représente une occasion d’affiner leurs compétences cognitives (apprentissage non supervisé), offrant ainsi une expérience unique à chaque instant, même si cet aspect ne sera pas exploré dans cette conférence.

Au Commencement: Le neurone biologique
Au nombre d’environ 86 milliards et connectées par des milliers voire des dizaines de milliers de synapses, ces cellules hautement spécialisées, inscrites dans notre patrimoine génétique depuis des milliards d’années, sont appelées neurones.
Assemblés en réseau, ces neurones que nous qualifions de « biologiques » par opposition à « artificiels » génèrent la pensée humaine et ce que nous qualifions d’intelligence. Cependant, ils ne sont pas les seules cellules cérébrales en action. D’autres types cellulaires jouent un rôle fondamental et contribuent au processus neuronal, leur présence essentielle étant indispensable à l’existence même des neurones.
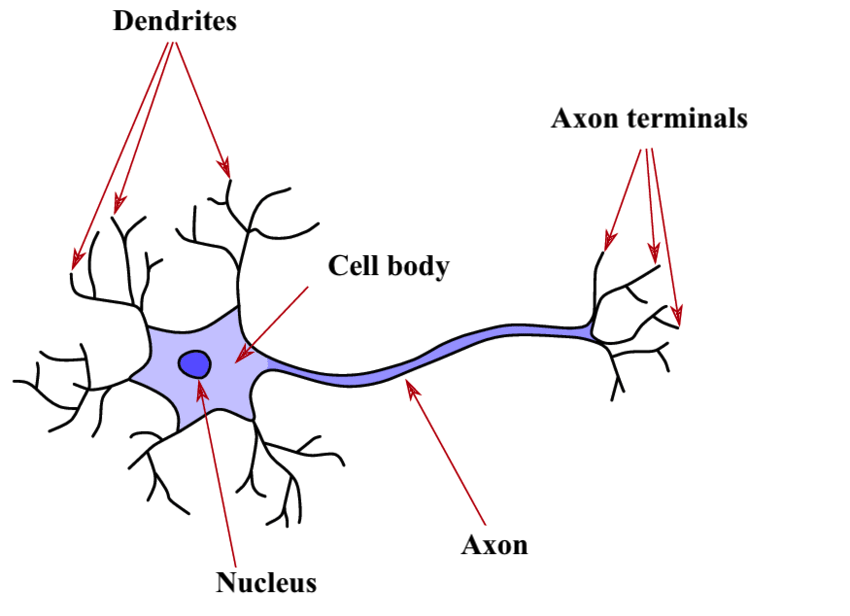
Sa Structure
Les dendrites agissent comme des interfaces avec l’environnement, formant l’entrée du neurone. En grand nombre, ces prolongements réagissent à divers stimuli, tels que la lumière au niveau des yeux ou la pression sur la peau, générant des décharges électriques, également appelées potentiels d’action, dirigées vers le corps cellulaire. La synapse, point de connexion entre les neurones, joue un rôle essentiel à cet endroit, où le neurone reçoit des signaux des neurones précédents ou de l’extérieur. Ces signaux, qu’ils soient inhibiteurs ou excitateurs (+1 ou -1), convergent vers le neurone, et lorsque leur somme dépasse un seuil critique, le neurone s’active, produisant ainsi un signal électrique.
Le corps cellulaire, central dans le processus, effectue une sommation de l’intensité des influx électriques provenant de toutes les dendrites. Si cette somme dépasse un seuil critique, le neurone s’active et génère une décharge électrique transmise à l’axone, la voie de sortie unique du neurone. Ce seuil critique, déterminant l’excitation supra-liminaire, revêt une importance cruciale.
L’axone, en tant que voie finale commune, se ramifie en multiples extensions, connectant le neurone à d’autres neurones par le biais des dendrites et des synapses suivants. Ces points de connexion, représentés anatomiquement comme des fentes synaptiques, sont essentiels pour le transfert d’informations entre les neurones. La terminaison de l’axone, marquée par des vésicules de neurotransmetteurs, libère ces messagers chimiques dans la fente synaptique. En retour, la dendrite du neurone suivant, équipée de récepteurs, fixe les neurotransmetteurs, déclenchant ainsi la formation d’un courant électrique au niveau de la dendrite.
Le message En ce qui concerne l’information transmise par le neurone, il est crucial de comprendre son dualisme électrochimique. Initialement créée sous forme électrique au niveau des dendrites en réponse à un stimulus, l’information se propage à travers le corps cellulaire vers l’axone. À la terminaison de celui-ci, l’influx électrique déclenche la libération de neurotransmetteurs, transformant l’information en une forme chimique à la synapse.

Son fonctionnement
Pivot du système nerveux, il se révèle ainsi comme la cellule maîtresse capable de transmettre des signaux électrochimiques à travers tout l’organisme. Ces signaux, résultant de dépolarisations de la membrane plasmique et de la libération de molécules chimiques aux points de connexion avec d’autres cellules, forment le fondement de la neurotransmission.
Chaque neurone, dédié à des tâches spécifiques, contribue à un réseau complexe qui permet d’accomplir des fonctions aussi diverses que la mémorisation, la motricité, la facilité d’apprentissage ou encore la reconnaissance vocale etc.
La variété des neurones, reflétant la diversité des rôles qu’ils remplissent, en fait les acteurs essentiels dans l’orchestration complexe des fonctions du système nerveux. Ces cellules, par leurs prolongements, les dendrites et l’axone, établissent des connexions vitales avec les organes innervés et d’autres neurones, consolidant ainsi leur rôle central dans les fonctions du système nerveux.
Le Premier Neurone Artificiel de l'Histoire
Chers auditeurs, il est maintenant opportun de vous présenter le célèbre neurone artificiel, un concept majeur en informatique inauguré par W. McCulloch et W. Pitt dès 1943, une époque déjà bien révolue.
Bien que dépourvu de réalité physique, ce remarquable élément offre une réplique algorithmique simple de son homologue biologique, marquant ainsi le début d’une fascinante aventure dans le monde de l’intelligence artificielle.
Sa Structure et son Fonctionnement
La structure du neurone artificiel est caractérisée par plusieurs éléments clés, notamment l’entrée et les poids synaptiques, le corps cellulaire, et la sortie. Chacun de ces aspects contribue de manière cruciale au traitement de l’information au sein des réseaux de neurones artificiels. Voyons tout cela en détail.
On Recueille l'Information
Commençons par l’entrée. En informatique, l’entrée représente les données à traiter, à l’instar d’une suite de caractère, d’une image, de densité d’or ou même de vidéo.
Chaque neurone artificiel reçoit un nombre variable d’entrées provenant de neurones amonts que nous noterons X. Ces entrées sont les signaux qui activent le neurone et seront accompagnées de poids (représentés par « w » pour « weight ») qui quantifient la force de la connexion.
L’ensemble de ces entrées forme la première étape du traitement de l’information par le neurone artificiel.

Le Corps Cellulaire Artificiel: une Fonction Mathématique
La phase d’agrégation. Des poids synaptiques, inspirés du fonctionnement des dendrites, sont attribués à chaque valeur d’entrée représentant l’importance relative des différentes connexions pour le neurone puis on somme les entrées ainsi pondérées en ajoutant un biais (une valeur constante). Pour le moment on considère seulement des poids synaptiques valant +1 (excitateur) ou -1 (inhibiteur) mais plus tard nous généraliserons.
La phase d’activation. Une fonction d’activation détermine ensuite si le neurone doit être activé ou pas. On choisi d’abord une fonction seuil (que l’on nomme Heaviside), c’est à dire une fonction qui retourne une sortie y=1 si la somme pondérées précédente dépasse une valeur seuil et 0 sinon (en voici une représentation).
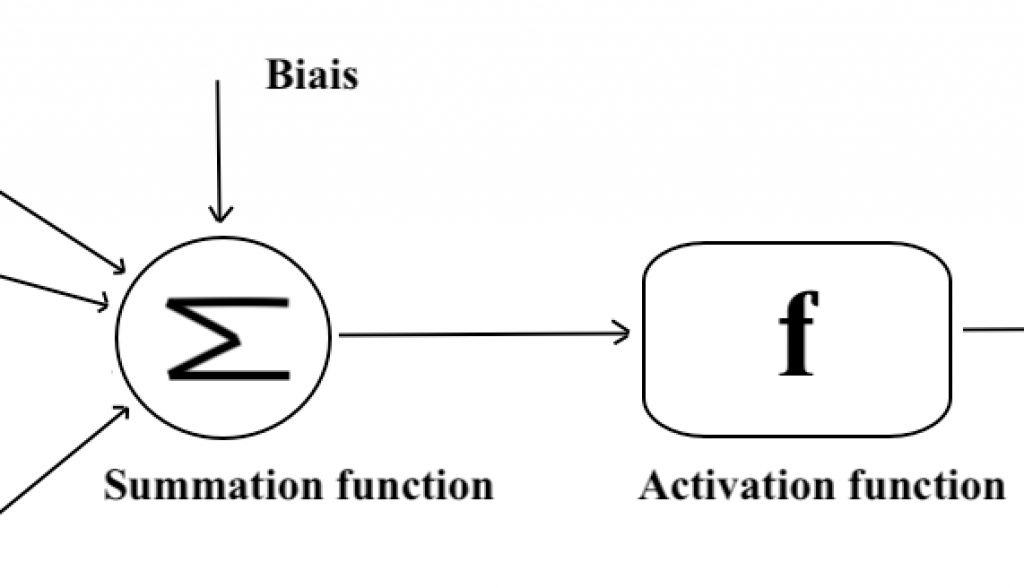
Les fonctions d’activation sont cruciale dans le traitement de l’information et peuvent prendre différentes formes, telles que la fonction seuil, la fonction sigmoïde (vous vous souvenez de la sigmoïde), la fonction de seuil rectifié linéaire (ReLU) ou même tangente hyperbolique.

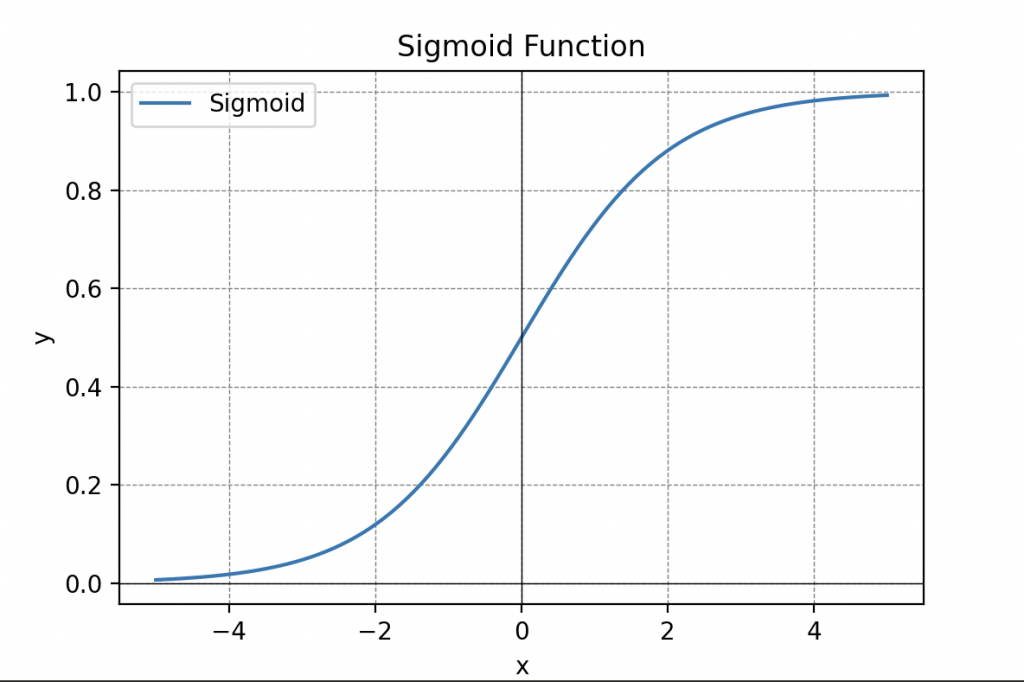


Information Traitée
La sortie du neurone artificiel est le résultat final du traitement de l’information contenu dans les données d’entrée X soit y=0 (activé) soit y=1 (désactivé). Elle peut être transmise à d’autres neurones, formant ainsi une chaîne complexe de calculs qui caractérise le fonctionnement global du réseau de neurones artificiels.



Ce premier modèle de neurone artificiel a été ultérieurement désigné sous le nom de « Threshold Logic Unit » en raison de sa capacité à traiter uniquement des entrées logiques valant soit 0, soit 1. Ils ont réussi à démontrer que ce modèle était apte à reproduire certaines fonctions logiques telles que les portes ET et OU (respectivement AND et OR en anglais). De plus, en interconnectant plusieurs de ces fonctions de manière similaire aux connexions entre les neurones de notre cerveau, il semblait possible de résoudre pratiquement n’importe quel problème de logique booléenne.
Malgré l’engouement démesuré suscité par cette annonce, je tiens à vous assurer que, à l’époque, une part significative communauté scientifique pensait que nous pourrions développer des intelligences artificielles capables de remplacer entièrement les êtres humains.
Scientifique de l’audience en regardant les hôtes à côté du Dr. Ford: « Ils n’avaient pas totalement tords ! » Rires dans la salle.
Dr Ford reprend avec le sourire: En effet, pas totalement, juste que leur échelle de temps n’était pas adapté à cette annonce. Toujours est il que cette anticipation ne s’est pas concrétisée directement. Bien que ce modèle ait jeté les bases de ce qui est aujourd’hui le Deep Learning, il présente plusieurs lacunes, notamment l’absence d’un algorithme d’apprentissage. Ainsi, il revient à l’utilisateur de déterminer manuellement les valeurs des paramètres « W » s’il souhaite appliquer ce modèle à des applications du monde réel.
Un Exemple Simple
Normalement c’est les bases, mais commençons par une explication succincte de l’algèbre booléenne pour les deux scientifiques du fond.
L’algèbre de Boole, nommée d’après le mathématicien britannique George Boole, constitue une branche des mathématiques se focalisant sur la représentation et la manipulation de l’information logique par le biais d’opérations sur des variables appelées booléennes. Ces variables ne peuvent prendre que deux valeurs, généralement notées 0 et 1, symbolisant respectivement les états faux (non) et vrai (oui).
Largement utilisée en informatique, en électronique et dans d’autres domaines liés au traitement de l’information, l’algèbre de Boole est fondamentale pour la conception des circuits logiques, des algorithmes, et elle sert de base à la logique propositionnelle.
Dans l’algèbre de Boole, les opérations fondamentales sont l’ET logique, le OU logique, et la négation logique (NOT). Ces opérations s’appliquent à des paires de variables booléennes et produisent un résultat booléen.
Un Exemple dans un Exemple
Maintenant, pour mieux comprendre ces opérations, prenons l’exemple d’une pièce avec un interrupteur A et un capteur B détectant la présence de personnes contrôlant la lumière.
Interrupteur A ET Capteur B (A ET B) :
• Si l’interrupteur A est activé (A = 1) ET que le capteur B détecte des personnes (B = 1), alors la condition C « la lumière s’allume » est VRAIE (C = 1).
• Si l’interrupteur A est désactivé (A = 0), même si le capteur B détecte des personnes (B = 1), la condition C est FAUSSE ( C = 0).
• Si l’interrupteur A est activé (A = 1) mais le capteur B ne détecte pas de personnes (B = 0), la condition C est également FAUSSE (C=0).
• Si les deux, l’interrupteur A et le capteur B , sont désactivés (A=0 et B=0), la condition C est FAUSSE (C=0).
Interrupteur A OU Capteur B (A OU B) :
• Si l’interrupteur A est activé (A = 1) OU que le capteur B détecte des personnes (B = 1) alors la condition C est VRAIE (C=1)
• Si l’interrupteur A est désactivé (A = 0) OU le capteur B détecte des personnes (B = 1) alors la condition C est VRAIE (C=1).
• Si les deux, Si l’interrupteur A est activé (A = 1) ou le capteur B ne détecte pas de personne (B = 0) alors la condition est VRAIE (C=1).
• Si l’interrupteur A est désactivé (A = 0) ou le capteur B ne détecte pas de personne (B=0) alors la condition C est FAUSSE (C = 0).
Dans ces exemples, l’opération ET nécessite que l’interrupteur soit activé et que des personnes soient détectées pour que la condition soit vraie. À l’inverse, l’opération OU requiert que l’interrupteur soit activé soit la présence de personnes soit détectée pour que la condition soit vraie.
On peut tout résumer dans ces deux tableaux :
| A | B | A AND B |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
| A | B | A OR B |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
Ces opérations de base peuvent être combinées pour former des expressions logiques plus complexes, permettant de représenter des conditions (pas seulement deux comme dans l’exemple précédent) et des raisonnements logiques.
L’algèbre de Boole trouve des applications pratiques dans la conception de circuits logiques, les systèmes de contrôle, l’informatique, et d’autres domaines où la logique binaire est utilisée pour modéliser des états et des décisions.
Revenons au Neurone
Scientifique du fond en levant la main pour demander la parole: « Mais qu’est ce qu’un neurone a à voir avec l’algèbre de Boole ? «
Le Dr. Ford rentre en détail dans les explications: « Faisons simple et considérons un neurone formel acceptant simplement deux variables d’entrée \(x_1\) et \(x_2\) que l’on place dans un vecteur d’entrée (c’est l’information que reçoit le neurone)
\begin{equation*} \mathbf{X}=\left[ \begin{array}{c} x_{1} \\ x_{2} \end{array} \right]. \end{equation*}
Sachant que les entrées peuvent seulement valoir 0 ou 1 dans notre cas on a seulement 4 vecteurs entrée possibles
\begin{equation*} \left[ \begin{array}{c} 0 \\ 0 \end{array} \right]\quad \left[ \begin{array}{c} 0 \\ 1 \end{array} \right]\quad \left[ \begin{array}{c} 1 \\ 0 \end{array} \right]\quad \left[ \begin{array}{c} 1 \\ 1 \end{array} \right] \end{equation*}
On lui définit aussi les deux paramètres synaptiques \(w_1\) et \(w_2\) que l’on place aussi dans un vecteur que l’on note W.
\begin{equation*} \mathbf{W}=\left[ \begin{array}{c} w_{1} \\ w_{2} \end{array} \right]. \end{equation*}
Ceux-ci peuvent valoir soit 1 soit -1 donc comme précédemment on à seulement 4 vecteurs poids possible
\begin{equation*} \left[ \begin{array}{c} -1 \\ -1 \end{array} \right]\quad \left[ \begin{array}{c} -1 \\ 1 \end{array} \right]\quad \left[ \begin{array}{c} 1 \\ -1 \end{array} \right]\quad \left[ \begin{array}{c} 1 \\ 1 \end{array} \right] \end{equation*}

Maintenant on peut entamer la phase d’agrégation qui prend d’abord une entrée, lui associe un poids correspondant, somme et ajoute un biais noté b. En voici le résultat:
\[ \Sigma = w_1 x_1 + w_2 x_2 +b \]
on place le tout dans un tableau
Ensuite on passe à la phase d’activation c’est à dire qu’on introduit la valeur obtenu \(\Sigma\) dans notre fonction seuil que nous noterons H et qui détermine la sortie du neurone comme suit
\[ y = H(\Sigma+b)\]
En appliquant un raisonnement similaire, on observe qu’un neurone à une seule entrée peut soit ne produire aucun effet (neurone identité) soit effectuer une opération de NON logique.
En établissant un lien avec l’algèbre de Boole, nous avons démontré comment ce modèle pouvait réaliser des opérations logiques fondamentales, telles que le OU et le ET.
Cependant, en dépit de ses avancées, ce modèle seul présente deux limitations majeures : premièrement, il est limité à des opérations simples, et deuxièmement, il ne dispose d’aucun mécanisme d’apprentissage. Comme illustré précédemment, les seules opérations que nous pouvons effectuer sont le OU et le ET et nous devons manuellement déterminer les valeurs des poids pour effectuer ces opérations logiques spécifiques. Ces limitations ont motivé le développement ultérieur de modèles plus sophistiqués dans le domaine du Deep Learning, notamment en mettant en réseau ces modèles de neurones, nous avons la capacité de résoudre pratiquement n’importe quel problème de logique booléenne. Si de plus, nous autorisons le modèle à apprendre de manière autonome, il devient alors possible d’aborder des problématiques plus complexes et d’élargir considérablement ses capacités.
L'avènement du Perceptron
Le perceptron, conçu par le psychologue américain Frank Rosenblatt une quinzaine d’années après l’introduction du concept de neurone formel par McCulloch et Pitt, marque une avancée significative avec l’introduction du premier algorithme d’apprentissage du Deep Learning.
Le modèle du perceptron partage une similitude frappante avec celui que nous venons d’étudier. En fait, la seule différence entre le perceptron et le neurone formel précédent réside dans l’ajout d’un algorithme d’apprentissage qui lui permet de déterminer les valeurs de ses paramètres W, afin d’obtenir les sorties y souhaitées, éliminant ainsi la nécessité d’une recherche manuelle par les humains.
F. Rosenblatt s’est inspiré de la loi de Hebb en neuroscience, suggérant que le renforcement des liens synaptiques entre deux neurones biologiques se produit lorsqu’ils sont excités conjointement, un phénomène connu sous le principe « cells that fire together, wire together. » Cette plasticité synaptique est cruciale dans la construction de la mémoire et l’apprentissage.
La Loi de Hebb
L’algorithme d’apprentissage du perceptron consiste donc à entraîner le neurone artificiel sur des données de référence (X, y). À chaque activation de l’entrée X en même temps que la sortie y présente dans les données, les paramètres W sont renforcés. F. Rosenblatt a formulé cette idée avec l’équation suivante :
\[W^* = W + \delta(y_{\text{ref}} – y)X\]
où les nouveaux poids \(W^*\) sont mis à jour grâce à un taux d’apprentissage \(\delta\). \(y_{\text{ref}}\) est la sortie de référence, y est la sortie produite par le neurone, et X est l’entrée du neurone.
Cette formule permet d’ajuster les poids de manière à minimiser la différence entre la sortie attendue et la sortie produite par le neurone. Ainsi, si le neurone produit une sortie différente de celle attendue (par exemple, y=0 au lieu de y=1), les poids associés aux entrées activées sont augmentés. Ce processus continue jusqu’à ce que la sortie du neurone converge vers la sortie attendue.
Limites du Modèle
Mesdames et messieurs de la communauté scientifique, considérons le dorénavant un perceptron composé d’uniquement de deux entrées \(x_1\) et \(x_2\). Sa fonction d’agrégation est donc \(f(x_1, x_2) = w_1x_1 + w_2x_2\) et, par sa forme, peut modéliser des relations linéaires. Cependant, cette simplicité comporte des limitations lorsque nous somme confronté à des problèmes non linéaires.
Le Dr. Ford souligne avec sagacité : « Le perceptron, dans son essence, est comme un outil avec une perspective restreinte. Il peut réussir à effectuer des prédictions sommaires, mais il peine à saisir la complexité des relations non linéaires présentes dans le monde réel. »
Un scientifique de l’audience, affichant une compréhension profonde : « C’est comme si nous essayions de prédire le comportement d’un cercle en traçant qu’une ligne à la règle. »
Dr. Ford, souriant : « Exactement ! C’est pourquoi nous explorons des approches plus complexes pour modéliser la richesse des relations. »
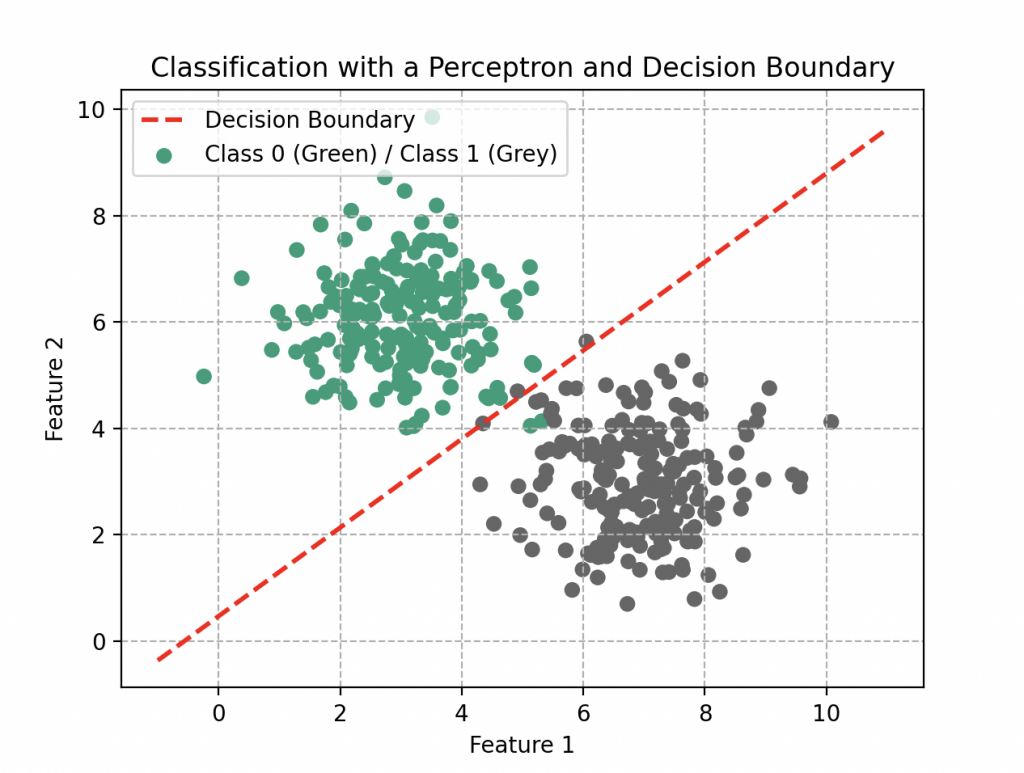
Quelques Perceptrons en plus
Pour surmonter ce premier problème, introduisons tout d’abord trois perceptrons que nous relierons ensemble. Les deux premiers recevront chacun les entrées \(x_1\) et \(x_2\), effectueront leurs calculs en fonction de leurs paramètres, puis renverront une sortie y vers le troisième perceptron. Ce dernier effectuera également ses propres calculs pour produire une sortie finale.

Essayez de programmer trois neurones de cet hôte et vous pourrez tracer la représentation graphique de la sortie finale en fonction des entrées \(x_1\) et \(x_2\), vous obtiendrez alors un modèle non linéaire, bien plus intéressant.
Ce modèle sera alors votre premier réseau de neurones artificiels, composé de 3 neurones répartis en deux couches : une couche d’entrée et une couche de sortie. Vous pouvez ajouter autant de couches et de neurones que vous le souhaitez, mais plus vous en ajouterez, plus la simulation de résultats complexes demandera de temps de calcul et de ressource. Vous pouvez aussi changer la topologie, c’est à dire la nature des connexions entre les neurones. Cela dépendra du problème à traiter. C’est ce que nous allons voir maintenant.
Les Réseaux de Neurones
Les réseaux de neurones, aussi appelés réseaux neuronaux artificiels, sont des modèles computationnels inspirés de la structure et du fonctionnement du cerveau humain. Ils se composent de neurones artificiels interconnectés et organisés en couches. Chaque neurone reçoit des entrées, effectue des opérations de traitement, puis transmet une sortie. Ces sorties sont ensuite transmises aux neurones de la couche suivante, créant ainsi une architecture en couches.
Les réseaux de neurones comprennent trois types de couches principales :
1. Couche d’entrée (Input Layer) : Recevant les données d’entrée du système, chaque nœud de cette couche représente une caractéristique ou une variable d’entrée.
2. Couches cachées (Hidden Layers) : Ces couches effectuent des opérations de transformation des données. Chaque nœud dans une couche cachée prend des entrées, applique des poids et des biais, puis produit une sortie. Elles sont cruciales pour que le réseau apprenne des représentations complexes des données.
3. Couche de sortie (Output Layer) : Produisant la prédiction ou la classification finale, cette couche synthétise les informations apprises par les couches cachées pour générer la sortie finale.
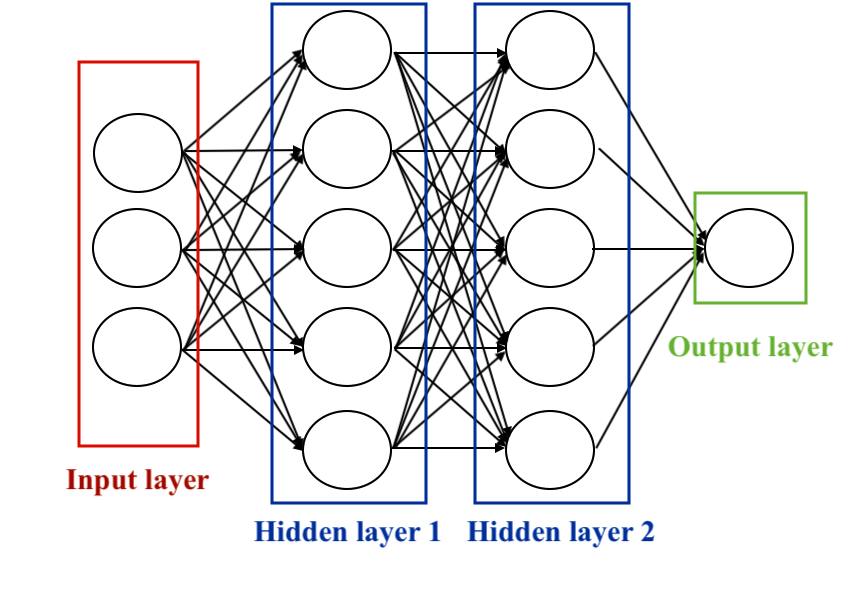
Il existe plusieurs types de réseaux de neurones selon la topologie des connexions entre les neurones. La topologie peut varier en fonction de l’architecture spécifique du réseau, mais certaines régularités sont couramment observées. Voici quelques exemples de topologies :
• Le perceptron multicouche (Multi-layer perceptron) : Chaque neurone de la couche est connecté à tous les neurones de la couche suivante. C’est une configuration simple utilisée notamment pour la classification d’images.
• Réseau Convolutif (Convolutional Neural Network – CNN) : Spécialisé dans le traitement d’images, il utilise des filtres pour analyser des parties locales, réduisant ainsi le nombre de paramètres et extrayant des caractéristiques importantes.
• Réseau Récurrent (Recurrent Neural Network – RNN) : Conçu pour traiter des données séquentielles, il utilise des connexions récurrentes pour prendre en compte la séquence temporelle des données.
• Réseau à Mémoire Longue (Long Short-Term Memory – LSTM) : Une extension des RNN, les LSTM traitent des séquences plus longues en évitant la disparition du gradient.
• Réseau Autoencodeur : Destiné à l’apprentissage non supervisé, le réseau autoencodeur est constitué d’une couche d’encodeur et d’une couche de décodeur. Son objectif est de reproduire l’entrée tout en générant une représentation latente. L’accent est mis sur la réduction de dimension, particulièrement utile lorsqu’il y a un volume important de données. En substituant ces données par une représentation dans un espace de dimension inférieure, on optimise le traitement par les processeurs, améliorant ainsi l’efficacité du modèle (on en parlera dans un autre article).
• Réseau de Neurones Résiduel (Residual Neural Network – ResNet) : Introduit pour résoudre le problème de la disparition du gradient, les ResNets utilisent des connexions résiduelles pour faciliter l’apprentissage de représentations plus profondes.
Dans cette exploration, nous nous concentrerons particulièrement sur les réseaux de neurones à propagation avant. C’est le premier type de réseau neuronal artificiel, le plus simple, où l’information se déplace uniquement vers l’avant, des nœuds d’entrée aux nœuds de sortie, sans cycles ou boucles (on dit qu’il est acyclique, se distinguant ainsi des réseaux récurrents). Le perceptron seul que nous avons déjà vu, puis son extension la plus connue, le perceptron multicouche que nous allons voir tout de suite.
Mais au fait, j’avais oublié, comment entraîner un réseau de neurones pour qu’il réalise ce qu’on lui demande, c’est-à-dire comment trouver les paramètres w et b de manière à obtenir le bon modèle ?
L’ensemble de l’auditoire reste muet.
Ne vous en faites pas c’est maintenant qu’on voit ça.
Programmation Cognitive des Hôtes à Reconnaissance de Chiffres Manuscrits: Le Perceptron Multicouche
Avant que nos hôtes ne puissent exceller dans des tâches plus avancées, telles que la reconnaissance d’êtres humains ou même d’émotions, il est impératif de les initier aux fondamentaux, à commencer par la reconnaissance de chiffres manuscrits car comme le dit le proverbe, « Avant d’apprendre à courir, il faut apprendre à marcher ».
Pour les guider dans cet apprentissage (supervisé), nous utilisons une série d’images de chiffres, chacune représentant visuellement la correspondance entre la forme manuscrite et le chiffre en question.
Ensuite, nos hôtes sont mis au défi de reconnaître les chiffres qui leur sont présentés.

Ce modèle de classification constitue le premier réseau de neurones artificiels de nos hôtes avec une couche d’entrée, plusieurs couches cachées que l’on déterminera et une couche de sortie. Un tel réseau multicouche, où la complexité peut être augmentée en ajoutant plus de couches et de neurones, mais cela nécessitera plus de temps de calcul.
Maintenant, explorons le processus auquel nos hôtes sont soumis lors de leur programmation pour maîtriser cette tâche.
Assimilation des Données d'Entraînement (DataSet)
Nos hôtes sont alimentés en données d’entraînement, composées de 60 000 exemples d’images en niveau de gris de chiffres manuscrits de résolution 28 pixel par 28 pixel et de leurs correspondances respectives. Ces données sont cruciales pour enseigner aux hôtes à généraliser à partir d’exemples existants. Et 10 000 images de test de même format pour les examiner, c’est à dire savoir s’ils ont bien réussi à classer les images. Voici les chiffres de 0 à 9:




De telles images sont simplement des tableaux de données contenant des chiffres de 0 à 255. Chacun des 60 000 tableaux est « aplati » pour former 60 000 vecteur X avec 784 coordonnées correspondant aux nombre total de pixel dans une image avec une étiquette y entre 0 et 9.
Construction du Modèle Cognitif
Le modèle cognitif représente la structure du réseau de neurones dans l’esprit de nos hôtes, englobant des aspects tels que le nombre de couches, le nombre de neurones par couche, les paramètres d’apprentissage (W et b), et même les fonctions d’activations. La conception du modèle dépend étroitement de la nature spécifique de la tâche à accomplir.
Les poids et biais subiront des ajustements continus tout au long de l’entraînement afin de minimiser l’erreur entre les prédictions du modèle et les sorties attendues. L’initialisation et la mise à jour appropriées de ces paramètres sont cruciales pour optimiser la performance du réseau. Les autres paramètres comme le nombre de couches, le nombre de neurones seront ajustés manuellement afin de trouver le modèle le plus efficace dans un délai raisonnable et sans consommer excessivement de ressources car il est peu souhaitable qu’un hôte mette 30 secondes à reconnaître un chiffre manuscrit ou qu’il soit inactif pendant cette tâche.
Propagation vers l'Avant
La première étape de ce processus cognitif est la propagation vers l’avant (forward propagation) : le cerveau des hôtes fait circuler les informations des pixels de la première couche jusqu’à la dernière pour produire une sortie y (l’étiquette du chiffre manuscrit).
Analysons son fonctionnement.
• La couche d’entrée est constituée de seulement 784 neurones, chacun analysant un pixel de l’image. Elle ne compte aucun paramètre.
• Les couches cachées (sigmoïde) : ensuite, nous dotons nos hôtes de deux couches cachées, comprenant chacune 100 neurones avec une fonction d’activation de type sigmoïde.
La sortie de la première couche nous fourni un vecteur \(A^1\) contenant 100 coordonnées (une pour chaque neurones). Les calculs effectués pour chaque éléments sont simples et sont calqués sur le modèle du perceptron: on calcule la fonction d’agrégation puis on lui applique la fonction d’activation.

On écrit tout d’une manière compacte sous forme matricielle.
\begin{align*}
Z^{1} &= W^{1}\cdot X+b^1\\
A^{1} &= \frac{1}{1+\exp{(-Z^{1})}}
\end{align*}
La deuxième couche cachée fourni un vecteur \(A^2\) contenant aussi 100 coordonnées. On fait pareil pour la deuxième couche
\begin{align*}
Z^{2} &= W^{2}\cdot A^{1}+b^2\\
A^{2} &= \frac{1}{1+\exp{(-Z^{2})}}
\end{align*}
• La couche de sortie: Enfin, comme l’objectif est de classifier les chiffres de 0 à 9, une couche de sortie composée de 10 neurones, accompagnée d’une fonction d’activation de type softmax, est amplement suffisante.
\begin{align*}
Z^{3} &= W^{3}\cdot A^{2}+b^2\\
A^{2} &= \frac{1}{1+\exp{(-Z^{3})}}
\end{align*}
La fonction softmax assigne des probabilités à chaque classe possible. Pour chaque image en entrée, elle attribue une probabilité d’appartenir à la classe 0, 1, 2, …, jusqu’à 9. Voici un exemple

| Chiffres | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|---|---|
| Probabilités | 0.00000028 | 0.00000000023 | 0.000017 | 0.000070 | 0.00000000019 | 0.00000030 | 0.000000000018 | 0.99 | 0.0000018 | 0.000022 |
D’après ce tableau il n’y a quasiment aucun doute, ce chiffre est à 99% un 7, l’hôte lui assignera donc ce chiffre. De manière générale l’hôte assignera à l’image l’étiquette qui a la plus grande probabilité.
Cette fonction permet donc d’interpréter les résultats comme la confiance du modèle dans chaque classe, et facilite la prise de décision dans le contexte d’une tâche de classification multiclasse.
Analyse de l'Erreur Cognitive: La Fonction Coût
Dans la deuxième phase, le réseau neuronal de l’hôte procède à l’analyse de l’erreur entre la sortie y (sa prédiction) du modèle et la sortie de référence attendue (\(y_{\text{ref}}\)). Cette évaluation s’effectue en utilisant une fonction de coût fréquemment utilisé dans les tâches de classification, y compris la reconnaissance de chiffres manuscrits, en l’occurrence, il s’agit de la cross-entropie catégorique, que nous avons déjà rencontrée précédemment (sous une autre forme).

On rappelle son expression:
\begin{align*}L(W,b)=-\frac{1}{n}\sum_{k=1}^n\left[y^{(k)}\log{y_{\text{ref}}}+\left(1-y^{(k)}\right)\log{\left(1-y_{\text{ref}}\right)}\right].\end{align*}
De manière générale, \(y_{ref}\) peut être la sortie finale mais aussi n’importe quelle sortie de couche de neurone \(A^{i}\) avec i la i-ème couche que l’on place dans un tableau nommé \(\mathbf{A}\). Ce qui donne la formule matricielle suivante:
\begin{align*}L(W,b)=-\frac{1}{n}\left[\mathbf{y}\log{\mathbf{A}}+\left(1-\mathbf{y}\right)\log{\left(1-\mathbf{A}\right)}\right].\end{align*}
C’est un élément crucial de l’analyse cognitive du modèle et elle mesure la différence entre les probabilités prédites par le modèle et les probabilités réelles des classes. Son objectif est de quantifier de manière appropriée l’écart entre les prédictions du réseau neuronal et les véritables labels associés aux images de chiffres. Une minimisation efficace de cette fonction coût lors de l’entraînement contribue à affiner les paramètres du modèle pour une meilleure performance.
Mécanismes de Compréhension
La troisième étape est rétropropagation. Les hôtes mesurent comment cette fonction coût varie par rapport à chaque couche du modèle, en remontant de la dernière à la première. C’est à dire qu’ils vont analyser l’erreur de la sortie et de l’avant dernière couche, puis de l’avant dernière couche et l’avant avant dernière couche etc jusqu’à remonter à la couche d’entrée.
En somme, il faut calculer comment l’erreur se propage de la sortie vers l’entrée pour pouvoir la réduire. Sur ce réseau avec deux couches cachées cela donne 6 expressions terrifiantes (si vous retenez juste la phrase précédente c’est nickel):
On commence par la dernière (de la sortie à la deuxième)
\begin{align*}
\frac{\partial L(\mathbf{W},b)}{\partial \mathbf{W}^3} =\frac{\partial L}{\partial \mathbf{A}^3} \times \frac{\partial \mathbf{A}^3}{\partial \mathbf{Z}^3} \times \frac{\partial \mathbf{Z}^3}{\partial \mathbf{W}^3}
\end{align*}
\begin{align*}
\frac{\partial L(\mathbf{W},b)}{\partial \mathbf{b}^3} =\frac{\partial L}{\partial \mathbf{A}^3} \times \frac{\partial \mathbf{A}^3}{\partial \mathbf{Z}^3} \times \frac{\partial \mathbf{Z}^3}{\partial \mathbf{b}^3}
\end{align*}
l’avant dernière (de la deuxième à la première)
\begin{align*}\frac{\partial L(\mathbf{W},b)}{\partial \mathbf{W}^2} =\frac{\partial L}{\partial \mathbf{A}^3} \times \frac{\partial \mathbf{A}^3}{\partial \mathbf{Z}^3} \times \frac{\partial \mathbf{Z}^3}{\partial \mathbf{A}^2}\times\frac{\partial \mathbf{A}^2}{\partial \mathbf{Z}^2} \times \frac{\partial \mathbf{Z}^2}{\partial \mathbf{W}^2}\end{align*}
\begin{align*}\frac{\partial L(\mathbf{W},b)}{\partial \mathbf{W}^2} =\frac{\partial L}{\partial \mathbf{A}^3} \times \frac{\partial \mathbf{A}^3}{\partial \mathbf{Z}^3} \times \frac{\partial \mathbf{Z}^3}{\partial \mathbf{A}^2}\times\frac{\partial \mathbf{A}^2}{\partial \mathbf{Z}^2} \times \frac{\partial \mathbf{Z}^2}{\partial \mathbf{}^2}\end{align*}
et enfin l’entrée (de la première à l’entrée)
\begin{align*}\frac{\partial L(\mathbf{W},b)}{\partial \mathbf{W}^1} =\frac{\partial L}{\partial \mathbf{A}^3} \times \frac{\partial \mathbf{A}^3}{\partial \mathbf{Z}^3} \times \frac{\partial \mathbf{Z}^3}{\partial \mathbf{A}^2}\times\frac{\partial \mathbf{A}^2}{\partial \mathbf{Z}^2}\times \frac{\partial \mathbf{Z}^2}{\partial \mathbf{A}^1}\times\frac{\partial \mathbf{A}^1}{\partial \mathbf{Z}^1} \times \frac{\partial \mathbf{Z}^1}{\partial \mathbf{W}^1} \end{align*}
\begin{align*}\frac{\partial L(\mathbf{W},b)}{\partial \mathbf{b}^1} =\frac{\partial L}{\partial \mathbf{A}^3} \times \frac{\partial \mathbf{A}^3}{\partial \mathbf{Z}^3} \times \frac{\partial \mathbf{Z}^3}{\partial \mathbf{A}^2}\times\frac{\partial \mathbf{A}^2}{\partial \mathbf{Z}^2}\times \frac{\partial \mathbf{Z}^2}{\partial \mathbf{A}^1}\times\frac{\partial \mathbf{A}^1}{\partial \mathbf{Z}^1} \times \frac{\partial \mathbf{Z}^1}{\partial \mathbf{b}^1} \end{align*}

Optimisation Mentale
Pour terminer, la quatrième étape est l’optimisation mentale. Les hôtes ajustent mentalement chaque paramètre du modèle grâce à de la descente de gradient (vous vous souvenez ? voir l’article ), avant de revenir à la première étape, la propagation avant, pour recommencer un cycle d’entraînement.
\begin{align*}\mathbf{W^*}=\mathbf{W}-\delta \frac{\partial }{\partial \mathbf{b}}L(\mathbf{W},\mathbf{b})\\
\mathbf{W^*}=\mathbf{W}-\delta \frac{\partial }{\partial \mathbf{W}}L(\mathbf{W},\mathbf{b})
\end{align*}
avec \(\delta\) le taux d’apprentissage de l’ensemble des neurones.
En résumé, ce processus permet à nos hôtes de maîtriser, dans une certaine mesure, la reconnaissance de chiffres manuscrits avec un taux de réussite d’environ 83%, bien que cette performance ne soit pas exceptionnelle. Voici quelques erreurs que commettent les hôtes:
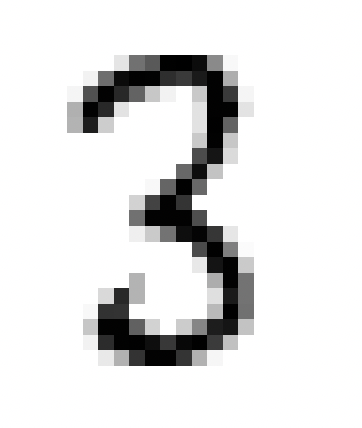
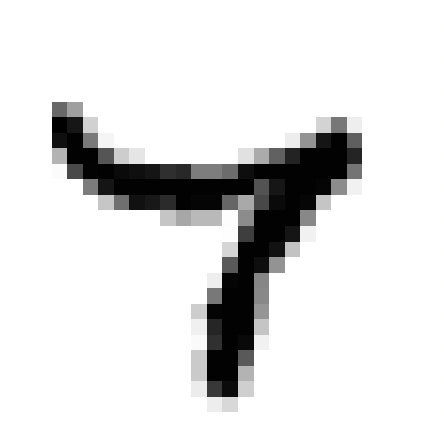


Clairement certains chiffres manuscrits peuvent prêter à confusion, même pour l’œil humain, tandis que d’autres semblent être sans aucun doute identifiables, comme le 3 ci-dessus.

Ainsi, en ajustant quelques paramètres, il devient relativement facile d’améliorer significativement les performances du modèle et d’atteindre les 94% de précision, une compétence cruciale dans leur parcours vers l’acquisition de tâches cognitives plus avancées.
À mesure que nos hôtes progressent, ils élargiront leur champ d’expertise, débloquant de nouvelles possibilités pour des expériences plus immersives à Westworld.
Les Hôtes de Westworld : Des Chiffres aux Visages
En conclusion, mes chers invités, notre première exploration dans les arcanes du Deep Learning se termine ici. Je suis très heureux de vous avoir révélé de nombreux concepts parmi lesquels les neurones formels, des perceptrons et des perceptrons multicouches. Nous avons analysé un exemple concret où les hôtes de Westworld, au travers de leur processeur, ont acquis la capacité à reconnaître et à interpréter des chiffres manuscrits avec une précision déconcertante.
Cependant ne vous y méprenez pas, ce réseau neuronal seul est bien loin de suffire lorsque le monde à analyser possède une plus grande résolution. Le nombre de paramètres d’apprentissage qui ont du être ajustés pour notre perceptron multicouche (il y avait en beaucoup! 89 610 paramètres) de seulement deux couches cachées de 100 neurones était relativement faible pour pouvoir être lancé sur des machines peu puissantes. Imaginez maintenant, simuler de tel modèle avec des centaines de couches et des milliers de neurones par couche. Cela serait impossible ! C’est la raison pour laquelle d’autres techniques ont été développé comment les réseaux de neurones convolutifs qui permettent d’analyser grâce à des filtres, des éléments caractéristiques de l’image.
Pour finir, et j’en resterez là, ne visualisez pas une intelligence artificielle discernant visages, des objets complexes ou des émotions comme « intelligent ». Car même si les hôtes semblent approcher de manière saisissante l’humanité dans leurs interactions, rappelons-nous toujours qu’ils ne sont rien de plus que des machines.
Dr. Ford - "N'oubliez pas, les hôtes ne sont pas réel. Ils ne sont pas conscients"

Bibliographie
F. Rosenblatt, The Perceptron, A perceiving and recognizing automaton, Cornell Aeronautical Laboratory, 1957
F. Rosenblatt, The Perceptron: A Probabilistic Model For Information Storage And Organization in the Brain, Psychological Review, vol. 65, no 6, 1958
M. Tommasi, Le Perceptron, Apprentissage automatique : les réseaux de neurones, cours à l’université de Lille 3.
D.B. Parker, Learning Logic , Massachusetts Institute of Technology, Cambridge MA, 1985.
G. Saint-Cirgue, Machine Learnia, Youtube Channel.
USI Events, Deep learning, Yann LeCun on Youtube.
Note: pour plus d'information sur les codes fournis rendez vous sur GitHub. Lien dans le pied de page !
import numpy as np
import matplotlib.pyplot as plt
# Set the random seed for reproducibility
np.random.seed(42)
# Generate points for class 0
class0_points = np.random.normal(loc=[3, 6], scale=[1, 1], size=(200, 2))
# Generate points for class 1
class1_points = np.random.normal(loc=[7, 3], scale=[1, 1], size=(200, 2))
M0 = np.zeros((class0_points.shape[0], 1))
M1 = np.ones((class1_points.shape[0], 1))
X = np.concatenate([class0_points, class1_points], axis=0)
y = np.concatenate([M0, M1], axis=0)
# Create an initialization function to initialize parameters W and b of our model
def initialization(X):
np.random.seed(seed=0)
W = np.random.randn(X.shape[1], 1)
b = np.random.randn(1)
return W, b
W, b = initialization(X)
print(W.shape)
# Next, create an iterative algorithm where we repeat the following functions in a loop:
# Start with the function that represents our artificial neuron model, where we find the function Z = X.W + b and the activation function A
def model(X, W, b):
Z = X.dot(W) + b
A = 1 / (1 + np.exp(-Z))
return A
A = model(X, W, b)
# Next, create an evaluation function, i.e., the cost function that evaluates the model's performance by comparing the output A to the reference data y
def log_loss(A, y):
return (1 / len(y)) * np.sum(-y * np.log(A) - (1 - y) * np.log(1 - A))
# In parallel, calculate the gradients of this cost function
def gradients(A, X, y):
dW = (1 / len(y)) * np.dot(X.T, A - y)
db = (1 / len(y)) * np.sum(A - y)
return dW, db
dW, db = gradients(A, X, y)
print(dW.shape)
print(db.shape)
# Finally, use these gradients in an update function that updates the parameters W and b to reduce the model's errors
def update(dW, db, W, b, learning_rate):
W = W - learning_rate * dW
b = b - learning_rate * db
return W, b
# Create a prediction function
def predict(X, W, b):
A = model(X, W, b)
return A >= 0.5
# Create an artificial neuron
def artificial_neuron(X, y, learning_rate=0.1, n_iter=100):
# Initialize W, b
W, b = initialization(X)
# Visualize the loss
Loss = []
# Create a training loop
for i in range(n_iter):
A = model(X, W, b)
Loss.append(log_loss(A, y))
dW, db = gradients(A, X, y)
W, b = update(dW, db, W, b, learning_rate)
# Calculate predictions for all data
y_pred = predict(X, W, b)
# Display the performance of our model (e.g., accuracy), comparing the reference data y with our predictions
# print(accuracy_score(y, y_pred))
# Visualize the loss to see if our model has learned well
plt.plot(Loss)
plt.grid(ls='--')
plt.show()
return W, b
# Train the artificial neuron
W, b = artificial_neuron(X, y)
# Test on new data
new_data = np.array([6, 4])
plt.scatter(X[:, 0], X[:, 1], c=y, cmap='Dark2', label='Class 0 (Blue) / Class 1 (Orange)')
plt.scatter(new_data[0], new_data[1], c='red', label='New Data (Red)')
plt.title('Classification with an Artificial Neuron')
plt.xlabel('Feature 1')
plt.ylabel('Feature 2')
plt.grid(ls='--')
plt.legend()
plt.show()
prediction = predict(new_data, W, b)
print(f"Prediction for new data: {prediction}")
# Create the decision boundary
x0 = np.linspace(-1, 11, 100)
x1 = (-W[0] * x0 - b) / W[1]
plt.plot(x0, x1, c='red', lw=2, ls='--', label='Decision Boundary')
plt.scatter(X[:, 0], X[:, 1], c=y, cmap='Dark2', label='Class 0 (Green) / Class 1 (Grey)')
plt.title('Classification with a Perceptron and Decision Boundary')
plt.xlabel('Feature 1')
plt.ylabel('Feature 2')
plt.grid(ls='--')
plt.legend()
plt.show()
import numpy as np
import matplotlib.pyplot as plt
from tqdm import tqdm
from sklearn.metrics import log_loss, accuracy_score
from keras.datasets import mnist
from sklearn.preprocessing import OneHotEncoder
# Load MNIST data
(X_train, y_train), (X_test, y_test) = mnist.load_data()
# Display one image for each digit
fig, ax = plt.subplots(nrows=1, ncols=10, figsize=(20, 4))
for digit in range(10):
digit_indices = np.where(y_train == digit)[0]
ax[digit].imshow(255 - X_train[digit_indices[0]], cmap='gray')
ax[digit].set_title(f'Digit {digit}')
ax[digit].axis('off')
plt.tight_layout()
plt.show()
# Reshape and normalize input data
X_train_reshape = X_train.reshape(X_train.shape[0], -1) / 255.0
X_test_reshape = X_test.reshape(X_test.shape[0], -1) / 255.0
# Transpose labels if needed
y_train = y_train.reshape(-1, 1)
y_test = y_test.reshape(-1, 1)
# One-hot encode labels
encoder = OneHotEncoder(sparse=False, categories='auto')
y_train_onehot = encoder.fit_transform(y_train)
y_test_onehot = encoder.transform(y_test)
# Select a subset of data
m_train = 5000
m_test = 1000
X_train_reshape = X_train_reshape[:m_train, :]
X_test_reshape = X_test_reshape[:m_test, :]
y_train_onehot = y_train_onehot[:m_train, :]
y_test_onehot = y_test_onehot[:m_test, :]
print(X_train_reshape.shape)
print(X_test_reshape.shape)
print(y_train_onehot.shape)
print(y_test_onehot.shape)
# Neural network initialization function
def initialization(dimensions):
np.random.seed(seed=0)
parameters = {}
C = len(dimensions)
for c in range(1, C):
parameters['W' + str(c)] = np.random.randn(dimensions[c], dimensions[c-1])
parameters['b' + str(c)] = np.random.randn(dimensions[c], 1)
return parameters
# Neural network forward propagation function
def forward_propagation(X, parameters):
activations = {'A0': X}
C = len(parameters) // 2
for c in range(1, C + 1):
Z = parameters['W' + str(c)].dot(activations['A' + str(c-1)]) + parameters['b' + str(c)]
activations['A' + str(c)] = 1 / (1 + np.exp(-Z))
return activations
# Neural network backpropagation function
def back_propagation(X, y, activations, parameters):
m = y.shape[1]
C = len(parameters) // 2
dZ = activations['A' + str(C)] - y
gradients = {}
for c in reversed(range(1, C + 1)):
gradients['dW' + str(c)] = (1/m) * np.dot(dZ, activations['A' + str(c-1)].T)
gradients['db' + str(c)] = (1/m) * np.sum(dZ, axis=1, keepdims=True)
if c > 1:
dZ = np.dot(parameters['W' + str(c)].T, dZ) * activations['A' + str(c-1)] * (1 - activations['A' + str(c-1)])
return gradients
# Neural network update function
def update(gradients, parameters, learning_rate):
C = len(parameters) // 2
for c in range(1, C + 1):
parameters['W' + str(c)] = parameters['W' + str(c)] - learning_rate * gradients['dW' + str(c)]
parameters['b' + str(c)] = parameters['b' + str(c)] - learning_rate * gradients['db' + str(c)]
return parameters
# Neural network prediction function
def predict(X, parameters):
activations = forward_propagation(X, parameters)
C = len(parameters) // 2
Af = activations['A' + str(C)]
return (Af >= 0.5).astype(int)
# Neural network training function
def neural_network(X, y, hidden_layers=(100, 100), learning_rate=0.1, n_iter=1000):
np.random.seed(0)
dimensions = [X.shape[0]] + list(hidden_layers) + [y.shape[0]]
parameters = initialization(dimensions)
train_loss = []
train_acc = []
for i in tqdm(range(n_iter)):
activations = forward_propagation(X, parameters)
gradients = back_propagation(X, y, activations, parameters)
parameters = update(gradients, parameters, learning_rate)
if i % 10 == 0:
C = len(parameters) // 2
train_loss.append(log_loss(y, activations['A' + str(C)]))
y_pred = predict(X, parameters)
current_accuracy = accuracy_score(y.flatten(), y_pred.flatten())
train_acc.append(current_accuracy)
plt.figure(figsize=(12, 4))
plt.subplot(1, 2, 1)
plt.plot(train_loss, label='train loss')
plt.legend()
plt.subplot(1, 2, 2)
plt.plot(train_acc, label='train acc')
plt.legend()
plt.show()
return parameters
# Train the neural network
parameters = neural_network(X_train_reshape.T, y_train_onehot.T, hidden_layers=(100, 100), learning_rate=0.1, n_iter=5000)
# Predict on test data
y_pred = predict(X_test_reshape.T, parameters)
# Print accuracy on test data
test_accuracy = accuracy_score(y_test_onehot.flatten(), y_pred.flatten())
print(f"Test Accuracy: {test_accuracy}")
import numpy as np
import tensorflow as tf
import keras
import matplotlib.pyplot as plt
from keras.datasets import mnist
# Load MNIST data
(X_train, y_train), (X_test, y_test) = mnist.load_data()
# Display one image for each digit
fig, ax = plt.subplots(nrows=1, ncols=10, figsize=(20, 4))
for digit in range(10):
digit_indices = np.where(y_train == digit)[0]
ax[digit].imshow(255 - X_train[digit_indices[0]], cmap='gray')
ax[digit].set_title(f'Digit {digit}')
ax[digit].axis('off')
plt.tight_layout()
#plt.show()
# Reshape and normalize input data
X_train = X_train/ 255.0
X_test = X_test / 255.0
hidden1 = 100
hidden2 = 100
model = keras.Sequential([
keras.layers.Input((28, 28)),
keras.layers.Flatten(),
keras.layers.Dense(hidden1, activation='relu'),
keras.layers.Dense(hidden2, activation='relu'),
keras.layers.Dense(10, activation='softmax')
])
model.compile(optimizer='adam',
loss='sparse_categorical_crossentropy',
metrics=['accuracy'])
batch_size = 512
epochs = 16
history = model.fit(X_train, y_train,
batch_size=batch_size,
epochs=epochs,
verbose=1,
validation_data=(X_test, y_test))
# Plot the training history
plt.plot(history.history['accuracy'], label='train accuracy')
plt.plot(history.history['val_accuracy'], label='validation accuracy')
plt.xlabel('Epochs')
plt.ylabel('Accuracy')
plt.legend()
#plt.show()
plt.plot(history.history['loss'], label='train loss')
plt.plot(history.history['val_loss'], label='validation loss')
plt.xlabel('Epochs')
plt.ylabel('Loss')
plt.legend()
#plt.show()
# Evaluate the model on the test set
score = model.evaluate(X_test, y_test, verbose=0)
print('Test Loss:', score[0])
print('Test Accuracy:', score[1])
# Predictions on the test set
y_pred = model.predict(X_test)
y_pred_classes = np.argmax(y_pred, axis=-1)
print(y_pred[0])
plt.figure(figsize=(20, 4))
plt.imshow(255 - X_test[0], cmap='gray')
plt.title(f'Digit: {y_test[0]}')
plt.axis('off')
plt.show()
print(model.summary())



