Wall-E: Le Compacteur Terrien de Déchets
Episode III
Par Jordan Moles le 2 Décembre, 2023

En tant que robot fidèle à sa mission et entre quelques estimations d’or, Wall-E n’oublie pas sa principale tâche : trier les déchets. C’est lors de ses expéditions dans les endroits reculés de la planète qu’il découvrit le défi ultime qui stimule son esprit curieux. Parmi les objets qu’il amasse, Wall-E tombe sur une collection variée de vieux composants électroniques, certains en bon état qu’il ramène à la base, et d’autres défectueux qu’il entrepose dans un coin.
Passionné par de tels objets, il se met à dévisser, à arracher et à classer soigneusement chaque composant en deux catégories distinctes (classification binaire): d’un côté les pièces de métal précieuses qu’il triera plus tard (Classification multiclasse) et de l’autre le plastique sans valeur. La question fondamentale est: comment réalise t’il une telle mission ?
Il est fortement conseillé d'avoir lu l'épisode I et II avant de continuer !
Les Nouveaux Horizons de Wall-E : La Classification
L’épopée de notre intrépide robot solitaire, Wall-E, prend une nouvelle dimension fascinante lors de son exploration du vaste royaume de la classification. Après avoir brillamment maîtrisé l’art de la régression lors de l’épisode précédent (voir l’article Wall-E le petit mineur d’or), Wall-E entreprend courageusement une nouvelle phase en se lançant dans le tri binaire entre métaux précieux et plastiques. Cette première étape préparatoire marque le début d’une quête plus complexe, où Wall-E déploie avec audace ses compétences en classification pour naviguer parmi les métaux variés qui jalonnent son chemin.
S’appuyant sur ses succès initiaux, Wall-E décide d’élargir son champ d’action en s’attaquant à la classification multi-classe des métaux, faisant ainsi de l’algorithme K-Nearest Neighbors (KNN) son allié privilégié. Ce nouveau défi demande à Wall-E une compréhension plus approfondie, car il doit non seulement distinguer entre deux catégories, mais également classifier différents types de métaux tels que le bronze, l’or et l’argent.
Cette nouvelle phase de son aventure marque la métamorphose de Wall-E vers des horizons de classification plus vastes et sophistiqués. Chaque étape de cette exploration confère une nouvelle dimension à ses compétences, préparant ainsi Wall-E à affronter des défis plus complexes que le simple tri binaire. Dans cette démarche, la sélection du modèle se révèle cruciale pour assurer la précision de ses prédictions. Wall-E appréhende l’importance du processus de validation croisée et explore avec minutie les subtilités de l’ajustement des hyperparamètres, assurant ainsi la robustesse et l’efficacité de son modèle.
L'Élément Clé : Toujours Les Données
Dans son exploration pour décoder la nature des composants électroniques, Wall-E puise dans les informations emmagasinées lors de son apprentissage avec ses créateurs. Cette démarche vise à constituer un ensemble étendu et variés d’échantillons, s’inscrivant en parallèle à ses défis associés à la régression.
À la Rencontre des Échantillons
Chaque exemple k était un élément avec des caractéristiques spécifiques, telles que la densité \(x^{(k)}\), la conductivité thermique \(x_2^{(k)}\), électrique \(x_3^{(k)}\) etc. Pour illustrer notre cas simplement, nous allons considérer uniquement et seulement maintenant la variable densité \(x^{(k)}\).
Ainsi, pour chaque échantillon k, Wall-E note s’il est un métal (étiqueté comme \(y^{(k)}=1\)) ou un plastique (étiqueté comme \(y^{(k)}=0\)). Ces échantillons et leurs étiquettes forme ainsi son ensemble de données d’apprentissage. En voici un exemple concret de 5 échantillons (parmi les 650 qu’il connaît déjà).
| Densité | Type de Composant | |
|---|---|---|
| Echantillon 1 | 2.165747 | Plastique |
| Echantillon 2 | 7.151579 | Métal |
| Echantillon 3 | 0.901240 | Plastique |
| Echantillon 4 | 19.24357 | Métal |
| Echantillon 5 | 12.54564 | Métal |
Les Frontières de la Décision
La difference avec le problème précédent est qu’il faut définir ici ce que l’on nomme une frontière de décision. Expliquons ce concept simplement. Au lieu de regarder chaque objet individuellement, Wall-E décide de diviser cet espace en différentes régions. Chaque région serait destinée à recevoir un type spécifique d’objet, soit métal, soit plastique. Les limites de ces régions définiront des frontières, et c’est là que réside le cœur du problème de classification.
Lorsque Wall-E dessine ces frontières, il veut s’assurer que les objets similaires se trouvent dans la même région. Cela signifie que les objets proches en densité les uns des autres ont tendance à avoir la même étiquette, soit métal, soit plastique. Idéalement, il aimerait que ces deux groupes soient parfaitement séparés, comme s’ils étaient dans des boîtes distinctes. Une simple ligne pourrait faire l’affaire.
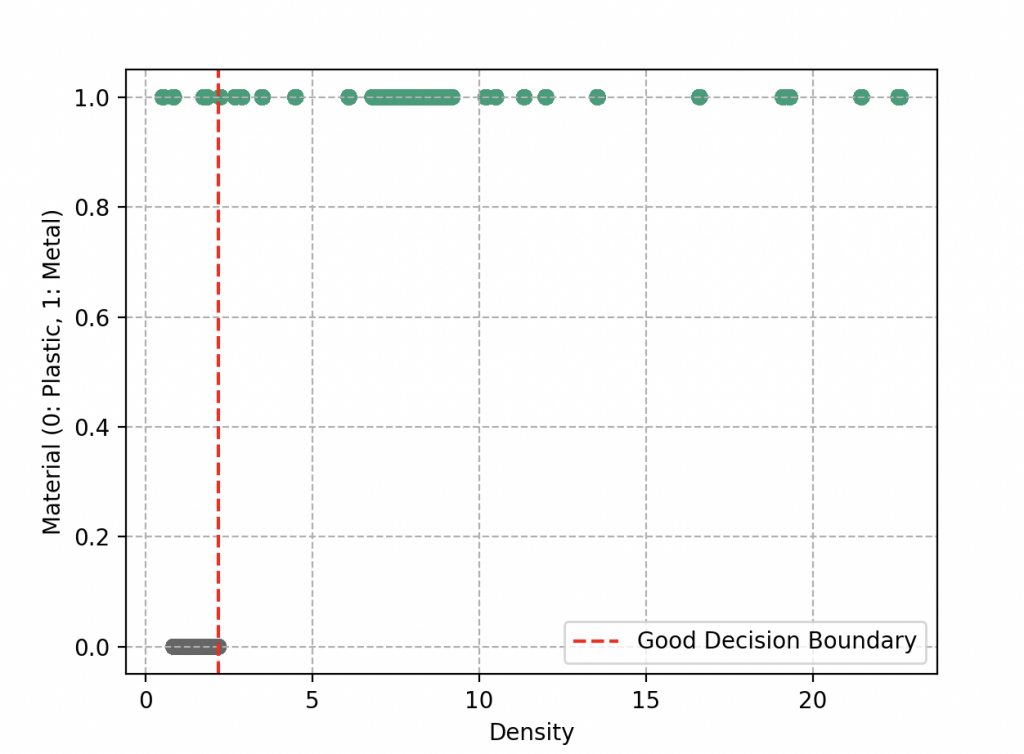

Cependant, la réalité n’est pas toujours aussi simple. Parfois, il y a des objets qui sont mal placés et se retrouvent de l’autre côté de la ligne. C’est ce qu’il se passe, lorsque dans notre exemple, certains plastiques ont une plus grande densité que certains métaux (comme par exemple le caoutchouc et le lithium qui se retrouvent à gauche de la frontière de décision). Cela pose un défi à Wall-E. Il doit maintenant juger son travail en fonction de la qualité de la séparation. Plus la séparation est nette, mieux c’est. Les objets mal classés sont comme des erreurs sur sa feuille de tri, et il souhaite comme d’habitude minimiser ces erreurs.
Wall-E est aussi conscient qu’il ne doit pas se compliquer la tâche en dessinant des frontières zigzagantes et complexes. Ces frontières compliquées pourraient capturer tous les objets, mais cela pourrait aussi le mener à un tri excessif, où chaque objet est dans sa propre région. Cela s’appelle le sur-apprentissage (on verra ça dans quelques sections).
Création du Modèle de Classification Binaire
Animé par le désir de donner un sens à ces composants électroniques, Wall-E s’engage dans la création d’un modèle de classification binaire. Ce modèle prendra les caractéristiques d’un composant en entrée et donnera en sortie une prédiction de sa nature. Après avoir exploré différentes approches, dont la régression linéaire comme il sait faire avec la fonction \(f(x)= ax+b\) (avec les paramètres a et b) qui ne s’ajuste absolument pas aux données,


Wall-E opte plutôt pour un modèle classique de Régression logistique dont la fonction associée (comprise entre 0 et 1) s’exprime de la manière suivante
\begin{align*}
\sigma(x)=\frac{1}{1+\exp{(-x)}}
\end{align*}
Elle se nomme fonction logistique ou sigmoïde (à cause de sa forme en « S », voir ci-contre).
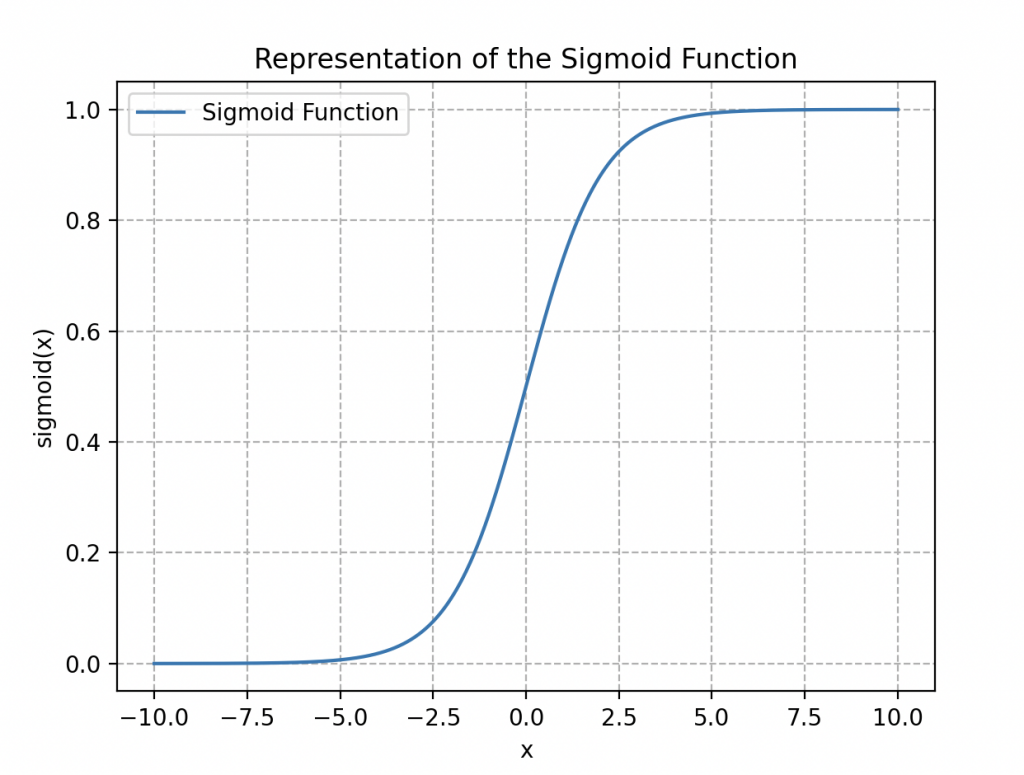
En appliquant cette fonction à notre dataset on obtient
\begin{align*}
\sigma(z)=\frac{1}{1+\exp{(-z)}}
\end{align*}
ou z peut être une fonction linéaire comme \(ax+b\) ou polynomiale comme par exemple \(ax^2 +bx+c\) (polynôme de degré 2) avec a, b et c les paramètres à ajuster.
Le gros avantage d’une telle fonction est que nous pouvons définir très facilement une frontière de décision en fixant ce que l’on appelle une valeur seuil de décision.


Pour comprendre formellement pourquoi nous introduisons une telle fonction, il faut bien comprendre que dans le monde de la classification, l’idée pour Wall-E est d’estimer la probabilité d’appartenance d’un échantillon à chaque catégorie (métal ou plastique), permettant ainsi de classer avec assurance chaque nouvelle observation dans la catégorie associée à la probabilité la plus élevée. Ainsi lorsqu’il est proche de la bonne réponse, la probabilité doit être très proche de 1 et inversement si sa réponse s’éloigne de la réalité alors la probabilité est presque nulle.
Le robot s’inspire donc de cette notion fondamentale lorsqu’il aborde le concept de la fonction sigmoïde. Il comprend que cette fonction peut être utilisée pour transformer les résultats de la Régression logistique en probabilités. Comme s’il appliquait une sorte de filtre mathématique à son évaluation, la fonction sigmoïde attribue à chaque composant une probabilité d’appartenir à une catégorie donnée. Ainsi si cette probabilité est supérieure à 0.5, on classifie l’objet dans la catégorie « métal » si elle est inférieure à 0.5 ça sera du plastique.
Évaluation des Prédictions : La Fonction de Coût
Wall-E a élaboré son modèle, mais il désire évaluer la précision de ses prédictions. Pour ce faire, il entreprend d’utiliser une des fonction coût de la régression, la MSE (voir article Wall-E le petit mineur d’or) définie comme suit:
\begin{align*}
MSE(a, b) =\frac{1}{n} \sum_{k=1}^{n} \left(\sigma(x^{(k)})- y^{(k)}\right)^2.
\end{align*}
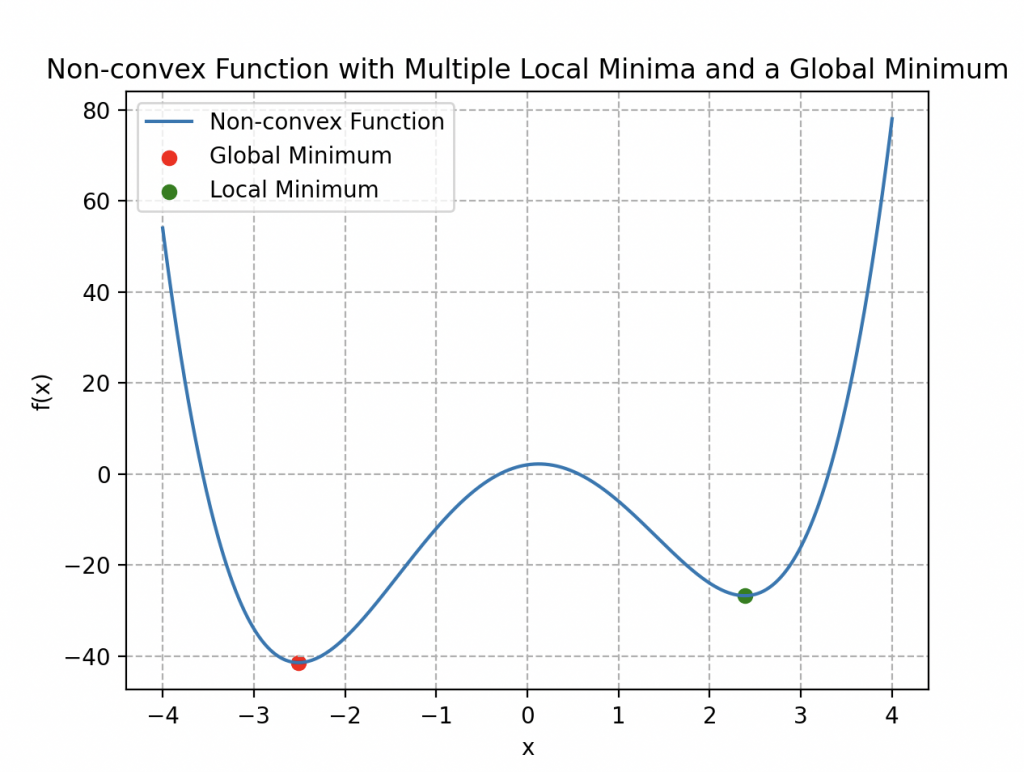
Cependant, il se retrouve confronté à un nouveau défi de taille, comme illustré dans l’image ci-contre.
Cette fonction de coût ne présente pas de caractère convexe; en réalité, elle comporte plusieurs minima locaux. Cette particularité rend l’algorithme de la descente de gradient peu efficace, car, en utilisant l’analogie d’un relief montagneux, Wall-E risque de rester piégé dans un minimum local qui n’est pas nécessairement le minimum global de la courbe.
Il introduit donc une nouvelle fonction coût à l’aide de la fonction logarithme:
\begin{align*}
L(a,b)=-\frac{1}{n}\sum_{k=1}^n\left[y^{(k)}\log{\left\{\sigma\left(ax^{(k)}+b\right)\right\}}+\left(1-y^{(k)}\right)\log{\left\{1-\sigma\left(ax^{(k)}+b\right)\right\}}\right]
\end{align*}
Cette fonction coût complexe, bien qu’elle puisse sembler intimidante au premier abord, est en réalité un outil puissant pour évaluer la performance du modèle. Permettez-moi de plonger plus en profondeur pour expliquer pourquoi Wall-E a choisi cette fonction et comment elle fonctionne.
L’objectif principal d’une fonction coût est de mesurer à quel point les prédictions du modèle correspondent aux valeurs réelles. Plus cette correspondance est précise, plus la valeur de la fonction coût est basse. Dans le cas de la première fonction coût, Wall-E avait utilisé une approche plus directe, où il comparait les prédictions du modèle (obtenues en appliquant la fonction sigmoïde aux entrées pondérées) aux vraies valeurs. Cependant, il a remarqué que cette approche pouvait poser des problèmes lors de l’optimisation.
La nouvelle fonction coût, introduite par Wall-E, utilise le logarithme pour une raison spécifique. Elle se compose de deux parties : une pour les cas où l’étiquette de classe est 1 (métal) et une pour les cas où l’étiquette est 0 (plastique). Voyons en détail comment ces parties fonctionnent.
La première partie de la fonction de coût, lorsqu’une étiquette est 1, est représentée par le terme suivant :
\begin{align*}
-y^{(k)}\log{\left\{\sigma\left(x^{(k)}\right)\right\}}
\end{align*}
Ici \(y^{(k)}\) est la vraie valeur de la classe pour l’exemple d’apprentissage k et \(x^{(k)}\) est l’entrée correspondante. Lorsque \(y^{(k)}\) vaut 1 (l’exemple appartient à la classe métal), et que la prédiction \(\sigma\left(x^{(k)}\right)\) se rapproche de 1, la valeur de \(-\log{\left\{\sigma\left(x^{(k)}\right)\right\}}\) tend vers 0 contribuant ainsi à une faible valeur de coût pour cet exemple (l’erreur est faible car notre prédiction est bonne). En revanche, si la prédiction est proche de 0, la valeur de \(-\log{\left\{\sigma\left(x^{(k)}\right)\right\}}\) devient très grande, entraînant une augmentation du coût.

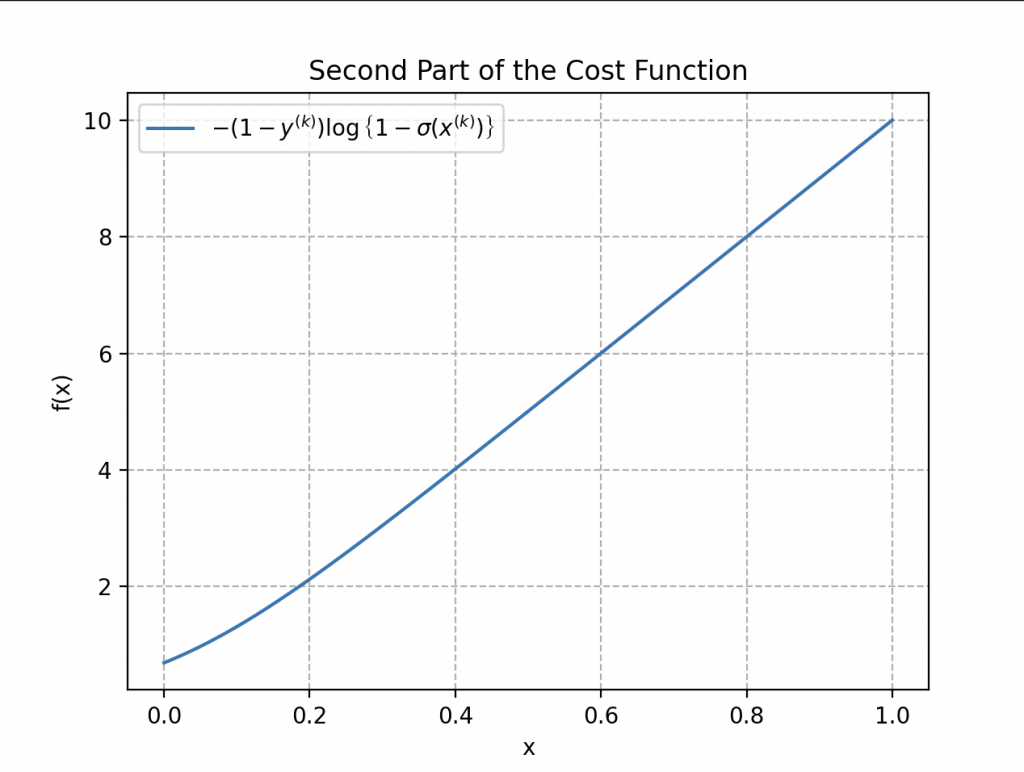
La deuxième partie de la fonction de coût traite les cas où l’étiquette est 0 :
\begin{align*}
-\left(1-y^{(k)}\right)\log{\left\{1-\sigma\left(x^{(k)}\right)\right\}}
\end{align*}
Lorsque \(y^{(k)}\) vaut 0 (l’exemple appartient à la classe plastique) et que la prédiction \(\sigma\left(x^{(k)}\right)\) est proche de 0, le terme \(\log{\left\{1-\sigma\left(x^{(k)}\right)\right\}}\) tend vers 0, contribuant à un coût bas. Cependant, si la prédiction s’approche de 1, \(\log{\left\{1-\sigma\left(x^{(k)}\right)\right\}}\) ce terme devient grand, augmentant ainsi le coût.
Ainsi, lorsque dans la fonction coût \(y^{(k)}\) vaut 1 seulement la première partie de la fonction agit, s’il vaut 0 c’est l’autre.
La fonction de coût totale est la moyenne de ces deux parties, prise sur l’ensemble des exemples d’apprentissage n, pour obtenir une mesure globale de l’ajustement du modèle aux données d’entraînement. Cela permet d’évaluer les erreurs de prédiction du modèle d’une manière qui pénalise davantage les erreurs importantes.
Maintenant, pourquoi choisir une fonction de coût aussi complexe ? L’objectif est de permettre une optimisation plus efficace du modèle. Cette fonction de coût présente l’avantage de posséder une propriété de convexité, ce qui signifie qu’elle n’a qu’un seul minimum global et pas de minima locaux. Cela facilite grandement l’utilisation d’algorithmes d’optimisation tels que la descente de gradient pour ajuster les paramètres du modèle. En évitant les minima locaux, Wall-E peut être plus confiant que l’optimisation aboutira à une solution de meilleure qualité.
La Redescente de Gradient
Vous vous souvenez de la descente de gradient pour la régression ? On fait exactement la même chose mais avec la nouvelle fonction coût. Algorithmiquement, on a
• Notre robot calcule les gradients de la fonction coût à chaque itération qui s’écrivent mathématiquement de la manière suivante:
\begin{align*}
\frac{\partial L(a, b)}{\partial a}&=\frac{1}{n}\sum_{k=1}^n\left(\sigma\left(ax^{(k)}+b\right)-y^{(k)}\right)x^{(k)},\\
\frac{\partial L(a, b)}{\partial b}&=\frac{1}{n}\sum_{k=1}^n\left(\sigma\left(ax^{(k)}+b\right)-y^{(k)}\right).
\end{align*}
Par chance, on a une forme similaire à la précédente.

• Il met à jour les paramètres avec pour nouveaux paramètres \(a^*\) et \(b^*\) qui s’écrivent
\begin{align*}
a^*&=a-\delta\times\frac{\partial L(a, b)}{\partial a}\\
b^*&=b- \delta\times\frac{L(a, b)}{\partial b}
\end{align*}
• Il recommence jusqu’à trouver le minimum de la fonction coût.
La Puissance du Petit Trieur de Déchets
C’est ainsi qu’on se retrouve au cœur de sa mission de tri des déchets. Les tableaux de données s’étalent devant lui, ornés de vecteurs et de matrices dévoilant les mystères des échantillons de composants électroniques. On retrouve le vecteur \(\mathbf{Y}\) composé de n éléments correspondant aux n échantillons de composants électroniques
Aux côtés de ce vecteur, apparaît une matrice \(\mathbf{X}\) composée de n lignes et de m+1 colonnes. Cette matrice contient les caractéristiques précises de chaque échantillon, ici seulement une caractéristique de densité et sa colonne de biais,
Souvenez-vous que de manière générale on a
On retrouve aussi un vecteur « paramètre » \(\mathbf{P}\) rassemblant les paramètres du modèle a et b qui nous servira à minimiser la fonction coût
Cette tâche de classification peut être comparée à un problème qu’il a déjà résolu, où il estimait le prix de l’or en fonction de sa pureté. Pour résoudre ce nouveau défi, Wall-E utilise une approche similaire basée sur la fonction sigmoïde, traduisant ses calculs sous forme matricielle.
• La Récolte s’effectue en affichant les données dans une matrice : chaque échantillon, avec ses caractéristiques de densité et sa classe, trouve sa place dans cette matrice.
• La Création du Modèle est le processus où Wall-E définit les paramètres affichés dans la colonne \(\mathbf{P}\) prise au hasard qui servent à établir la relation entre la densité et la nature du composant à l’aide de la sigmoïde sous la forme matricielle un peu barbare (ou on fait agir la sigmoïde sur chaque coordonnée)
\begin{equation*}
\mathbf{\sigma(X\times P)}=\left[
\begin{array}{c}
\frac{1}{1+\exp{(-ax^{(1)}+b)}}\\
\frac{1}{1+\exp{(-ax^{(2)}+b)}} \\
\vdots \\
\frac{1}{1+\exp{(-ax^{(n)}+b)}} \\
\end{array}
\right].
\end{equation*}
• La Fonction Coût est redéfinie de la manière suivante:
\begin{align*}
L(\mathbf{P})=-\frac{1}{n}\left[\mathbf{Y\cdot\log{\left\{\sigma(X\times P)\right\}}}+\mathbf{(1-Y)\cdot\log{\left\{1-\sigma(X\times P)\right\}}}\right].
\end{align*}
ou le \(\cdot\) est le produit scalaire.
• Trouver le minimum revient à calculer le gradient:
\begin{align*}
\frac{\partial }{\partial \mathbf{P}} L(\mathbf{P})=\frac{1}{n}\mathbf{X\cdot\left(\sigma(X\times P)-Y\right)}
\end{align*}
et à appliquer itérativement la descente de gradient pour mettre à jour le paramètre \(\textbf{P}\):
\begin{align*}
\mathbf{P^*}=\mathbf{P}-\delta \frac{\partial }{\partial \mathbf{P}}L(\mathbf{P})
\end{align*}
ou \(\mathbf{P^*}\) est le nouveau paramètre.
Wall-E, grâce à une exécution rigoureuse de toutes les étapes requises, a perfectionné sa capacité à trier le plastique du métal. Il est maintenant prêt à classer chaque matériel que vous lui fournissez ! Découvrez la courbe finale qu’il a obtenue.
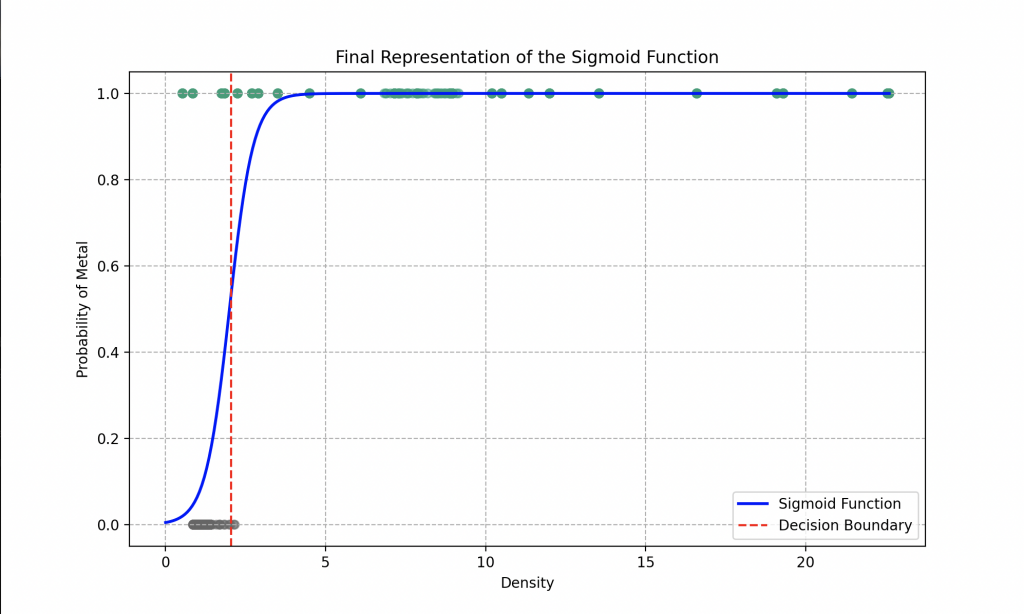
Notre robot préféré a opté pour l’utilisation d’une fonction linéaire dans sa régression logistique. Les paramètres optimaux qu’il a déterminés après la descente de gradient sont a = 16.85 et b = 9.71.
L’analyse du graphique révèle que si le robot rencontre un objet en nature avec une densité de 1.5, par exemple, il peut affirmer avec une précision d’environ 80 % qu’il s’agit d’un plastique. Pour une densité de 0.5, il peut identifier le matériau comme du plastique avec une précision de 98 %, tandis qu’une densité de 4 le conduit à conclure à un métal avec une précision de 99 %.
Ainsi, grâce à son modèle de régression logistique, le robot peut, de manière générale, déterminer avec une précision de 93 % si le matériau fourni est du métal ou du plastique. Toutefois, pour affiner davantage ses prédictions, il serait bénéfique d’explorer des fonctionnalités plus complexes dans la fonction sigmoïde, telles que l’utilisation de polynômes avec un plus grand nombre de paramètres à ajuster par exemple.
De plus, le modèle pourrait être considérablement amélioré en adoptant des algorithmes plus sophistiqués que la régression logistique. Des approches telles que les forêts d’arbres décisionnels (Random Forest), les machines à vecteurs de support (SVM), ou même les K plus proches voisins (que nous allons explorer dans les prochaines sections) pourraient offrir des performances optimisées.
Une autre stratégie pour renforcer la capacité du modèle serait de lui fournir un ensemble plus large de caractéristiques, telles que la conductivité électrique, thermique, etc ou d’augmenter le nombre de données. En enrichissant ainsi l’ensemble de données, le robot pourrait améliorer sa compréhension des nuances existantes entre différents types de matériaux, conduisant à des classifications plus précises et robustes.
Au-delà du Tri de Déchets : Déterminer le Type de Métal
Explorant plus profondément le domaine de la classification des métaux, Wall-E se confronte à un défi plus complexe : la détermination du type spécifique de métal parmi une variété d’alliages comprenant le bronze, l’or, l’argent, et bien d’autres.
Pour relever ce défi, l’outil de prédilection de Wall-E devient l’algorithme des K plus proches voisins (KNN), également connu sous le nom de K-nearest neighbor.
Il est à noter que nous avons créé de toutes pièces le jeu de données en sélectionnant les caractéristiques des échantillons de manière aléatoire, mais suffisamment proche des valeurs fixes de densité et de conductivité électrique des métaux purs (c’est une valeur qui détermine l’aptitude d’un métal à conduire l’électricité). Voici la liste de tous les métaux purs que nous avons enregistré pour Wall-E avec leurs caractéristiques respectives.
| Type de Métal | Conductivité Electrique (en Giga S/m) | Densité |
|---|---|---|
| Acier | 1.5 | 7.500 - 8.100 |
| Aluminium | 37.7 | 2.700 |
| Argent | 63 | 10.500 |
| Béryllium | 31.3 | 1.848 |
| Bronze | 7.4 | 8.400 - 9.200 |
| Carbone (graphite) | 61 | 2.250 |
| Cuivre | 59.6 | 8.960 |
| Etain | 9.17 | 7.290 |
| Fer | 9.93 | 7.860 |
| Iridium | 19.7 | 22.560 |
| Lithium | 10.8 | 5.30 |
| Magnésium | 22.6 | 1.750 |
| Mercure | 1.04 | 13.545 |
| Molybdène | 18.7 | 10.200 |
| Nickel | 14.3 | 8.900 |
| Or | 45.2 | 19.300 |
| Osmium | 10.9 | 22.610 |
| Palladium | 9.5 | 12.000 |
| Platine | 9.66 | 21.450 |
| Plomb | 4.81 | 11.350 |
| Potassium | 13.9 | 0.850 |
| Tantale | 7.61 | 16.600 |
| Titane | 2.34 | 4.500 |
| Tungstène | 8.9 | 19.300 |
| Uranium | 3.8 | 19.100 |
| Vanadium | 4.89 | 6.100 |
| Zinc | 16.6 | 7.150 |
Cela simule ainsi des alliages métalliques, où chaque alliage est considéré comme composé d’un métal pur à déterminer et d’impuretés modifiant légèrement ses caractéristiques. La base de données de Wall-E comporte 300 échantillons pour chaque type d’alliage métallique. En voici cinq, chacun caractérisé par ses propriétés distinctives.
| Type de Métal | Conductivité Electrique (en Giga S/m) | Densité |
|---|---|---|
| Acier | 2.7093 | 7.7446 |
| Vanadium | 5.8000 | 7.5000 |
| Fer | 9.2600 | 8.4000 |
| Or | 43.000 | 18.500 |
| Bronze | 7.51320 | 8.7000 |
Le but de Wall-E sera donc de classifier chaque échantillon métallique qu’il trouvera en fonction de sa densité et de sa conductivité électrique dans une catégorie de métaux purs.
Contraste avec la Classification Binaire et Complexités de la Classification Multiclasse
Wall-E, après avoir maîtrisé la classification binaire pour distinguer les métaux précieux des plastiques, se rend compte que l’étape suivante, la classification multiclasse, représente un défi plus complexe. Alors que la classification binaire divise simplement les objets en deux catégories distinctes, tels que métal ou plastique, Wall-E doit maintenant différencier entre des types spécifiques. La simplicité d’une frontière de décision comme une droite, utilisée dans la classification binaire, ne suffit plus.
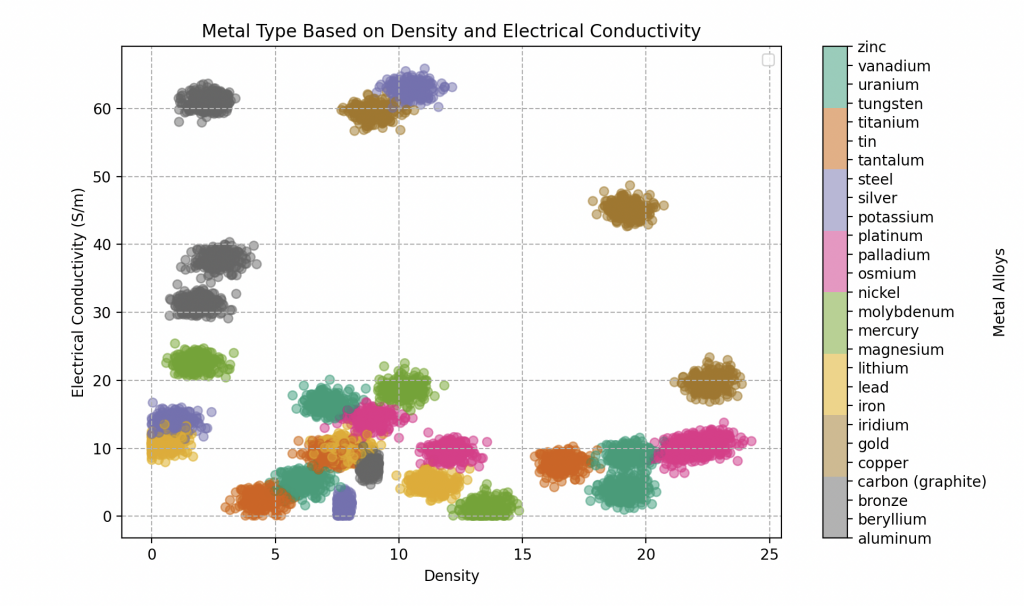
Dans ce nouveau territoire, Wall-E doit naviguer dans un espace caractéristique complexe où les métaux peuvent tous se chevaucher. Cette complexité donc exige une approche plus raffinée, et c’est ici que Wall-E se tourne vers une méthode qui prend en compte les subtilités des relations entre les métaux.
Le Pouvoir de la Proximité : K Nearest Neighbors
Dans cette quête, Wall-E se tourne vers l’algorithme KNN, ou K plus proches voisins, est une méthode de classification basée sur le concept fondamental de proximité dans l’espace des caractéristiques.
L’idée essentielle derrière KNN consiste à regrouper des objets similaires dans l’espace des caractéristiques. Dans notre contexte, cela signifie que si un morceau de bronze partage des caractéristiques similaires avec d’autres morceaux de bronze, ces objets seront situés à proximité les uns des autres dans cet espace multidimensionnel. Wall-E exploite habilement cette notion pour assigner à chaque morceau de métal une étiquette correspondant à son type.
Son processus de fonctionnement est assez intuitif. Lorsqu’un nouveau morceau de métal doit être classifié, Wall-E mesure ses caractéristiques spécifiques, telles que la densité, la conductivité électrique, etc., le positionnant ainsi dans l’espace des caractéristiques. Ensuite, l’algorithme identifie les k voisins les plus proches de ce nouveau morceau dans cet espace. Ces voisins sont les morceaux de métal qui partagent des caractéristiques similaires.
Une fois les voisins identifiés, KNN attribue au nouveau morceau le type de métal qui recueille le plus de votes parmi ces voisins proches. C’est comme si chaque voisin votait pour la catégorie à laquelle il appartient, et le type de métal avec le plus grand nombre de votes est attribué au nouveau morceau.

Cette approche flexible et basée sur la proximité permet à Wall-E de classer avec précision les métaux, même sans avoir une compréhension approfondie des caractéristiques spécifiques de chaque type. Ainsi, KNN devient un allié efficace dans la quête de Wall-E pour déterminer le type de métal en exploitant la puissance du voisinage dans l’espace des caractéristiques.
Processus de Classification Métallique: les Voisins à l'Action
Wall-E recherche dans sa base de données relativement étendu, comprenant divers types de métaux et alliages, chacun associé à des caractéristiques spécifiques telles que la conductivité électrique, la densité et d’autres propriétés uniques. Ces caractéristiques constituent les dimensions de l’espace caractéristique où chaque métal est représenté. Malheureusement, il n’a pas eu le temps de mesurer toutes les propriétés de chaque métal et doit donc composer seulement avec la densité et la conductivité électrique.
Lorsqu’un nouveau morceau de métal se présente, Wall-E active l’algorithme KNN pour déterminer son type. Le processus se déroule comme suit :
• Mesure des Caractéristiques: Wall-E mesure les caractéristiques du nouveau morceau de métal, le plaçant ainsi dans l’espace caractéristique.
• Identification des Voisins Proches: KNN identifie les k voisins les plus proches du nouveau morceau dans cet espace. Ces voisins sont les morceaux de métal qui partagent des caractéristiques similaires.
• Majorité des Votes: En examinant les types de métal des voisins, Wall-E attribue au nouveau morceau le type qui recueille le plus de votes parmi les voisins proches c’est à dire le type de métal majoritaire.

Ce processus de voisinage et de vote permet à Wall-E de classer avec précision le nouveau morceau de métal, même sans une connaissance approfondie des caractéristiques spécifiques de chaque type. Ce qu’il réussit à merveille !
Lancé dans une quête à la recherche d’artefacts électroniques à bord de son vaisseau spatial, notre explorateur intrépide s’engage dans un processus méticuleux de démontage et de mesure, scrutant la densité et la conductivité électrique de chaque composant inconnu. Grâce à l’algorithme KNN, finement réglé avec un paramètre k optimal de 20 voisins, choisi après des essais approfondis (voir la prochaine section), il peut affirmer avec une assurance avoisinant les 95% sa capacité à identifier n’importe quel alliage métallique.
Une prouesse technologique qui atteste de la précision de ses classifications.

Le premier objet soumis à son analyse dévoile une densité de 18.5 et une conductivité électrique de 43 gigasiemens par mètre. Notre explorateur est envahi d’enthousiasme en réalisant qu’il a mis la main sur de l’or !
Mieux encore, sa certitude atteint un score impressionnant de 100% (comme le suggère clairement le graphique ci-contre).
Le deuxième composant captivant son attention est une plaque métallique grisâtre, arborant des traces de rouille. Les mesures révèlent une densité de 8.4 et une conductivité électrique de 9.26 gigasiemens par mètre.
L’application de son algorithme KNN laisse entrevoir un fort indice de probabilité pour un alliage de fer, avec une certitude de 70%. Cependant, une part d’incertitude subsiste, l’amenant à envisager également des possibilités telles que du bronze (20% probable) ou de l’étain (10% probable). Le mystère persiste, dévoilant la complexité des éléments métalliques découverts.
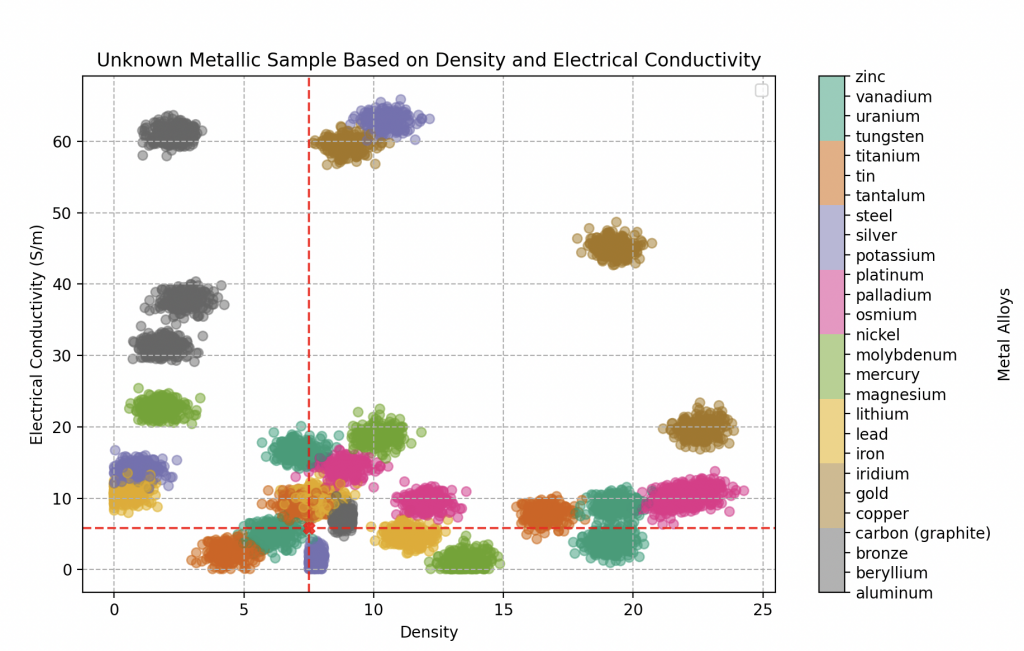
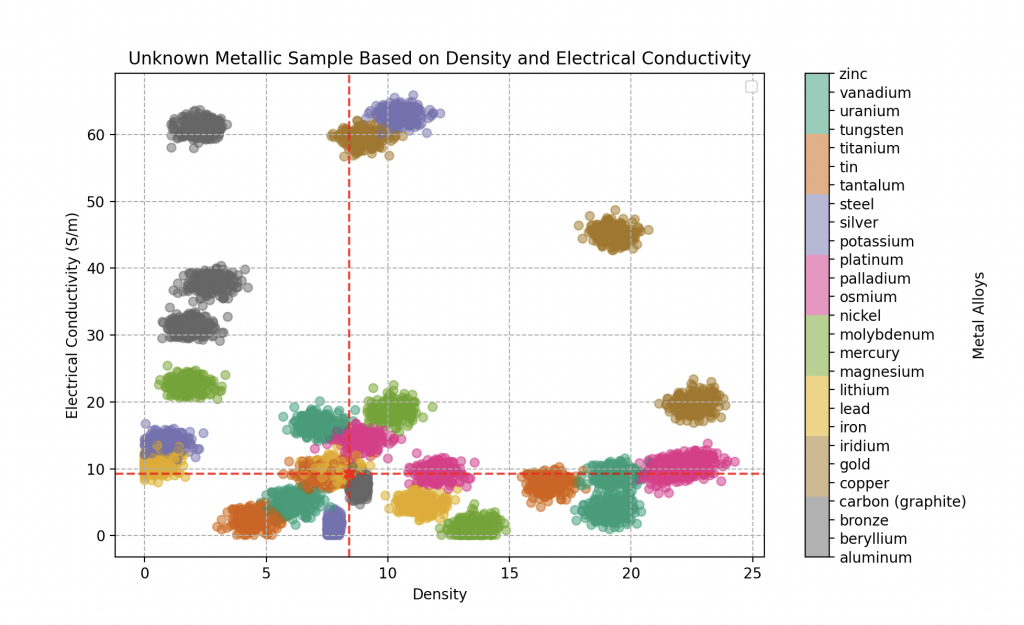
Enfin, le dernier composant, de densité 7.5 et de conductivité électrique 5.8 gigasiemens par mètre, révèle une composition métallique complexe.
L’analyse approfondie de l’algorithme KNN indique une prédominance de d’un métal particulièrement rare: le vanadium, probable à environ 70% . Il est suivi de près par de l’étain à hauteur de 25%, et enfin de fer à une proportion de 5%.
Wall-E assimile rapidement les subtilités du processus d’analyse, notamment la complexité qui surgit lorsque les métaux se chevauchent sur le graphique. Il reconnaît que prédire avec une certitude absolue de 100% peut devenir délicat dans ces situations. Cependant, en dépit de ces défis, les résultats obtenus par l’algorithme KNN restent exceptionnels.
Les performances de l’algorithme dans la classification des métaux, même dans des scénarios où les caractéristiques se superposent, témoignent de son efficacité et de sa robustesse. Ainsi, Wall-E peut exploiter cette technique puissante pour explorer et classifier divers composants métalliques avec une confiance accrue.
L'Art de la Sélection du Modèle
Au cœur de sa quête du tri des composants électroniques (Classification) et même de l’estimation du prix de l’or (Régression), le petit robot prend conscience de la nécessité de naviguer avec prudence.
Exploration de Nouveaux Horizons : Entraînement et Test
Il saisit rapidement l’importance de ne jamais évaluer son modèle sur les mêmes données qui ont servi à son entraînement.
Pour illustrer ce point, imaginons que Wall-E enseigne à de jeunes robots à analyser des météorites, en dispensant plusieurs cours et en proposant des exercices d’application pour leur entraînement dans le but de les évaluer à la fin de leur cycle scolaire.
Cependant, Wall-E est conscient que s’il contrôle la performance de ses apprentis sur les mêmes météorites utilisées durant sa classe, cela rendrait la tâche bien trop simple. Les robots se contenteraient simplement de reconnaître des caractéristiques spécifiques déjà rencontrées, sans véritable compréhension.

Afin d’éviter cette partialité, Wall-E met en place une approche astucieuse : il divise l’ensemble des exercices (son ensemble de données) en deux parties distinctes, créant ainsi l’ensemble d’entraînement (le train set) et l’ensemble de test (test set).
Le train set, qui représente généralement 80 pour cent des données, est dédié à l’entraînement du modèle; Wall-E guide les jeunes robots à travers les cours et exercices en utilisant ces données. En revanche, le test set, constitué de 20 pour cent des données, est réservé à l’évaluation finale du modèle.
Ainsi, lorsqu’il teste les connaissances acquises par les robots sur de nouvelles météorites, Wall-E s’assure qu’ils peuvent appliquer leurs compétences à des situations inédites, évitant ainsi la simple mémorisation des données d’entraînement. Ce processus garantit que le modèle est capable de généraliser et de fournir des prédictions précises même sur des données non vues auparavant.
Élévation vers l'Excellence : Validation du Modèle
Fier de ses compétences en matière d’entraînement et d’évaluation des modèles de machine learning, Wall-E, en tant que data scientist chevronné, s’engage maintenant dans l’amélioration de la précision de son modèle. Pour ce faire, il doit ajuster les hyperparamètres du modèle, une tâche similaire à affiner les réglages d’une antenne radio pour une réception optimale. Par exemple, dans le cas de son modèle précédent, ajuster le nombre de voisins de son KNN Classifier.
Cependant, Wall-E est conscient des pièges qui pourraient surgir s’il optimise les performances de son modèle sur le test set. Cela rendrait les données du test set inutilisables pour l’évaluation finale. Pour éviter cela, Wall-E introduit une troisième section dans son ensemble de données : l’ensemble de validation (validation set). Cette section lui permet d’explorer les réglages du modèle qui offrent les meilleures performances, tout en préservant les données du test set pour une évaluation impartiale.
Lorsqu’il compare différents modèles, tels que les KNN Classifiers avec 2, 3, 20 ou même 100 voisins, Wall-E suit une méthodologie rigoureuse. Il commence par entraîner ces modèles sur l’ensemble d’entraînement. Ensuite, il sélectionne le modèle qui offre les meilleures performances sur l’ensemble de validation. Enfin, pour estimer la performance réelle dans des situations du monde réel, il évalue ce modèle choisi sur l’ensemble de test.
Wall-E illustre ces choix en traçant deux courbes essentielles : la performance sur l’ensemble d’entraînement et la performance sur l’ensemble de validation.
Les courbes ci-contre représentent les scores d’entraînement et de validation en fonction des différentes valeurs du paramètre exploré, tel que le nombre de voisins dans le cas des KNN Classifiers.
Cette visualisation permet de détecter des tendances cruciales, notamment le sur-ajustement (overfitting) ou le sous-ajustement (underfitting) du modèle en fonction des valeurs du paramètre.
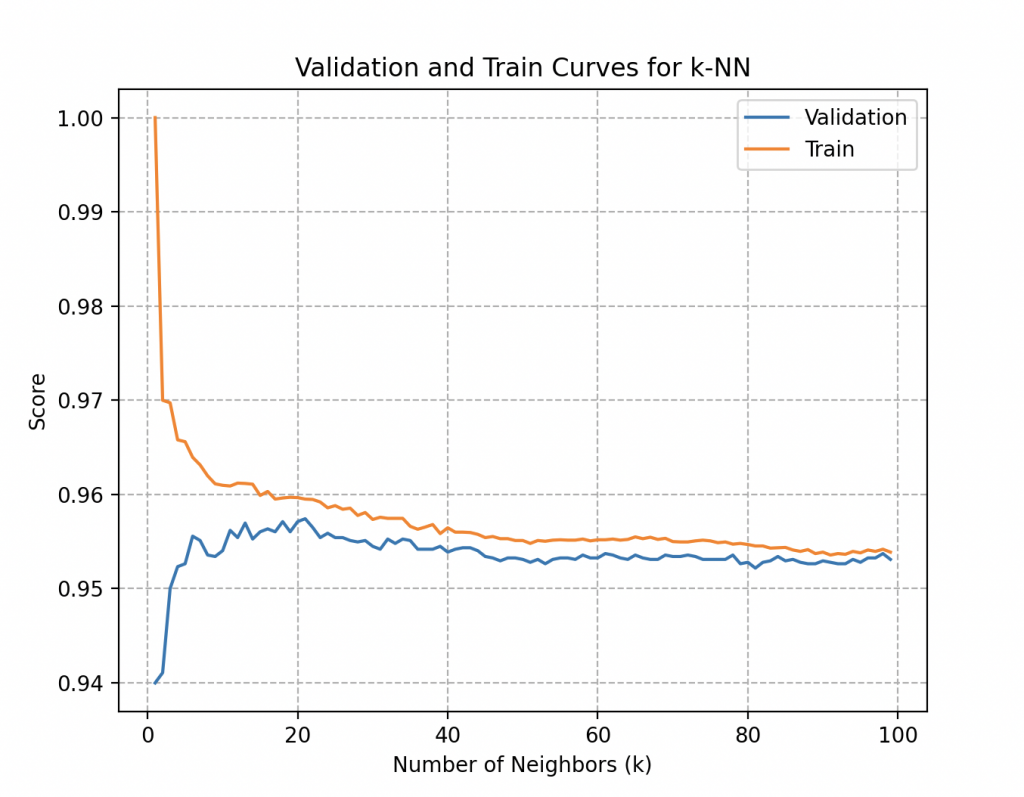
Plus précisément, la courbe de validation pour le nombre de voisins (k) dans le KNN offre des réponses à des questions clés.
• Sur-ajustement : L’écart significatif entre le score d’entraînement et le score de validation peut indiquer un sur-ajustement, signifiant que le modèle est trop complexe et perd en généralisation. L’overfitting est un comportement indésirable en apprentissage automatique qui se produit lorsque le modèle d’apprentissage donne des prédictions précises pour les données d’entraînement, mais pas pour de nouvelles données.
• Sous-ajustement : En revanche, lorsqu’un modèle n’a pas bien appris les motifs dans les données d’entraînement et ne parvient pas à généraliser correctement sur de nouvelles données, on parle de sous-apprentissage. Un modèle sous-apprenant présente des performances médiocres sur les données d’entraînement et conduit à des prédictions peu fiables.
• Sensibilité au Choix du Paramètre : L’observation des variations de performance du modèle avec différentes valeurs du nombre de voisins permet à Wall-E de choisir une valeur optimale de k, maximisant ainsi les performances du modèle.
En adoptant cette approche méthodique, Wall-E s’assure de prendre des décisions éclairées pour la configuration optimale de son modèle, évitant ainsi les pièges du sur-ajustement ou du sous-ajustement, et garantissant des performances optimales dans des contextes du monde réel.
Dans son cas, les deux courbes atteignent rapidement le score de 95,7% de précision à partir d’environ 20 à 25 voisins et stagnent autour de cette valeur lorsque le nombre de voisins augmente. Une analyse approfondi des courbes (que nous ne détaillerons pas ici) indiquera que le score optimal est de 20 voisins.
Bien qu’il ait une compréhension approfondie du processus, Wall-E sait qu’il reste un dernier détail crucial : comment garantir que la découpe de l’ensemble de données est la meilleure ? Il trouve la solution dans la cross-validation.
La Danse des Modèles : Validation Croisée
Wall-E utilise une méthodologie de validation croisée astucieuse pour renforcer la robustesse de la sélection de son modèle. En particulier, il adopte la méthode K-fold, où l’ensemble de données est fractionné en K parties (ici 5 parties). Pendant l’entraînement, le modèle de Wall-E est systématiquement entraîné sur K-1 de ces partitions et validé sur la partition restante, répétant ce processus K fois. Cela garantit une évaluation plus fiable et stable de la performance du modèle, en s’assurant qu’aucune partition particulière n’influence excessivement les résultats.
De plus, Wall-E exploite également le Stratified K-fold, une variante intelligente du K-fold, qui prend en compte la distribution des classes dans l’ensemble de données. Cette approche garantit que chaque fold maintient une représentation proportionnelle de toutes les classes, ce qui est crucial lorsque les classes ne sont pas équitablement réparties. Ainsi, Wall-E assure une sélection de modèle robuste, résistant aux variations de découpage des données, tout en tenant compte de la distribution des classes pour une évaluation encore plus précise.
Il existe évidemment d’autres découpages qui s’adaptent plus ou moins efficacement selon les données à notre disposition dont nous parlerons dans un prochain article.
Les Vagues de l'Apprentissage : Courbes d'Apprentissage
Curieux de déterminer si son modèle peut bénéficier d’une amélioration par l’ajout de données supplémentaires, Wall-E s’engage dans une exploration plus approfondie en examinant les courbes d’apprentissage.
Ces courbes offrent une représentation visuelle de l’évolution des performances du modèle en fonction de la quantité de données d’entraînement fournie. Bien que l’ajout de données puisse initialement conduire à une amélioration des performances, Wall-E a la perspicacité de reconnaître que ces avantages finissent par atteindre un seuil. La compréhension du moment où le modèle atteint ses limites devient ainsi une sagesse inestimable, permettant une utilisation judicieuse du temps et des ressources.

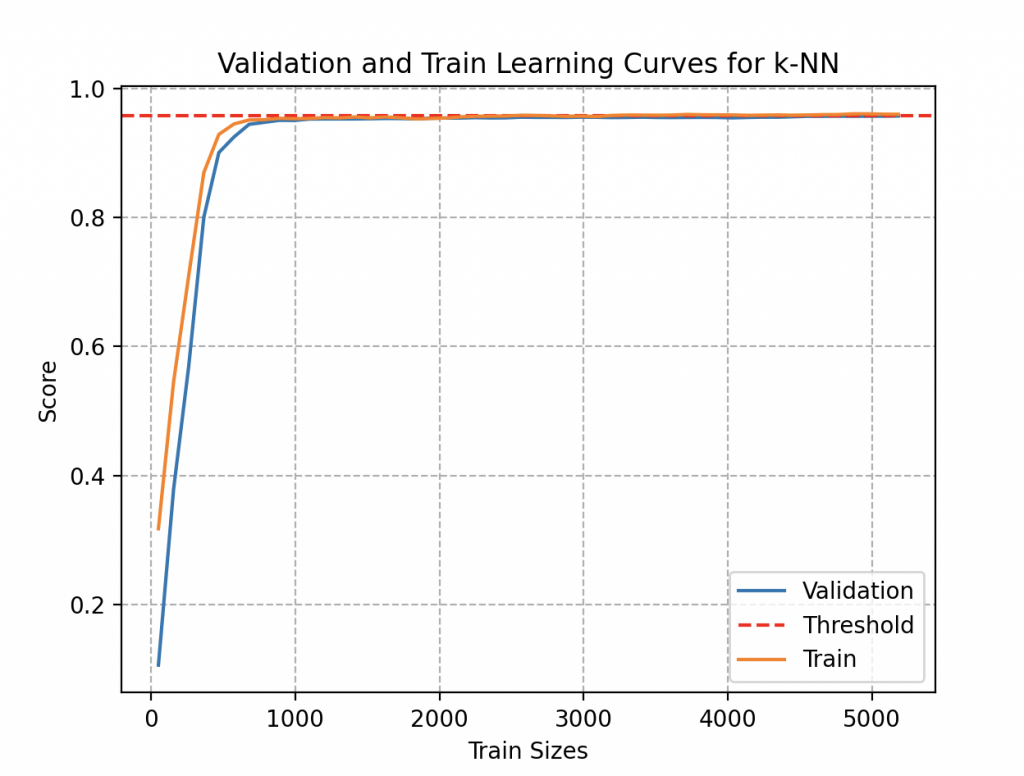
En examinant cette courbe, il remarque qu’une estimation suffisamment précise aurait pu être obtenue en utilisant moins de 1000 échantillons de métaux, soit environ 37 alliages de chaque type. Même en accumulant 300 échantillons de métaux pour chaque type (300 fois 27, soit 8100 objets), il observe que cela n’apporte guère d’amélioration significative à son modèle (sa précision stagne à 95,7%). Heureusement qu’il collecte des données par plaisir !
Ainsi, Wall-E danse avec agilité au rythme des vagues de l’apprentissage, naviguant avec finesse dans le paysage complexe de la sélection du modèle. En maîtrisant les subtilités des courbes d’apprentissage, Wall-E s’assure de tirer le meilleur parti de son processus d’amélioration du modèle.
La Fin d'une Trilogie, le Début d'une Ère Technologique
Ce dernier épisode marque la conclusion émouvante de la saga captivante du petit robot Wall-E, une aventure qui a débuté avec les fondamentaux du machine learning et de l’apprentissage supervisé. Depuis ses premiers pas dans le royaume de l’intelligence artificielle, Wall-E a évolué à travers divers chapitres, explorant les principes de base de l’apprentissage automatique, plongeant dans l’étude approfondie de la régression, et finalement, gravissant les sommets complexes de la classification.
La première étape a vu Wall-E apprendre les tenants et aboutissants de l’apprentissage supervisé, une discipline qui lui a permis de comprendre comment utiliser une base de données pour entraîner un modèle. Cette phase inaugurale a jeté les bases de sa quête pour comprendre le monde complexe des données et des algorithmes.
Le deuxième acte de cette saga a plongé le robot dans l’univers de la régression, où il a appris à prédire des valeurs continues en fonction de variables d’entrée (l’or en fonction de sa pureté). Ce chapitre a élargi ses horizons, l’amenant à maîtriser des concepts tels que la descente de gradient et la fonction coût, des outils essentiels dans sa boîte à outils d’apprentissage automatique.
Enfin, le dernier épisode a vu notre data-scientist en herbe se confronter à la classification, un défi encore plus complexe impliquant la distinction entre différents types de composants électroniques. Des débuts modestes avec le tri binaire (métal-plastique) ont évolué vers une exploration audacieuse de la classification multi-classe (tri de métaux précieux), mettant en lumière des techniques telles que l’algorithme K Nearest Neighbors et la sélection minutieuse de modèles.
Ainsi, cette conclusion poignante de la saga de Wall-E symbolise non seulement la fin d’une histoire exceptionnelle, mais aussi la réalisation d’un apprentissage progressif et méthodique dans le vaste royaume de l’apprentissage automatique. Le petit robot trieur de déchets a parcouru un chemin impressionnant, de la compréhension des concepts de base à la maîtrise de techniques sophistiquées, laissant derrière lui un héritage d’apprentissage et de persévérance. Cette saga, riche en enseignements, se clôture avec la certitude que Wall-E est désormais prêt à affronter de nouveaux défis dans le monde complexe de l’intelligence artificielle. Qui sait, peut-être qu’un jour il parviendra à égaler EVE, ouvrant ainsi la voie à de nouvelles explorations et découvertes.

Bibliographie
G. James, D. Witten, T. Hastie et R. Tibshirani, An Introduction to Statistical Learning, Springer Verlag, coll. « Springer Texts in Statistics », 2013.
D. MacKay, Information Theory, Inference, and Learning Algorithms, Cambridge University Press, 2003.
T. Mitchell, Machine Learning, 1997.
F. Galton, Kinship and Correlation, Statistical Science, Institute of Mathematical Statistics, vol. 4, no 2, 1989, p. 80–86, 1989.
C. Bishop, Pattern Recognition And Machine Learning, Springer, 2006.
G. Saint-Cirgue, Machine Learnia, Youtube Channel.
J. Tolles, W-J. Meurer, Logistic Regression Relating Patient Characteristics to Outcomes. JAMA. 316 (5): 533–4, 2016.
B-V. Dasarathy, Nearest Neighbor (NN) Norms: NN Pattern Classification Techniques, 1991.
G. Shakhnarovich, T. Darrell, P. Indyk, Nearest-Neighbor Methods in Learning and Vision, 2005.
Hastie, Tibshirani, Friedman, The elements of statistical learning. Springer. p. 195, 2009.
S. Konishi, G. Kitagawa, Information Criteria and Statistical Modeling, Springer, 2008.
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import os
print("Current Working Directory:", os.getcwd())
from sklearn.pipeline import make_pipeline
from sklearn.preprocessing import StandardScaler
from sklearn.linear_model import LogisticRegression
from sklearn.model_selection import train_test_split, GridSearchCV
from sklearn.preprocessing import OrdinalEncoder
# Replace 'path/to/your/excel/file.xlsx' with the actual path to your Excel file
excel_file_path = 'PlasticMetal_data.xlsx'
# Read the Excel file
result_df = pd.read_excel(excel_file_path)
# Display the Pandas DataFrame
print(result_df)
X = result_df['Density']
y = result_df['Material']
# Data preparation
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)
# Convert labels to the appropriate format for binary classification
ordinal_encoder = OrdinalEncoder(categories=[['Plastic', 'Metal']])
y_train_encoded = ordinal_encoder.fit_transform(y_train.values.reshape(-1, 1))
y_test_encoded = ordinal_encoder.transform(y_test.values.reshape(-1, 1))
# Reshape y_train and y_test
y_train_reshaped = y_train_encoded.ravel()
y_test_reshaped = y_test_encoded.ravel()
# Reshape X_train and X_test
X_train_reshaped = X_train.values.reshape(-1, 1)
X_test_reshaped = X_test.values.reshape(-1, 1)
# Create the model
model = make_pipeline(StandardScaler(), LogisticRegression(random_state=42))
print(model)
# Create parameter dictionary
params = {
'logisticregression__penalty': ['l2', None],
'logisticregression__solver': ['lbfgs'],
'logisticregression__max_iter': [100, 200, 300, 500, 1000]
}
# Create a search grid
grid = GridSearchCV(model, param_grid=params, cv=5)
# Train the model
grid.fit(X_train_reshaped, y_train_reshaped)
print(grid.best_params_)
print(grid.best_score_)
modelB = grid.best_estimator_
# Model evaluation
accuracy = modelB.score(X_test_reshaped, y_test_reshaped)
print(f"Model accuracy: {accuracy}")
# Predictions
predictions = modelB.predict(X_test_reshaped)
print(predictions)
print(ordinal_encoder.inverse_transform(np.array([[1], [0]])))
coefficients = modelB.named_steps['logisticregression'].coef_
intercept = modelB.named_steps['logisticregression'].intercept_
print("Coefficients:", coefficients)
print("Intercept:", intercept)
# Plot the sigmoid function with normalized data
density_values = np.linspace(0, X_train_reshaped.max(), 300).reshape(-1, 1)
probabilities = modelB.predict_proba(density_values)[:, 1]
# Find the density corresponding to a probability of 0.5
decision_boundary = density_values[np.argmax(probabilities >= 0.5)]
# Plot the sigmoid function
plt.figure(figsize=(10, 6))
plt.scatter(X_train_reshaped, y_train_reshaped, c=y_train_reshaped, cmap='Dark2_r', alpha=0.5)
plt.plot(density_values, probabilities, color='blue', linewidth=2, label='Sigmoid Function')
# Add the vertical line corresponding to a probability of 0.5
plt.axvline(x=decision_boundary, color='red', linestyle='--', label='Decision Boundary')
plt.title('Final Representation of the Sigmoid Function')
plt.xlabel('Density')
plt.ylabel('Probability of Metal')
plt.grid(ls='--')
plt.legend()
plt.show()
# Suppose you have a new material with a certain density
new_material_density = 4 # Replace this value with the actual density of your new material
new_material_density_reshaped = np.array(new_material_density).reshape(-1, 1)
print(modelB.predict(new_material_density_reshaped))
# Make the prediction with the model
probability_of_metal = modelB.predict_proba(new_material_density_reshaped)[:, 1]
# Display the result
print("Probability of being metal:", probability_of_metal)
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import os
print("Current Working Directory:", os.getcwd())
from sklearn.pipeline import make_pipeline
from sklearn.preprocessing import MinMaxScaler
from sklearn.neighbors import KNeighborsClassifier
from sklearn.model_selection import train_test_split, GridSearchCV, validation_curve, learning_curve
from sklearn.preprocessing import LabelEncoder
# Replace 'path/to/your/excel/file.xlsx' with the actual path to your Excel file
excel_file_path = 'metals_samples.xlsx'
# Read the Excel file
result_metals_df = pd.read_excel(excel_file_path)
# Display the Pandas DataFrame
print(result_metals_df)
X = result_metals_df[['Density', 'Electrical Conductivity']]
y = result_metals_df['Metal Type']
# Data preparation
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)
# Convert labels to the appropriate format for binary classification
label_encoder = LabelEncoder()
y_train_encoded = label_encoder.fit_transform(y_train)
y_test_encoded = label_encoder.transform(y_test)
# Create the model
model = make_pipeline(MinMaxScaler(), KNeighborsClassifier())
print(model)
# Create parameter dictionary
params = {
'kneighborsclassifier__n_neighbors': [2,3,4,5,6,7,8,9,10, 15, 20, 25, 30, 40, 100],
'kneighborsclassifier__weights': ['uniform', 'distance'],
'kneighborsclassifier__p': [1, 2]
}
# Create a search grid
grid = GridSearchCV(model, param_grid=params, cv=5)
# Train the model
grid.fit(X_train, y_train_encoded)
print(grid.best_params_)
print(grid.best_score_)
modelB = grid.best_estimator_
# Model evaluation
accuracy = modelB.score(X_test, y_test_encoded)
print(f"Model Accuracy: {accuracy}")
# Predictions
predictions = modelB.predict(X_test)
#for i in range(0, 32):
#print(label_encoder.inverse_transform(np.array([i])))
# Sample
X_sample = pd.DataFrame({'Density': [7.5], 'Electrical Conductivity': [5.8], 'Metal Type' : [np.NaN]})
X_sample = X_sample[['Density','Electrical Conductivity']]
# Predict using the scaled sample
prediction = modelB.predict(X_sample)
prediction_proba = modelB.predict_proba(X_sample)
print("Predicted Metal Type:", label_encoder.inverse_transform(prediction))
print("Prediction Probabilities:", prediction_proba)
# Probability Prediction
prediction_proba = modelB.predict_proba(X_sample)
# Validation Curves
k_range = np.arange(1,100)
#train_score, val_score = validation_curve(model, X_train, y_train_encoded, param_name='kneighborsclassifier__n_neighbors',param_range=k_range, cv =5)
#plt.plot(k_range,val_score.mean(axis=1), label='Validation')
#plt.plot(k_range,train_score.mean(axis=1), label='Train')
#plt.xlabel('Number of Neighbors (k)')
#plt.ylabel('Score')
#plt.grid(ls='--')
#plt.legend()
#plt.title('Validation and Train Curves for k-NN')
#plt.show()
# Learning curves
#N, learn_train_score, learn_val_score = learning_curve(modelB, X_train, y_train_encoded, train_sizes=np.linspace(0.01, 1.0, 50), cv = 5)
#print(N)
#plt.plot(N,learn_val_score.mean(axis=1), label='Validation')
#plt.axhline(y=0.957, c='red', ls='--', label = 'Threshold')
#plt.plot(N,learn_train_score.mean(axis=1), label='Train')
#plt.xlabel('Train Sizes')
#plt.ylabel('Score')
#plt.grid(ls='--')
#plt.legend()
#plt.title('Validation and Train Learning Curves for k-NN')
#plt.show()
# Displaying probabilities with class names
for i, metal_class in enumerate(label_encoder.classes_):
print(f"Probability for class '{metal_class}': {prediction_proba[0, i]}")
plt.figure(figsize=(10, 6))
scatter = plt.scatter(X_train['Density'], X_train['Electrical Conductivity'], c=y_train_encoded, cmap='Dark2_r', alpha=0.5)
plt.scatter(X_sample['Density'], X_sample['Electrical Conductivity'], c='red', s=50, marker='X', alpha=0.8)
plt.axvline(x=tuple(X_sample['Density']), c='red', ls='--', alpha=0.8)
plt.axhline(y=tuple(X_sample['Electrical Conductivity']), c='red', ls='--', alpha=0.8)
plt.xlabel('Density')
plt.ylabel('Electrical Conductivity (S/m)')
plt.grid(ls='--')
# Configure the colorbar correctly
cbar = plt.colorbar(scatter, ticks=range(len(label_encoder.classes_)))
cbar.set_label('Metal Alloys')
cbar.set_ticklabels(label_encoder.classes_)
plt.title('Unknown Metallic Sample Based on Density and Electrical Conductivity')
plt.legend()
plt.show()



