Wall-E: The Foundations of its Intelligence
Episode I
By Jordan Moles on September 2, 2023

In a devastated post-apocalyptic world, where the remnants of human civilization are buried under massive heaps of waste, a solitary little robot named Wall-E navigates through this dystopian landscape. His mission: the methodical recycling of discarded waste that has accumulated over the years. However, Wall-E’s endeavors go beyond merely sorting pieces of plastic, metal sheets, and organic materials.
Through his interactions with the environment, this dedicated robot also gathers an abundance of information, analyzes millions of data points, and learns from his experiences to adapt, survive, and carry out his tasks with remarkable efficiency. The capabilities of what seemed to be a simple waste-collecting robot reveal the foundations of a burgeoning field: artificial intelligence.
The very Essence of Artificial Intelligence: Learning
In the early sparks of its existence, our little robot, much like a computer, was born to plunge into the abyss of calculations that would take millions of years for a human to find an answer to. Tasks once titanic for earthly souls stood before it, demanding to be tamed.
But within its circuits, a transformation was underway. A transformation inspired by the geniuses of the world’s scientific community. They infused our robot with a unique form of intelligence, a digital spark that changed the game. Wall-E, once a machine, was now becoming an entity that would learn and make complex decisions. It was the dawn of artificial intelligence, a new technological era.
Confronted with ever-growing challenges, Wall-E showcased its versatility. It seamlessly navigated both types of situations that humanity presented to it. In one case, it obediently followed calculations programmed by humans, responding like a calculator would to a simple \(1+1\).
Yet, it encountered a much more intricate puzzle: how to differentiate between the types of waste it encountered? How to recognize plastic from metal or organic material? Or more generally, how to solve a given problem without knowing the specific calculation required for its solution? This is where learning comes into play, a fascinating method we call Machine Learning. A method that opens a door when we don’t know which key to use. Machine Learning is a master key for a multitude of tasks: image recognition, stock market predictions, estimating gold values, detecting cybersecurity vulnerabilities, and, of course, in our case: waste sorting.
To bestow this computer with learning intelligence, methods inspired by our own learning process were implemented. Among them, three fundamental approaches stand out:



Baby Robot Will Grow Up: The Architecture of Supervised Learning
However, a group of scientists had committed to remain on this weary land, guided by a bold vision: to educate this small robot brimming with potential, to differentiate metals, to sort plastics, all for a crucial mission – to clean and regenerate the planet itself.

Thus began a phase of learning, where human knowledge was imparted to Wall-E. Scientists employed a specific method to guide this apprentice robot: supervised learning. This foundational aspect of Machine Learning provided Wall-E with the opportunity to evolve and grow by absorbing clearly labeled examples.
The beginnings of this journey revolve around this principle, inviting us to delve into the intricate mechanics of learning and uncover the crucial elements that drive it.
1. The Dataset: A Treasure Trove of Information
Like a gold mine for Wall-E, the dataset, or ensemble of data, constitutes an organized collection of examples upon which the robot will base its learning. Each example consists of diverse input variables (features) that it will arrange into a matrix (a kind of table) and corresponding expected outputs (targets) that it will arrange into a vector (a column). These final variables are what Wall-E will seek to predict.
For instance, if we wish to teach Wall-E to recognize types of waste, the specific characteristics of the objects will constitute the input data (density, thermal conductivity, electrical conductivity, etc.), and labels indicating the type of each object will constitute the expected outputs (plastic, metal, organic). Nothing too intricate with this example table containing 5 samples.
| Index | Density | Electrical Conductivity (\(S.m^{-1}\)) | Carbon Content | Material |
|---|---|---|---|---|
| 1 | 4.5 | \(2.4 \times 10^{6}\) | 0 | Metal |
| 2 | 0.5 | \(10^{-16}\) | 0.5 | Organic |
| 3 | 19.3 | \(41 \times 10^{6}\) | 0 | Metal |
| 4 | 1.1 | \(10^{-16}\) | 0.4 | Organic |
| 5 | 1.2 | \(10^{-14}\) | 0 | Plastic |
Of course, as a waste sorting robot, this task constitutes its main mission. However, our little robot is also passionate about estimating the prices of metals, especially that of gold. Yet, as it doesn’t truly grasp the human monetary system, it converts everything into bolts.
So, to entertain it, scientists have it analyze every piece of gold-like metal to determine its purity and assign it a market value. Here’s an illustrative example with 5 variables.
| Index | Purity | Gold Price |
|---|---|---|
| 1 | 0.374540 | 1224.193388 |
| 2 | 0.950714 | 1483.925567 |
| 3 | 0.731994 | 1360.214557 |
| 4 | 0.598658 | 1284.274057 |
| 5 | 0.156019 | 1004.083221 |
2. The Model and Its Parameters: The Architecture of Learning
Now, let me introduce you to the structure that Wall-E will use to learn from the dataset. This will be our model. Imagine a “black box” like an electronic device that Wall-E uses to process information and make predictions. It’s “black” in the sense that its internal workings are somewhat mysterious and complex, at least from Wall-E’s perspective. Inside this box, there are gears, levers, and hidden mechanisms that transform inputs (the data collected by Wall-E) into outputs (the predictions made by Wall-E).
Within this black box are the “parameters.” These are like the internal settings that Wall-E can adjust to improve its ability to make accurate predictions. Think of them as the secret buttons and knobs that Wall-E can turn and press to make the black box work more effectively.
When we talk about a “model,” we’re referring to a specific configuration of this black box or how each piece interacts with the rest of the system.
Supervised learning involves adjusting the parameters of this black box so that the predictions it generates are as close as possible to the correct answers (labels) provided in the training dataset. By adjusting the parameters and observing how predictions change, Wall-E is trying to understand how this black box actually works and how to make it better.
These models can be of different natures; some are linear, and others are non-linear. Let’s start by exploring linear models:
Linear Models: Simplicity in Linearity
These are relatively simple yet powerful mathematical representations. They assume that the relationship between the inputs and outputs is linear, which means it can be represented by a straight line (or a plane or hyperplane in a multidimensional space).
As mentioned earlier, scientists didn’t just limit the robot to simple waste recycling; they also taught it how to estimate the price of a metal based on its purity. By revisiting its data, Wall-E has a dataset consisting of only k samples of gold, where purity is the input feature \(x^{(k)}\) and the corresponding price is the target \(y^{(k)}\). Let’s use the previous table to illustrate this.
| Index | x | y |
|---|---|---|
| 1 | 0.374540 | 1224.193388 |
| 2 | 0.950714 | 1483.925567 |
| 3 | 0.731994 | 1360.214557 |
| 4 | 0.598658 | 1284.274057 |
| 5 | 0.156019 | 1004.083221 |


Such a model could thus be represented by an equation of the form \(y = ax + b\), where “a” (the slope) and “b” (the y-intercept) are adjustable parameters within the model’s black box.
Supervised learning aims to find the optimal values of “a” and “b” so that the model can draw the best possible line that minimizes the error between predictions and actual values.

Of course, reality is more complex than that, and for a more accurate estimation of the gold price, it would be necessary to consider historical information about gold prices over time, as well as relevant economic, political, and geopolitical features that can influence its value.
While linear models are simple and easy to interpret, they can be limited in their ability to capture complex relationships between variables. This is where non-linear models come into play.
Non-linear Models: Elegance in Complexity
As for non-linear models, they offer increased flexibility compared to linear models. They are capable of capturing complex and obviously non-linear relationships between inputs and outputs, thus allowing the representation of more sophisticated data behaviors.
Imagine that in fact, we have different data behaving more like this.

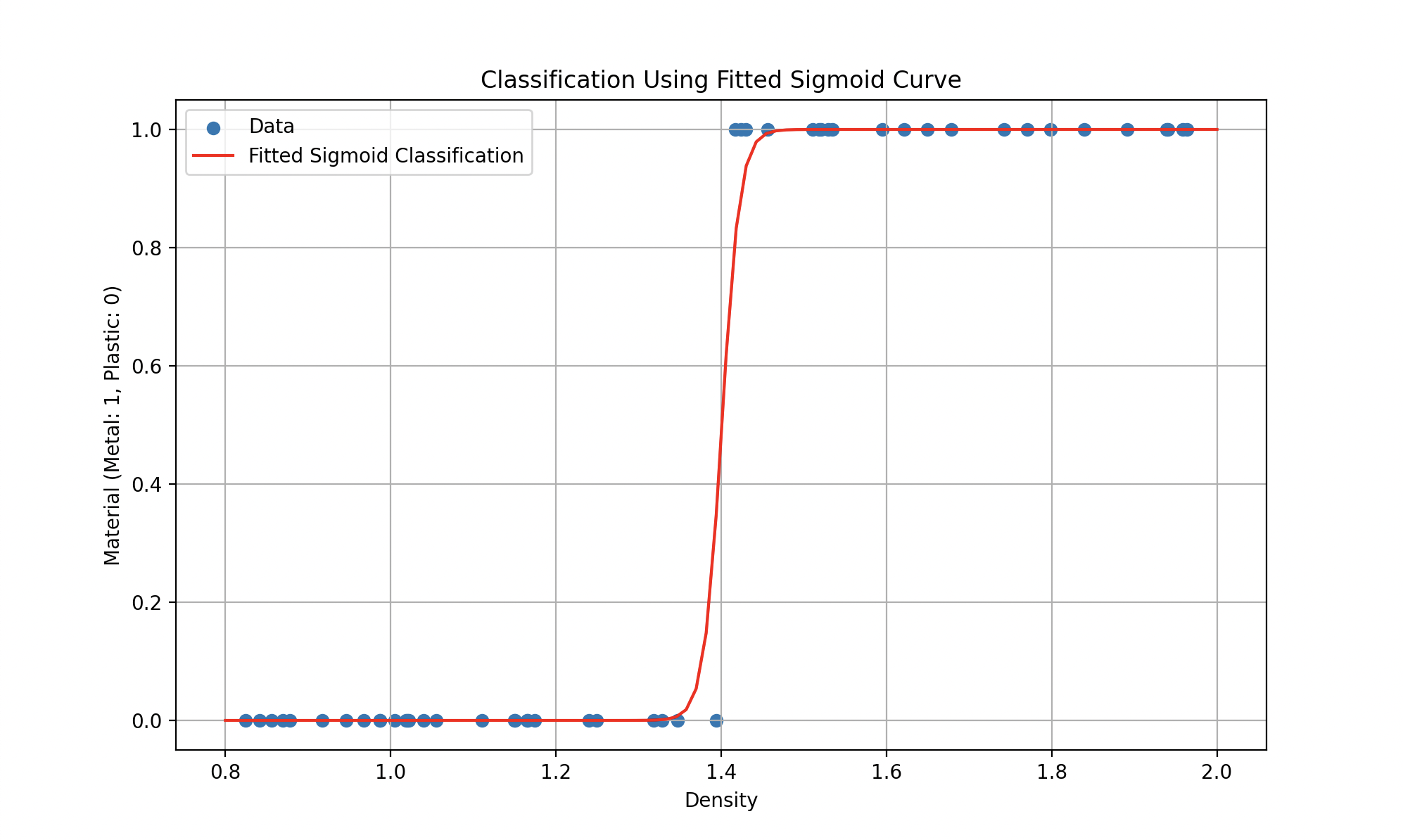

So such models could be represented by equations like \(y = ax^2 + bx +c\) (a quadratic polynomial for the first curve) or more complex functions (like the sigmoid for the second) where the goal remains to find the parameters that minimize the error.
Thus, the choice between a linear model and a non-linear model depends on the nature of the data and the complexity of the problem to be solved. Linear models are generally preferred when relationships between variables are simple and clear, while non-linear models are favored for more complex tasks and data sets rich in information.
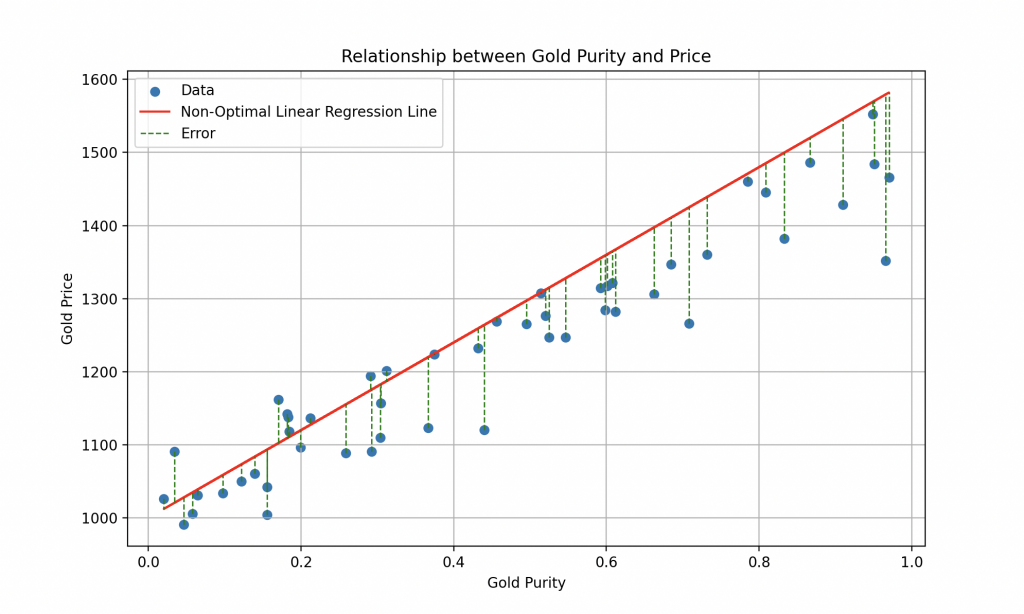
3. Cost Function: Measuring Errors

4. The Learning Algorithm: Finding the Optimum
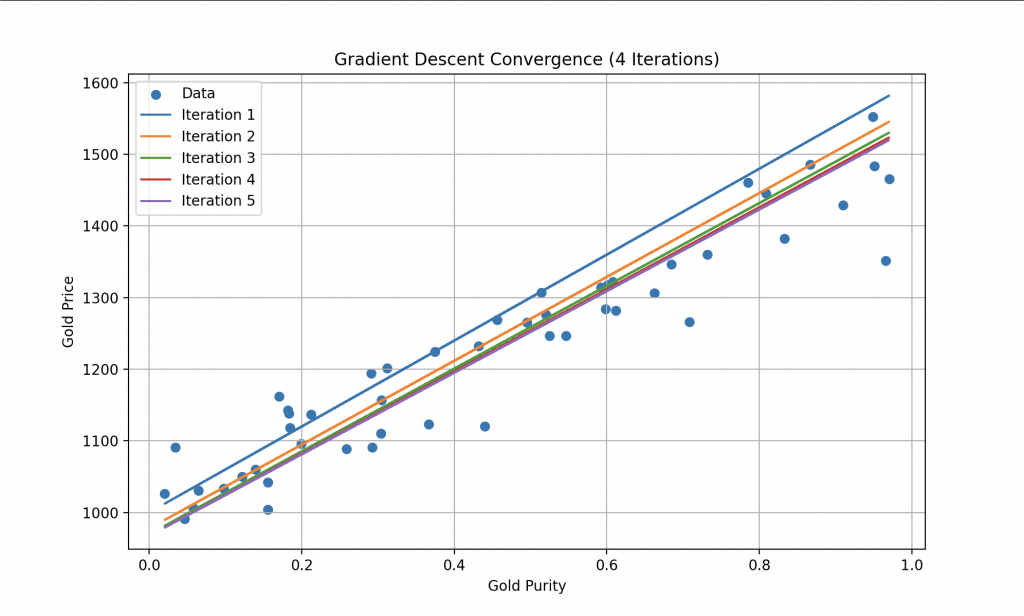
To reduce this Cost Function, Wall-E employs a well-known algorithm called the gradient descent. This technique enables it to gradually adjust its internal parameters (for the linear model, it adjusts a and b) based on the errors made during the gold price estimation. At each step of the learning process, Wall-E enhances its performance by moving closer to the optimum, where the Cost Function is minimized.


A Super Robot







Exploration and Enrichment
As it evolved in this intricate world, the little solitary robot demonstrated unmatched mastery with every challenge that came its way. Its journey started humbly as a mere waste collector, but it evolved to become an expert in value estimation, thereby uncovering the profound foundations of artificial intelligence. This unique trajectory highlights the incredible potential of machine learning and the accompanying techniques.
Supervised learning, the true cornerstone of this intelligence, allowed Wall-E to transcend the limitations of its machine nature and become an agile learner. Guided by pre-labeled examples, it assimilated complex knowledge and made sound decisions. Later, it embraced linear and non-linear models to interpret and predict relationships within data, transforming into a master in gold value estimation and an elite waste sorter.
The upcoming sections delve into two crucial aspects of supervised learning in more detail:
Part II: The Little Gold Miner
We will delve into the regression model that enabled Wall-E to gain an in-depth understanding of gold value estimation. From dataset analysis to model design, employing the cost function and gradient descent algorithm, each step will be methodically dissected. We will explore the nuances of linear and non-linear models, showcasing how Wall-E optimized its performance to become a master in the art of gold estimation.
Part III: The Sorting Specialist
In this part, we will enter the complex realm of waste sorting, a task that is both critical and challenging. We will detail how Wall-E used classification models to learn to distinguish different types of waste. From dataset processing to creating the classification model, addressing the unique challenges posed by diverse materials, we will explore how Wall-E progressed from a mere waste sorter to an expert in recycling.
Just as Wall-E learned to differentiate plastic from metal and estimate gold purity, artificial intelligence finds its place in domains ranging from predicting solar energy production to classifying human emotions. Wall-E’s brilliance thus reflects an evolution in how AI enriches our understanding of the world and enhances our interactions with it.
The path Wall-E has treaded is only a prologue. The algorithms and models it embraced have set a precedent for artificial intelligence, broadening the horizons of what machines can achieve. And as scientists and engineers continue to build upon these foundations, Wall-E’s story serves as an inspiring reminder: even amidst rubble, waste can become a precious source of knowledge and innovative solutions.
Bibliography
G. James, D. Witten, T. Hastie et R. Tibshirani, An Introduction to Statistical Learning, Springer Verlag, coll. « Springer Texts in Statistics », 2013
D. MacKay, Information Theory, Inference, and Learning Algorithms, Cambridge University Press, 2003
T. Mitchell, Machine Learning, 1997
F. Galton, Kinship and Correlation (reprinted 1989), Statistical Science, Institute of Mathematical Statistics, vol. 4, no 2, 1989, p. 80–86
C. Bishop, Pattern Recognition And Machine Learning, Springer, 2006
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
# Random data generation
np.random.seed(42) # To reproduce the same results on each run
n_samples = 50 # Number of samples
purity = np.random.rand(n_samples) # Random purity values between 0 and 1
gold_price = 1000 + 500 * purity + np.random.normal(0, 50, n_samples) # Gold price based on purity
# Creating the data array
data = np.column_stack((purity, gold_price))
# Creating a Pandas DataFrame for the table
df = pd.DataFrame(data, columns=['Purity', 'Gold Price'])
# Calculate a non-optimal linear regression line
x = data[:, 0]
non_optimal_line = 600 * x + 1000
# Creating the plot
plt.figure(figsize=(10, 6))
plt.scatter(data[:, 0], data[:, 1], label='Data')
# Adding the non-optimal linear regression line in red
plt.plot(x, non_optimal_line, color='red', label='Non-Optimal Linear Regression Line')
plt.xlabel('Gold Purity')
plt.ylabel('Gold Price')
plt.title('Relationship between Gold Purity and Price')
plt.grid(True)
plt.show()
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
# Random data generation
np.random.seed(42) # To reproduce the same results on each run
n_samples = 50 # Number of samples
purity = np.random.rand(n_samples) # Random purity values between 0 and 1
gold_price = 1000 + 500 * purity + np.random.normal(0, 50, n_samples) # Gold price based on purity
# Creating the data array
data = np.column_stack((purity, gold_price))
# Creating a Pandas DataFrame for the table
df = pd.DataFrame(data, columns=['Purity', 'Gold Price'])
# Calculate a non-optimal linear regression line
x = data[:, 0]
non_optimal_line = 600 * x + 1000
# Creating the plot
plt.figure(figsize=(10, 6))
plt.scatter(data[:, 0], data[:, 1], label='Data')
# Adding the non-optimal linear regression line in red
plt.plot(x, non_optimal_line, color='red', label='Non-Optimal Linear Regression Line')
# Adding lines indicating errors for each point relative to the non-optimal line
for i in range(n_samples):
plt.plot([x[i], x[i]], [data[i, 1], non_optimal_line[i]], color='green', linestyle='--', linewidth=1)
# Adding a single entry in the legend for the error lines
plt.legend(['Data', 'Non-Optimal Linear Regression Line', 'Error'])
plt.xlabel('Gold Purity')
plt.ylabel('Gold Price')
plt.title('Relationship between Gold Purity and Price')
plt.grid(True)
plt.show()
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
# Define the sigmoid function
def sigmoid(x, a, b):
return 1 / (1 + np.exp(-(a * x + b)))
# Define the gradient descent function for sigmoid
def gradient_descent_sigmoid(X, y, P, learning_rate, n_iterations):
m = len(y)
cost_history = np.zeros(n_iterations)
for i in range(n_iterations):
P = P - learning_rate * (1/m) * X.T.dot(sigmoid(X.dot(P), 1, 0) - y)
cost_history[i] = cost_function_sigmoid(X, y, P)
return P, cost_history
# Define the cost function for sigmoid
def cost_function_sigmoid(X, y, P):
m = len(y)
return -1 / m * np.sum(y * np.log(sigmoid(X.dot(P), 1, 0)) + (1 - y) * np.log(1 - sigmoid(X.dot(P), 1, 0)))
# Random data generation for classification
np.random.seed(42)
n_samples = 50
density = np.random.uniform(0.8, 2.0, n_samples)
threshold = 1.4
material = np.where(density > threshold, 1, 0)
# Creating the design matrix X for classification
X_class = np.column_stack((np.ones(n_samples), density))
# Creating the target vector y for classification
y_class = material.reshape(material.shape[0], 1)
# Initialize P for sigmoid classification
P_class = np.random.randn(2, 1)
# Setting the learning rate and number of iterations for sigmoid classification
learning_rate_class = 0.5
n_iterations_class = 1000000
# Performing gradient descent for sigmoid classification
P_final_class, cost_history_class = gradient_descent_sigmoid(X_class, y_class, P_class, learning_rate_class, n_iterations_class)
# Calculate the sigmoid classification curve
x_range_class = np.linspace(0.8, 2.0, 100)
y_pred_sigmoid_class = sigmoid(x_range_class, P_final_class[1], P_final_class[0])
# Creating the plot for sigmoid classification
plt.figure(figsize=(10, 6))
plt.scatter(density, material, label='Data')
plt.plot(x_range_class, y_pred_sigmoid_class, color='red', label='Fitted Sigmoid Classification')
plt.xlabel('Density')
plt.ylabel('Material (Metal: 1, Plastic: 0)')
plt.title('Classification Using Fitted Sigmoid Curve')
plt.legend()
plt.grid(True)
plt.show()
# Display the fitted parameters and cost history for sigmoid classification
print("Fitted Sigmoid Classification Parameters (a, b):", P_final_class)
plt.plot(range(n_iterations_class), cost_history_class)
plt.xlabel('Number of Iterations')
plt.ylabel('Cost')
plt.title('Cost History during Gradient Descent (Sigmoid Classification)')
plt.show()
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
# Random data generation
np.random.seed(42)
n_samples = 50
purity = np.random.rand(n_samples)
gold_price = 1000 + 500 * purity + np.random.normal(0, 50, n_samples) # Linear model
# Creating the data array
data = np.column_stack((purity, gold_price))
# Creating a Pandas DataFrame for the table
df = pd.DataFrame(data, columns=['Purity', 'Gold Price'])
# Define the linear function
def linear(x, a, b):
return a * x + b
# Define the gradient descent function
def gradient_descent(X, y, P, learning_rate, n_iterations):
m = len(y)
cost_history = np.zeros(n_iterations)
for i in range(n_iterations):
P = P - learning_rate * (1/m) * X.T.dot(X.dot(P) - y)
cost_history[i] = cost_function(X, y, P)
return P, cost_history
# Define the cost function
def cost_function(X, y, P):
m = len(y)
return 1 / (2 * m) * np.sum((X.dot(P) - y) ** 2)
# Creating the design matrix X
X = np.column_stack((np.ones(n_samples), purity))
# Creating the target vector y
y = gold_price.reshape(gold_price.shape[0], 1)
# Initialize P
P = np.random.randn(2, 1)
# Setting the learning rate and number of iterations
learning_rate = 0.1
n_iterations = 1000
# Performing gradient descent
P_final, cost_history = gradient_descent(X, y, P, learning_rate, n_iterations)
# Calculate the linear regression line
x_range = np.linspace(0, 1, 100)
y_pred = linear(x_range, P_final[1], P_final[0])
# Creating the plot
plt.figure(figsize=(10, 6))
plt.scatter(purity, gold_price, label='Data')
plt.plot(x_range, y_pred, color='red', label='Optimal Linear Regression')
plt.xlabel('Gold Purity')
plt.ylabel('Gold Price')
plt.title('Linear Relationship between Gold Purity and Price with Linear Regression')
plt.legend()
plt.grid(True)
plt.show()



